Figures on the same base and between the same parallels
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Figures on the same base and between the same parallels
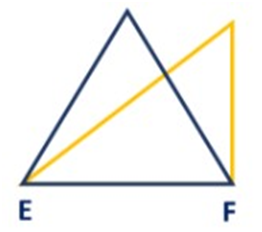
Two triangles with common base EF.
Two figures are between two parallels AB & CD but have different bases’ lengths.

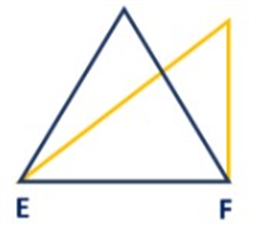
Two figures with common base XY and between two parallels XY & PQ.

“So, two figures are said to be on the same base and between the same parallels, if they have a common base (side) and the vertices (or the vertex) opposite to the common base of each figure lie on a line parallel to the base”. [As shown in the figure above]
Example: Choose which of the following figures lie on the same base and between the same parallels. For such a figure, write the common base and the two parallels.
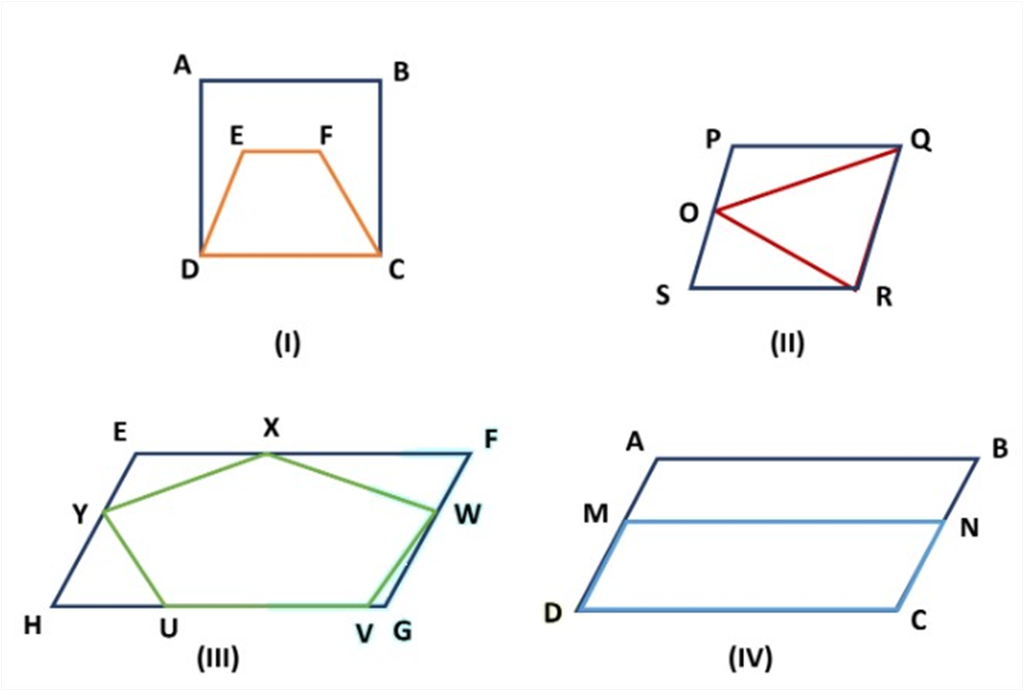
Solution:
I. Rectangle ABCD and trapezium EFCD are on the same base CD but they are not between the same parallels.
II. Parallelogram PQRS and ∆ ROQ are on the same base RQ and between the same parallel lines PS and QR.
III. Parallelogram EFGH and pentagon UVWXY are between the same parallel EF and HG but they are not on the same base.
IV. Parallelogram ABCD and parallelogram MNCD lie between the same parallels AB and CD and they have a common base CD.
RECTANGLE AREA AXIOM
If ABCD is a rectangular region such that AB = a units and BC = b units in length, then

CONGRUENT AREA AXIOM
Consider two ∆ ABC and ∆ DEF which are congruent to each other.

Now, we calculate the area of ∆ ABC, then we get
ar(∆ABC) = 1/2× base × height.
![]() × 3 cm × 4 cm.
× 3 cm × 4 cm.
= 3 cm × 2 cm.
= 6 cm2.
Also, we calculate the area of ∆ DEF, then we get
ar(∆DEF) = ![]() × base × height.
× base × height.
= ![]() × 3 cm × 4 cm.
× 3 cm × 4 cm.
= 3 cm × 2 cm.
= 6 cm2.
Here, we also see that the area of triangles ABC and DEF are equal.
Therefore, we conclude that if two figures are congruent with each other, they must have equal areas.
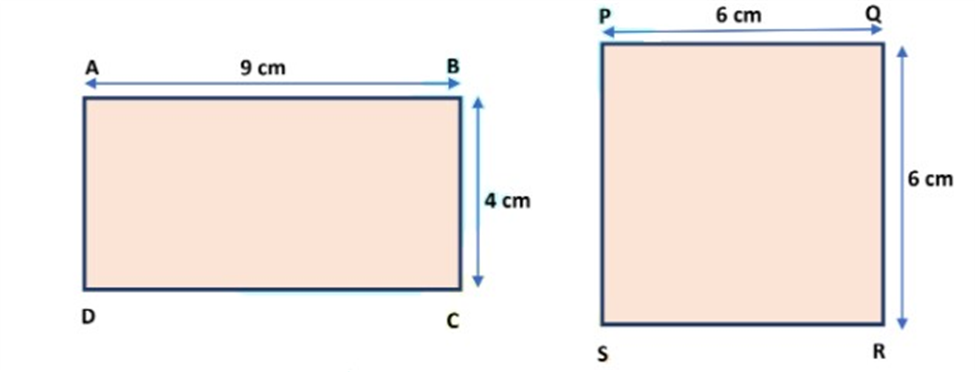
Now, consider a rectangle ABCD and square PQRS which are equal in area.

We calculate the area of rectangle ABCD, then we get ar(ABCD) = Length × Breath.
= 9 cm × 4 cm.
= 36 cm2
Also, we calculate the area of square PQRS, then we get
ar(PQRS) = Side × Side.
= 6 cm × 6 cm.
= 36 cm2.
Here, we see that areas of triangles ABC and DEF are equal. Rectangles ABCD and square PQRS are not congruent, but still, they have equal areas. Therefore, we can conclude that if two figures are congruent, they will have equal areas whereas, if two figures have equal areas, they need not be congruent with each other.
AREA MONOTONE AXIOM:
If R1, R2 are two polygonal regions such that R1 is a part of R2, then
ar(R1 ) ≤ ar(R2)
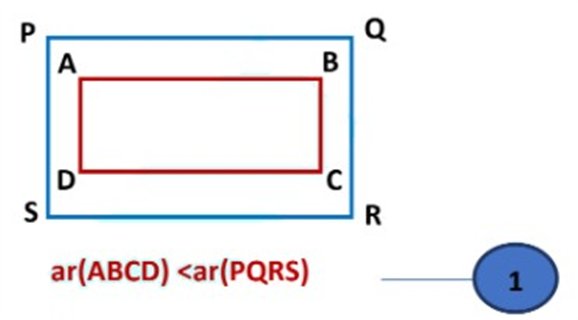
i.e. In the given figure region, ABCD is the part of region PQRS, which means

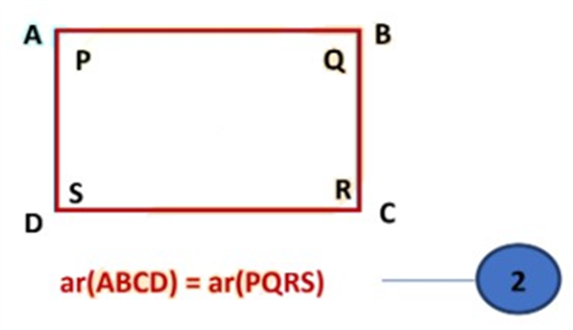
In the next figure (below) the region, the vertices A, B, C, D of parallelogram ABCD coincide with the vertices P, Q, R, S of the parallelogram PQRS.

The third possibility for figure ABCD and PQRS is

But in this case, ar(ABCD) >ar(PQRS) and PQRS is the part of ABCD which is not held by the statement of the axiom. So, this case shall not be considered.
AREA ADDITION AXIOM:
If a planer region formed by a figure T is made up of two non-overlapping planar regions formed by figures P and Q, then ar (T)=ar (P)+ar (Q).

In the figure above, ar(ABCD) = ar(∆ADB) + ar(∆BCD
Figures on the same base and between the same parallels
Chapter 9 - Areas of parallelograms and triangles
Figures on the same base and between the same parallels
Figures on the same base and between the same parallels
Two triangles with common base EF.
Two figures are between two parallels AB & CD but have different bases’ length.
Two figures with common base XY and between two parallels XY & PQ.
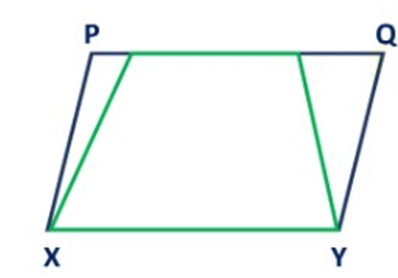
“So, two figures are said to be on the same base and between same parallels, if they have a common base (side) and the vertices (or the vertex) opposite to the common base of each figure lie on a line parallel to the base”. [As shown in the figure above]
Example: Choose which of the following figures lie on the same base and between the same parallels. For such a figure, write the common base and the two parallels.
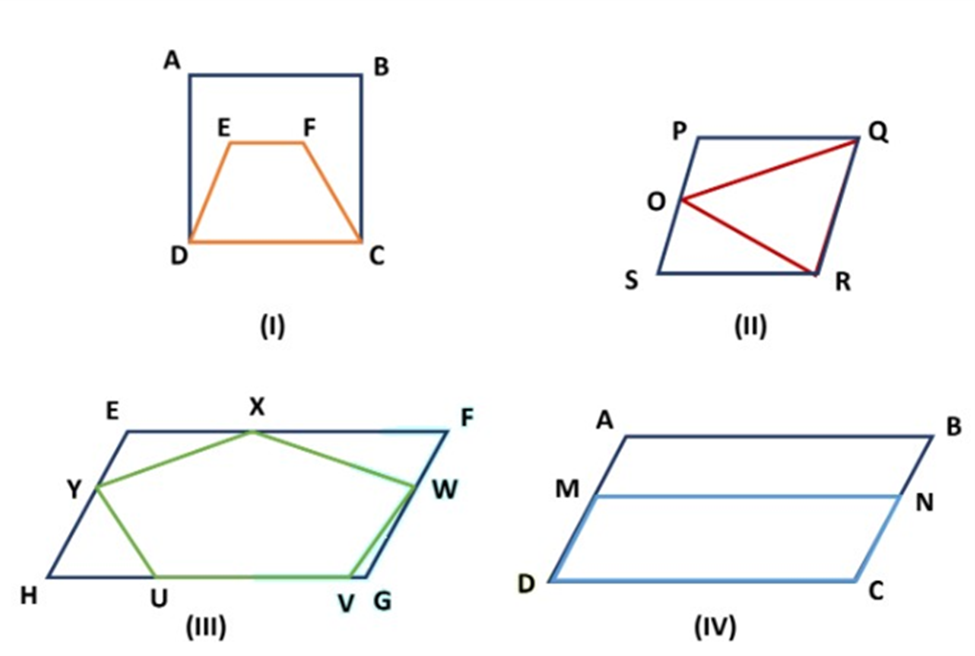
Solution:
I. Rectangle ABCD and trapezium EFCD are on the same base CD but they are not between the same parallels.
II. Parallelogram PQRS and ∆ ROQ are on the same base RQ and between the same parallel lines PS and QR.
III. Parallelogram EFGH and pentagon UVWXY are between the same parallel EF and HG but they are not on the same base.
IV. Parallelogram ABCD and parallelogram MNCD lie between the same parallels AB and CD and they have common base CD.
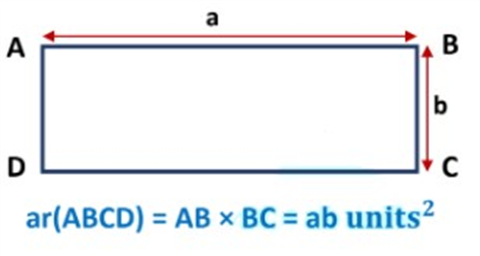
RECTANGLE AREA AXIOM
If ABCD is a rectangular region such that AB = a units and BC = b units in length, then
CONGRUENT AREA AXIOM
Consider two ∆ ABC and ∆ DEF which are congruent to each other.
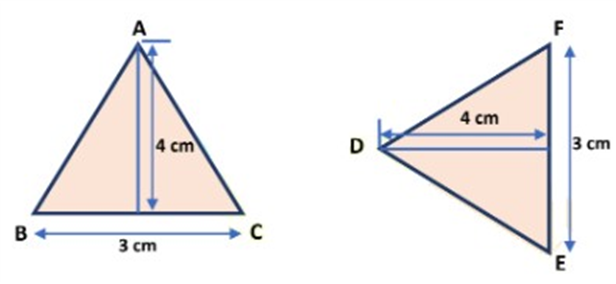
Now, we calculate the area of ∆ ABC, then we get
ar(∆ABC) = 1/2× base × height.
=  × 3 cm × 4 cm.
× 3 cm × 4 cm.
= 3 cm × 2 cm.
= 6 cm2.
Also, we calculate the area of ∆ DEF, then we get
ar(∆DEF) =  × base × height.
× base × height.
=  × 3 cm × 4 cm.
× 3 cm × 4 cm.
= 3 cm × 2 cm.
= 6 cm2.
Here, we also see that the area of triangles ABC and DEF are equal.
Therefore, we conclude that if two figures are congruent with each other, they must have equal areas.
Now, consider a rectangle ABCD and square PQRS which are equal in area.
We calculate the area of rectangle ABCD, then we get ar(ABCD) = Length × Breath.
= 9 cm × 4 cm.
= 36 cm2
Also, we calculate the area of square PQRS, then we get
ar(PQRS) = Side × Side.
= 6 cm × 6 cm.
= 36 cm2.
Here, we see that areas of triangles ABC and DEF are equal. Rectangles ABCD and square PQRS are not congruent, but still, they have equal areas. Therefore, we can conclude that if two figures are congruent, they will have equal areas whereas, if two figures have equal areas, they need not be congruent with each other.
AREA MONOTONE AXIOM:
If R1, R2 are two polygonal regions such that R1 is a part of R2, then
ar(R1 ) ≤ ar(R2)
i.e. In the given figure region, ABCD is the part of region PQRS, that means
In the next figure (below) the region, the vertices A, B, C, D of parallelogram ABCD coincide with the vertices P, Q, R, S of the parallelogram PQRS.
The third possibility for figure ABCD and PQRS is
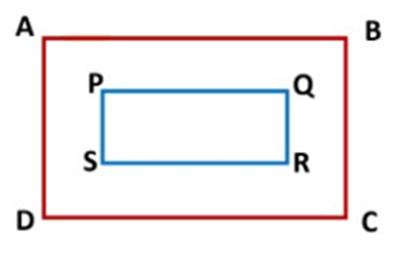
But in this case, ar(ABCD) >ar(PQRS) and PQRS is the part of ABCD which is not held by the statement of the axiom. So, this case shall not be considered.
AREA ADDITION AXIOM:
If a planer region formed by a figure T is made up of two non-overlapping planar regions formed by figures P and Q, then ar (T)=ar (P)+ar (Q).
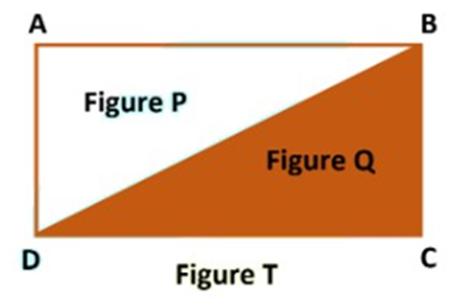
In the figure above, ar(ABCD) = ar(∆ADB) + ar(∆BCD)
Parallelograms on the same base and between the same parallels
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Parallelograms on the same base and between the same parallels
Parallelograms on the same base and between the same parallels are explained here in this article with the help of the theorem.
Theorem: - A parallelogram on the same base and between the same parallels are equal in area.
Proof:
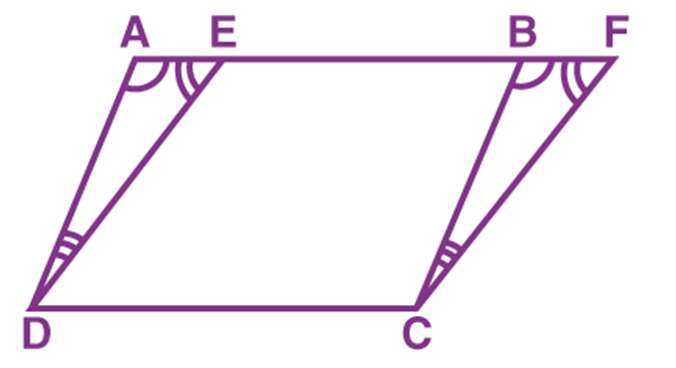
Consider two parallelograms ABCD and EFCD on the same base DC and the same parallels AF and DC, as shown in the figure.
To prove: ar (ABCD) = ar (EFCD)
It means that we need to prove the area of parallelogram ABCD is equal to the area of a parallelogram EFCD.
Consider the triangles ADE and BCF,
∠ DAE = ∠ CBF [Corresponding angles from AD || BC and transversal AF] …(1)
∠ AED = ∠ BFC [Corresponding angles from ED || FC and transversal AF] …(2)
By using the angle sum property of a triangle, we can write:
∠ ADE = ∠ BCF ….(3)
Also, from the opposite sides of a parallelogram ABCD, we can write:
AD = BC ….(4)
Using the equations (1), (3), and (4) and by Angle-Side-Angle (ASA) rule,
∆ ADE ≅ ∆ BCF
Therefore, the area of triangle ADE is equal to the area of a triangle BCF. (As congruent figures have equal area)
(i.e) ar (ADE) = ar (BCF) …(5)
Thus, the ar (ABCD) = ar (ADE) + ar (EDCB)
ar (ABCD) = ar (BCF) + ar (EDCB) (using equation (5))
ar (ABCD) = ar (EFCD)
Thus, the area of parallelogram ABCD is equal to the area of parallelogram EFCD.
Hence, a parallelogram on the same base and between the same parallels are equal in area, is proved.
Example - Now, let us solve the below problem with the help of the theorem.
Question: Consider a parallelogram ABCD and EFCD is a rectangle. Also, AL is perpendicular to DC.
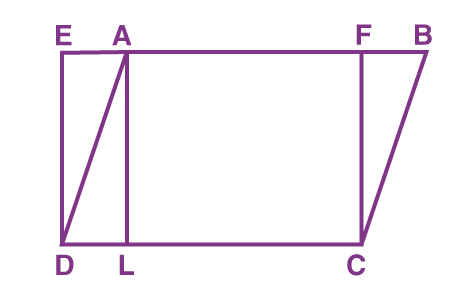
Prove that:
- ar (ABCD) = ar (EFCD)
- ar (ABCD) = DC × AL
Solution:
Given that ABCD is a parallelogram, and EFCD is a rectangle.
To prove : ar (ABCD) = ar (EFCD)
A rectangle is also a parallelogram, and by using the theorem “parallelogram on the same base and between the same parallels are equal in the area”, we can write
ar (ABCD) = ar (EFCD)
Hence proved.
To prove: ar (ABCD) = DC × AL
By using ar (ABCD) = ar (EFCD)
ar (ABCD) = DC × FC (As, the area of a rectangle = Length × Breadth) …(1)
Also given that AL ⊥ DC, we can say AFCL is also a rectangle.
Therefore, AL = FC …(2)
From (1) and (2), we can get ar (ABCD) = DC × AL
Hence, proved.
Practice Problems
Solve the following problems:
- The points P and Q lie on the sides DC and AD respectively of a parallelogram ABCD. Prove that ar (APB) = ar (BQC)
- In the figure given below, PQRS and ABRS are parallelograms. “X” is the point on the side BR.
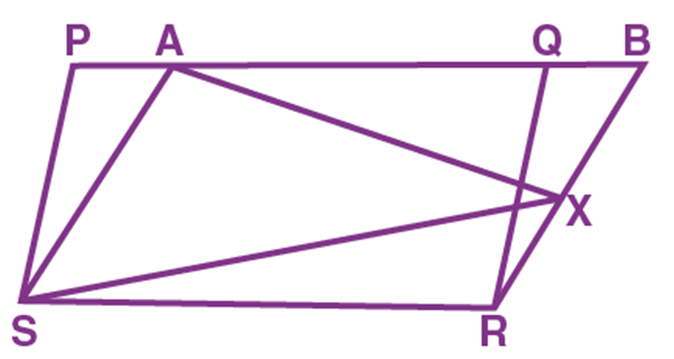
Prove that:
(1) ar (PQRS) = ar (ABRS)
(2) ar (AX S) = ½ ar (PQRS)
Parallelograms on the same base and between the same parallels
Parallelograms on the same base and between the same parallels
Parallelograms on the same base and between the same parallels are explained here in this article with the help of the theorem.
Theorem:
A parallelogram on the same base and between the same parallels are equal in area.
Proof:

Consider two parallelograms ABCD and EFCD on the same base DC and the same parallels AF and DC, as shown in the figure.
To prove: ar (ABCD) = ar (EFCD)
It means that we need to prove the area of parallelogram ABCD is equal to the area of a parallelogram EFCD.
Consider the triangles ADE and BCF,
∠ DAE = ∠ CBF [Corresponding angles from AD || BC and transversal AF] …(1)
∠ AED = ∠ BFC [Corresponding angles from ED || FC and transversal AF] …(2)
By using the angle sum property of a triangle, we can write:
∠ ADE = ∠ BCF ….(3)
Also, from the opposite sides of a parallelogram ABCD, we can write:
AD = BC ….(4)
Using the equations (1), (3), and (4) and by Angle-Side-Angle (ASA) rule,
∆ ADE ≅ ∆ BCF
Therefore, the area of triangle ADE is equal to the area of a triangle BCF. (As congruent figures have equal area)
(i.e) ar (ADE) = ar (BCF) …(5)
Thus, the ar (ABCD) = ar (ADE) + ar (EDCB)
ar (ABCD) = ar (BCF) + ar (EDCB) (using equation (5))
ar (ABCD) = ar (EFCD)
Thus, the area of parallelogram ABCD is equal to the area of parallelogram EFCD.
Hence, a parallelogram on the same base and between the same parallels are equal in area, is proved.
Example
Now, let us solve the below problem with the help of the theorem.
Question:
Consider a parallelogram ABCD and EFCD is a rectangle. Also, AL is perpendicular to DC.
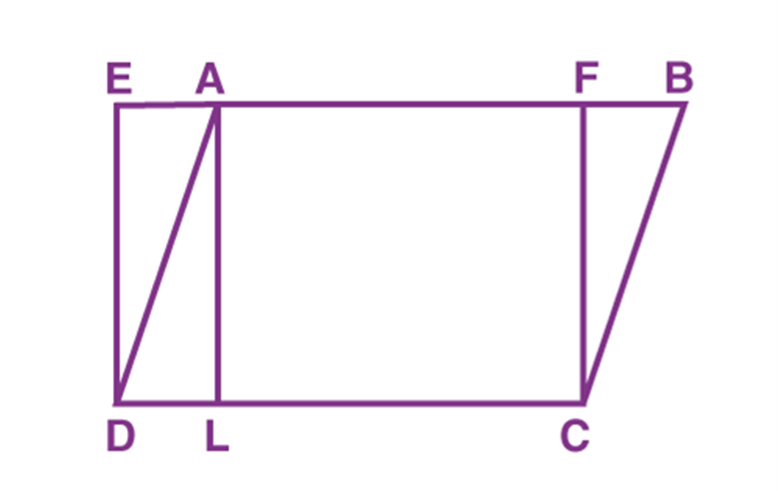
Prove that:
- ar (ABCD) = ar (EFCD)
- ar (ABCD) = DC × AL
Solution:
Given that ABCD is a parallelogram, and EFCD is a rectangle.
To prove : ar (ABCD) = ar (EFCD)
A rectangle is also a parallelogram, and by using the theorem “parallelogram on the same base and between the same parallels are equal in the area”, we can write
ar (ABCD) = ar (EFCD)
Hence proved.
To prove: ar (ABCD) = DC × AL
By using ar (ABCD) = ar (EFCD)
ar (ABCD) = DC × FC (As, the area of a rectangle = Length × Breadth) …(1)
Also given that AL ⊥ DC, we can say AFCL is also a rectangle.
Therefore, AL = FC …(2)
From (1) and (2), we can get
ar (ABCD) = DC × AL
Hence, proved.
Practice Problems
Solve the following problems:
- The point P and Q lie on the sides DC and AD respectively of a parallelogram ABCD. Prove that ar (APB) = ar (BQC)
- In the figure given below, PQRS and ABRS are parallelograms. “X” is the point on the side BR.
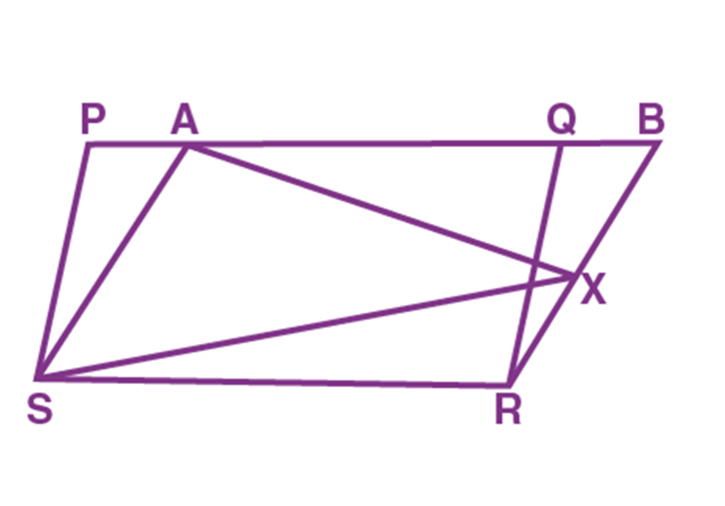
Prove that:
(1) ar (PQRS) = ar (ABRS)
(2) ar (AX S) = ½ ar (PQRS)
Triangles on the same base and between the same parallels
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Triangles on the same base and between the same parallels
Triangles on the same base and between the same parallels are explained here in this article using the theorem with a solved example.
Theorem: Two triangles on the same base and between the same parallels are equal in area.
Proof - Consider a parallelogram ABCD and AC be its diagonals as shown in the figure.
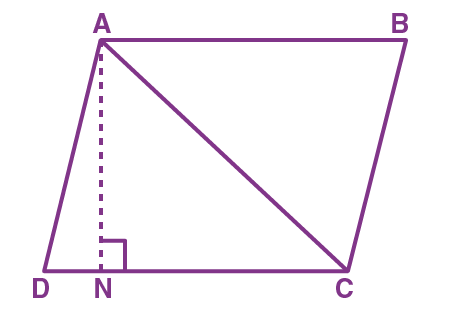
Assume that AN is perpendicular to DC.
We know that the diagonal of a parallelogram divides the parallelogram into two congruent triangles, we can write,
∆ ADC ≅ ∆ CBA
If the triangles are congruent, they have equal areas.
Thus, the area of a triangle ADC is equal to the area of a triangle CBA.
(i.e) ar (ADC) = ar (CBA)
Therefore, we can write
ar (ADC) = ½ ar (ABCD)
ar (ADC) = ½ (DC×AN)
Therefore, the area of the triangle = ½ × Base DC × Corresponding Altitude AN.
From the above formula, we can observe that two triangles with the same base (or equal bases) and equal areas will have equal corresponding altitudes.
In order to have an equal corresponding altitude, the triangles must lie between the same parallels.
Hence, two triangles on the same base and between the same parallels are equal in area.
The converse of this Theorem: Two triangles having the same base (or equal bases) and equal areas lie between the same parallels.
Example - Now, let us understand this theorem with the help of an example.
Question: Prove that the median of a triangle divides it into two triangles of equal areas.
Solution: Consider a triangle ABC and AD to be one of its diagonals.
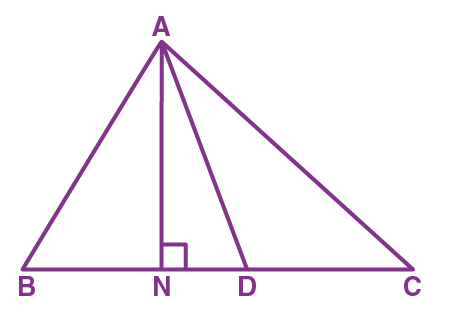
Now, we have to prove that,
ar (ABD) = ar (ACD).
Now, draw the line AN perpendicular to BC.
Therefore, the area of triangle ABD becomes,
ar(ABD) = ½ × base × altitude (of ∆ ABD)
In a triangle ABD, the base is BD and the altitude is AN.
Therefore, ar(ABD) = ½ (BD×AN)
As, BD = CD, the above mentioned equation can be written as:
ar(ABD) = ½ (CD×AN)
ar(ABD) = ½ × base × altitude (of ∆ ACD)
ar(ABD) = ar(ACD)
Hence, the median of a triangle divides it into two triangles of equal areas, which is proved.
Practice Problems
Solve the following problems.
- Prove that the diagonals of a parallelogram divide the parallelogram into four triangles of equal areas.
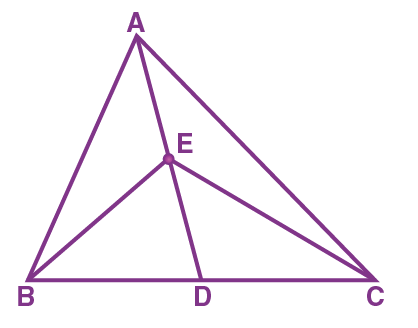
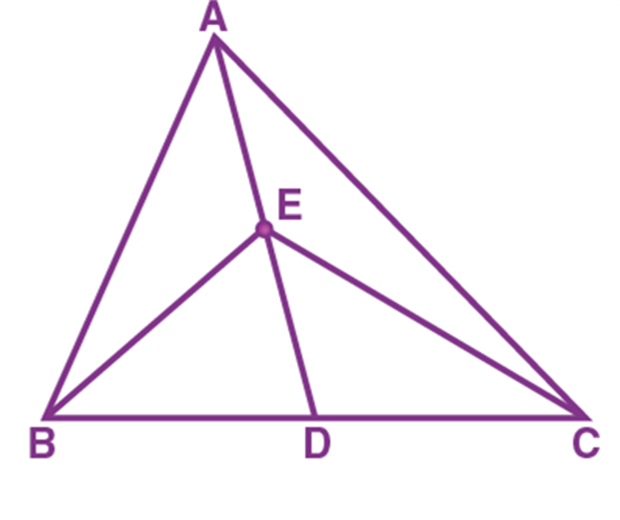
- E is the midpoint of median AD of a triangle ABC as shown in the figure. prove that ar (ABE) = ar (ACE).
Triangles on the same base and between the same parallels
Triangles on the same base and between the same parallels
Triangles on the same base and between the same parallels are explained here in this article using the theorem with a solved example.
Theorem:
Two triangles on the same base and between the same parallels are equal in area.
Proof
Consider a parallelogram ABCD and AC be its diagonals as shown in the figure.
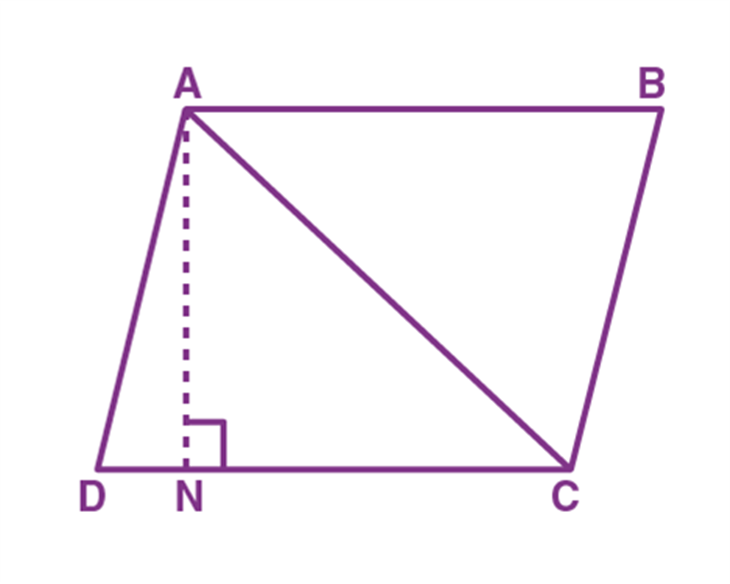
Assume that AN is perpendicular to DC.
We know that the diagonal of a parallelogram divides the parallelogram into two congruent triangles, we can write,
∆ ADC ≅ ∆ CBA
If the triangles are congruent, they have equal areas.
Thus, the area of triangle ADC is equal to the area of a triangle CBA.
(i.e) ar (ADC) = ar (CBA)
Therefore, we can write
ar (ADC) = ½ ar (ABCD)
ar (ADC) = ½ (DC×AN)
Therefore, the area of the triangle = ½ × Base DC × Corresponding Altitude AN.
From the above formula, we can observe that two triangles with the same base (or equal bases) and equal areas will have equal corresponding altitudes.
In order to have an equal corresponding altitude, the triangles must lie between the same parallels.
Hence, two triangles on the same base and between the same parallels are equal in area.
Converse of this Theorem:
Two triangles having the same base (or equal bases) and equal areas lie between the same parallels.
Example
Now, let us understand this theorem with the help of an example.
Question:
Prove that the median of a triangle divides it into two triangles of equal areas.
Solution:
Consider a triangle ABC and AD be the one of its diagonals.
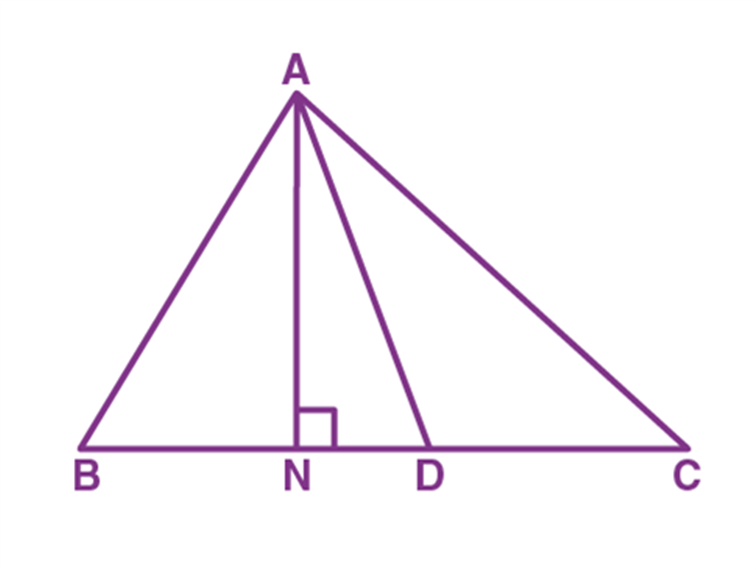
Now, we have to prove that,
ar (ABD) = ar (ACD).
Now, draw the line AN perpendicular to BC.
Therefore, the area of triangle ABD becomes,
ar(ABD) = ½ × base × altitude (of ∆ ABD)
In a triangle ABD, the base is BD and altitude is AN.
Therefore, ar(ABD) = ½ (BD×AN)
As, BD = CD, the above mentioned equation can be written as:
ar(ABD) = ½ (CD×AN)
ar(ABD) = ½ × base × altitude (of ∆ ACD)
ar(ABD) = ar(ACD)
Hence, the median of a triangle divides it into two triangles of equal areas, is proved.
Practice Problems
Solve the following problems.
- Prove that the diagonals of a parallelogram divides the parallelogram into four triangles of equal areas.
- E is the midpoint of median AD of a triangle ABC as shown in the figure. prove that ar (ABE) = ar (ACE).

 ABCD CLASSES
ABCD CLASSES
