1.Zeros of Polynomial
- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics
2.1 INTRODUCTION :
In earlier classes, we have learnt about polynomials in one variable, their degrees, factors, multiples and zeros (or roots). In this chapter, we will study about the geometrical representation of linear quadratic and cubic polynomials and geometrical meaning of their zeros. We will also study about the relationship between the zeros and coefficients of a polynomial. LCM and HCF of two or more polynomials, rational expressions, basic operation on polynomials and concept of square root of polynomials.



1. Solution of Two Linear Equations in Two Variables in Different Methods
- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics
3.1 INTRODUCTION
While solving the problems, in most cases, first we need to frame an equation. In this chapter, we learn how to frame and solve equations. There are given some methods to solve these equations. We will further study about word problems and application of simultaneous equations.
Equation: A statement in which two algebraic expressions are equal is known as equation.
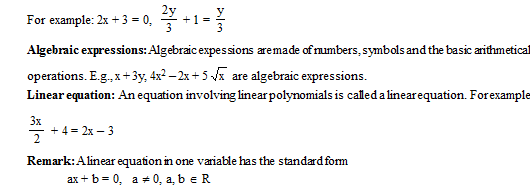
Solution (root) of a linear equation: The value of the variable which makes the two sides of the equation equal and satisfies the equation is called the solution of the equation.
Rules for solving an equation:
(i) The same number is added or subtracted to both sides of an equation, the resulting equation is equivalent to the first.
(ii) If both sides of an equation are multiplied by the same non-zero number the resulting equation is equivalent to the first.
Remark: Every linear equation in one variable has only one (unique) solution.
In this chapter we shall study about system of linear equation in two variables, solution of a system of linear equations in two variables.

3.3 algebraic methods of solving a pair of linear equations
There are four methods for solving a pair of linear equations
(i) Substitution method
(ii) Elimination method
(iii) Cross-multiplication method
(iv) Graphical Method

3.3.2 Elimination Method
Step–I: Obtain the two equations
Step–II: First multiply both the equations by some suitable non-zero constant to make the coefficient of one variable (either x or y) numerically equal.
Step–III: Add or subtract one equation from the other, then one variable gets eliminated.
Step–IV: Solve the equation in one variable.
Step–V: Substitute the value of x (or y) in any one of the given equations and find the value of another variable.
1.Solution of Quadratic Equation by Factorisation
- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics


1.Arithmetic Progression Basics
- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics
INTRODUCTION :
In practical life, we must have observed many things follow a certain pattern, such as the petals of a sunflower, the holes of a honeycomb, the grains on a maize cob, the spirals on a pineapple on a pipe cone.
In our day-to-day life we see patterns of geometric figures on clothes, picture, posters. They make the learners motivated to form such new pattern.
For example,

Likewise number patterns are also faced by learners. In their study, number pattern play an important role in the field of mathematics.
Ex. (i) 2, 4, 6, 8, 10 then next number is 12.
![]()
Idea on A.P. was given by mathematician Carl Friedrich Gauss, who was a young boy, stunned his teacher by adding up 1 + 2 + 3 + ........+ 99 + 100 within a few minutes. Here’s how he did it:
He realised that adding the first and last numbers, 1 and 100, gives, 101; and adding the second and second last numbers, 2 and 99, gives 101, as well as 3 + 98 = 101 so on .
Thus he concluded that there are 50 sets of 101. So the series is :
50(1 + 100) = 5050.
In this chapter, you will study only Arithmetic Progression (A.P.) and Geometric Progression (G.P.).
Arithmetic progression (A.P.) :
A sequence is called an arithmetic progression, if the difference of a term and previous term is always same.
The difference is called the common difference of arithmetic progression.
The sequence is called an arithmetic progression (A.P.), if d = x2 – x1 = x3 – x2 = xn – xn – 1 = ...........
It is a sequence whose terms decrease or increase by a fix/constant number. This constant number is called common difference of A.P. and it generally denoted by ‘d’.
[d = an+1–an]
Illustration 1
Find the A.P. whose 1st term is 2 & common difference is 3.
Solution
Given : First term (a) = 2 & Common difference (d) = 3.
A.P. is 2, 5, 8, 11, 14,.......
Illustration 2
Show that the sequence on defined by an = 4n + 5 is an A.P. Also find its common difference.
Solution
a1 = 9, a2 = 13, a3 = 17,....... in A.P.
We have an = 4n + 5 .....(i)
Replacing n by (n + 1) we get
an +1 = 4(n + 1) + 5 = 4n + 4 + 5
an+1 = 4n + 9 .....(ii)
d = an+1 – an ⟹ d = (4n + 9) – (4n + 5) ⟹ d = 4
Remarks:
(i) The common difference ‘d’ should be independent of n.
Properties of Arithmetic Progression :
Property–1: If a constant is added to or subtracted from each term of an AP, then the resulting sequence is also an AP with the same common difference.
Property–2: If each term of a given AP is multiplied or divided by a non-zero constant k, then the resulting sequence is also an AP with common difference kd or d/k respectively. Where d is the common difference of the given AP.
Property–3: In a finite AP the sum of the terms equidistant from the beginning and end is always same and is equal to the sum of first and last term i.e. ak + an – (k – 1) = a1 + an For all k = 1, 2, 3........(n – 1)
Property–4: Three numbers a, b, c are in AP if 2b = a + c
Property–5: A sequence is an AP if its nth term is a linear expression in n i.e. an = An + B where A, B are constants. In such a case the coefficient of n in an is the common difference of the AP.
Property–6: A sequence is an AP if the sum of its first n terms is of the form An2 + Bn where A, B are constants independent of n. In such a cases the common difference is 2A. i.e. 2 times the coefficient of n2.
Property–7: If the terms of an AP are chosen at regular intervals then they form an AP.
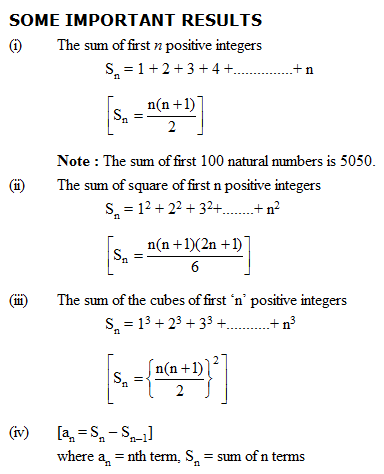
2.Zeros and Coefficients of Polynomial – 1
- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics


Method for finding HCF of the given polynomials :
Step 1 : Express each polynomial as a product of powers of irreducible factors which also requires the numerical factors to be expressed as the product of the powers of primes.
Step 2 : If there is no common factor then HCF is 1 and if there are common irreducible factors, we find the least exponent of these irreducible factors in the factorized form of the given polynomials.
Step 3 : Raise the common irreducible factors to the smallest or the least exponents found in step 2 and take their product to get the HCF.
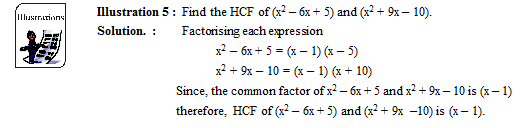
Geometric representation of different possibilities of solutions/inconsistency?
- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics
3.3 algebraic methods of solving a pair of linear equations
There are four methods for solving a pair of linear equations
(i) Substitution method
(ii) Elimination method
(iii) Cross-multiplication method
(iv) Graphical Method

3.3.2 Elimination Method
Step–I: Obtain the two equations
Step–II: First multiply both the equations by some suitable non-zero constant to make the coefficient of one variable (either x or y) numerically equal.
Step–III: Add or subtract one equation from the other, then one variable gets eliminated.
Step–IV: Solve the equation in one variable.
Step–V: Substitute the value of x (or y) in any one of the given equations and find the value of another variable.


3.3.4 Graphical Method:
In graphical method, we draw the graph of both equations using same pair of horizontal and vertical lines called X-axis and Y-axis respectively. Coordinates of the point(s) of intersection of the two lines is/are the solution.
Nature of solutions:
When we try of solve a pair of equations we could arrive at three possible results. They are, having
(a) a unique solution
(b) an infinite number of solutions
(c) no solution

Algebraic conditions for number of solutions?
- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics
3.3 algebraic methods of solving a pair of linear equations
There are four methods for solving a pair of linear equations
(i) Substitution method
(ii) Elimination method
(iii) Cross-multiplication method
(iv) Graphical Method

3.3.2 Elimination Method
Step–I: Obtain the two equations
Step–II: First multiply both the equations by some suitable non-zero constant to make the coefficient of one variable (either x or y) numerically equal.
Step–III: Add or subtract one equation from the other, then one variable gets eliminated.
Step–IV: Solve the equation in one variable.
Step–V: Substitute the value of x (or y) in any one of the given equations and find the value of another variable.


3.3.4 Graphical Method:
In graphical method, we draw the graph of both equations using same pair of horizontal and vertical lines called X-axis and Y-axis respectively. Coordinates of the point(s) of intersection of the two lines is/are the solution.
Nature of solutions:
When we try of solve a pair of equations we could arrive at three possible results. They are, having
(a) a unique solution
(b) an infinite number of solutions
(c) no solution

Solution of a pair of linear equations in two variables algebraically - by substitution, by elimination and by cross multiplication method?
- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics
3.6 Solution of a system of a pair of equations reducible to the system of a pair of linear equations in two variables
By using the suitable substitution or simplification first we convert the given system into the system of a pair of linear equations in two variables. Then after using any algebraic or graphical method we solve the system.
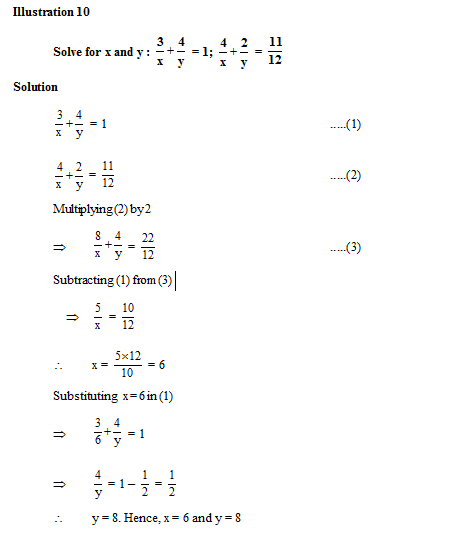
3.Determination of Types of Roots
- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics

Relationship between discriminant and nature of roots?
- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics



 Carrier Point
Carrier Point
