1. Electrostatic Potential
- Books Name
- Physics by Anshu Physics Book
- Publication
- Madhava Publications
- Course
- CBSE Class 12
- Subject
- Physics
Electrostatic Potential
Introduction
The concept of potential can only be understood only when you first understand conservative forces. As we can define potential with only those forces that are conservative in nature. For example, we have the gravitational potential for gravitational forces, and electrostatic potential for electrostatic ( Coulomb’s ) force, as these forces are conservative forces. Have anyone heard of frictional potential or drag potential?. There is no way we can have these potentials as frictional forces and drag forces are not conservative.
Now the next question is what exactly is a conservative force and how do we define it? Let's start it.
Conservative forces
There are many forms of energy: light energy, heat energy, sound energy, potential energy, kinetic energy, chemical energy etc.
But in mechanics, we define mechanical energy. Mechanical energy basically is the sum of potential energy and kinetic energy.
In mechanics when we say that total energy must remain the same; that is we are referring to the mechanical energy of the system
We say that under the effect of conservative forces the mechanical energy of the isolated system remains conserved.
Significance of conservative forces
The work done is independent of the path taken.

Suppose we have two points A and B, there can be many ways to reach B from A. The three possible paths are shown in the figure. Suppose the work done in reaching B from A via path 1 is W1 and similarly, we have W2 and W3 as work done for paths 2 and 3 respectively. So If the force would be conservative then W1=W2=W3.
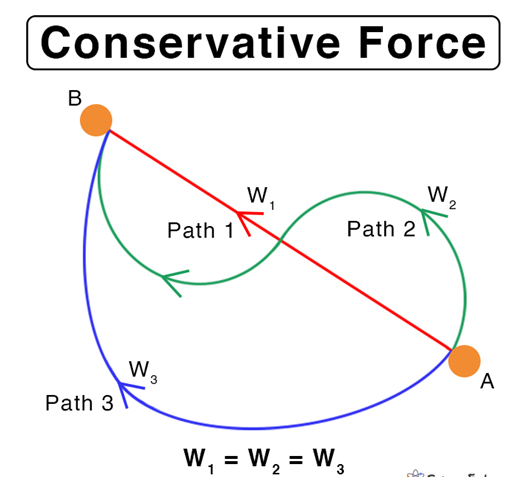
- Under conservative forces, the mechanical energy remains conserved.
If a body is subjected to conservative force and if its kinetic energy increases by some amount, its potential energy will decrease by the same amount to keep the total mechanical energy constant.
Let us try to understand this with the help of an example

- Suppose we have a body of mass m, kept at height H. At this point, the body possesses potential energy “mgH”. Suppose you drop that object and it starts coming down.
- Now which force will be acting on this object falling down? Gravitational force. Agree? From our discussion, we know the gravitational force is a conservative force.
- So due to gravity, there will be a downward force on the object, so there is acceleration in the downward direction too. We call this acceleration “acceleration due to gravity g “.
- So Due to acceleration in the downward direction, the speed of the object increases as it falls down and hence the Kinetic energy of the particle also increases.
- But Since the gravitational force is a conservative force, mechanical energy under this force must be constant so as Kinetic energy increases, its potential energy decreases by the same amount.
- At the lowest position, just before hitting the surface it will have maximum kinetic energy and have velocity say “V” and potential energy will be zero, as all of the Potential energy gets converted into Kinetic energy.
mgH= (½)mV^2
By the above equation, we can find the maximum velocity attained by the object of mass “m” when it is dropped from height “H”.
The above example is to demonstrate how the energy remains conserved in conservative force and what is conservative force?
Now we can move further. Our next discussion is about Potential energy.
Potential energy
When we do some work against the conservative force the work we do gets converted into the potential energy of the body.
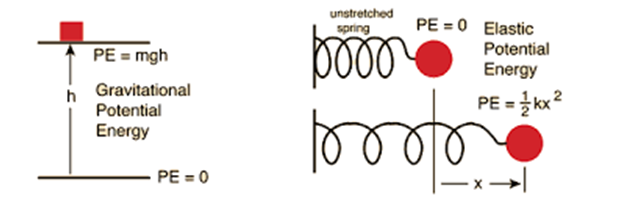
Example
- lifting an object to a height “H” against gravitational force stores potential energy of “mgH”.
- Compressing or expanding a spring by distance “x” introduces potential energy of (½)kx^2 In the spring of spring constant.
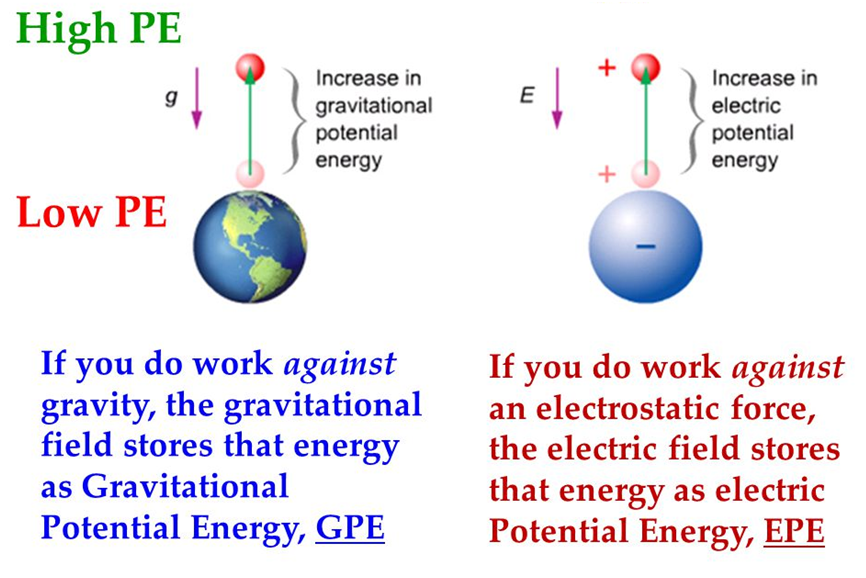
The way we have gravitational P.E we have electric potential energy as well.
Electrostatic potential energy.
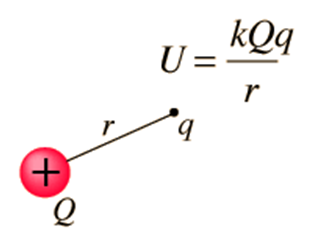
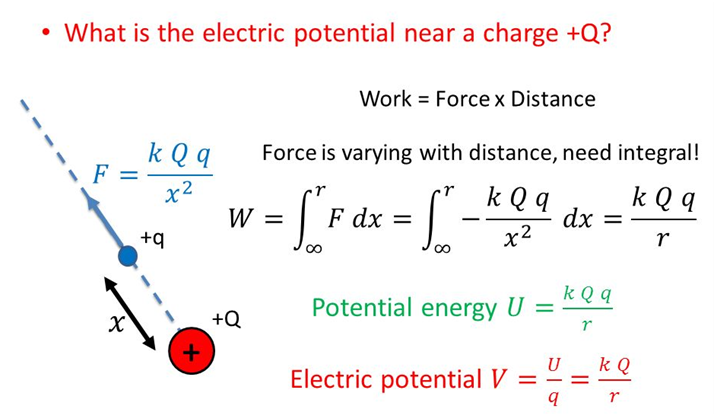
Suppose we have a charge Q placed at the origin. This Charge will have an electric field E around it. Now imagine we have a test charge “q” and we have to bring the test charge from infinity to Point R which is at distance r from the Q. Imagine both charges are of the same sign (Say positive).
Now while bringing the test charge “q” at point R, we have to work against the repulsive force due to charge Q as both are positive signs.

Assumptions:
- The test charge q is so small that it does not disturb the original configuration, here charge Q at the origin.
- We assume that we are bringing the test charge without acceleration, with constant speed so the external force just balances the repulsive force due to Q.
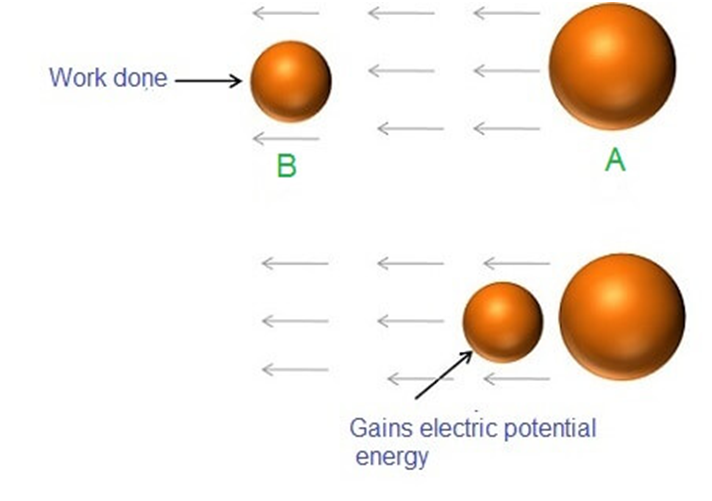
Points to be considered here:
- The external force must be in the opposite direction to the electrostatic repulsion force.
- The work done by an external force is negative to the work done by the electric force.
- If an external force is removed, the electric force will take charge and push the test charge q away and thus it will get some kinetic energy.
- The gain in kinetic energy after the removal of external force happens at the cost of loss of potential energy.
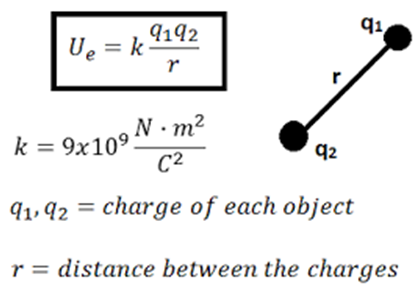
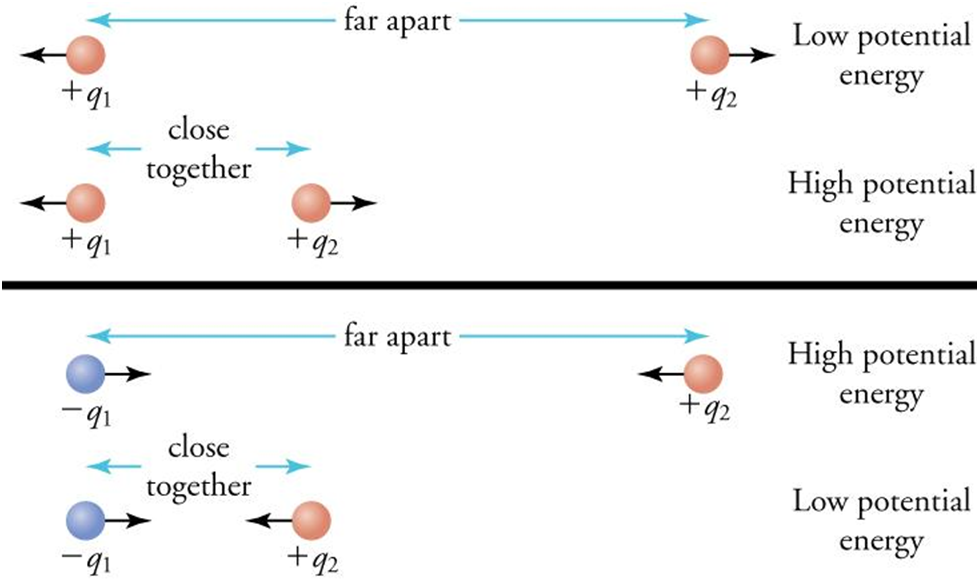
So we have discussed potential energy due to two charges Q and q separated by a distance “r”.
We notice here that electric potential energy and electric potential are proportional to charge “q” and inversely proportional to distance “r”.
I can surely say that at this point you might be wondering what is the difference between electric potential energy and electric potential.
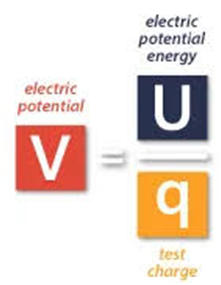
Electric potential energy is the work done in bringing the charge from infinity to a point in the electrostatic field of a charge.
The Unit of Electric potential energy is the same as work done and which is Joules. It is a scalar quantity.
Electric Potential
Electric potential is the work done per unit charge in order to bring that charge from infinity to a point in the electrostatic field.
Electric potential is referred to as Voltage and it is a scalar quantity.
Now let’s try to understand the electric potential difference
Electric Potential difference
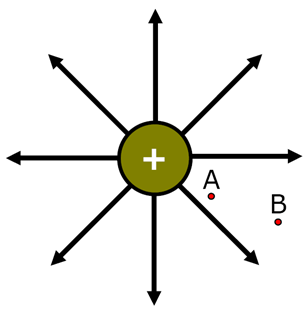
Imagine we have a charge Q. In the figure above you can see two points A and B. A is nearer to charge and B is father to charge. As we know Potential is inversely proportional to “r”. So we can conclude that A is at the higher potential here and B is at the lower potential. The difference in the Potential of A and B is called the Potential difference between A and B.
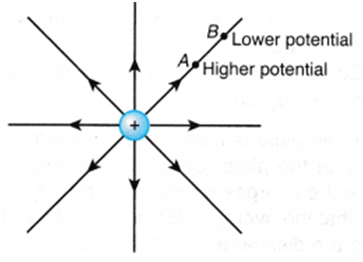
Suppose we have two points A and B at a distance of r1 and r2 from the charge Q. Then the potential difference between A and B will be given as
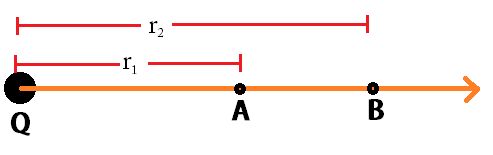
Va - Vb = K Q( (1/r1)- (1/r2))
S.I. unit of potential difference is the same as potential.
So In the discussion so far, I have tried to give you a detailed explanation of conservative force, the origin of the potential concept. We have discussed Electric potential energy, Electric Potential and its difference in quite a descriptive manner with illustrations of the diagrams.
Electric potential due to multiple charges: Superposition principle.
Like electric force and electric field, Electric potential also follows the principle of superposition. The only difference is that electric potential is scalar, therefore the Electric potential due to multiple charges at a point is simply the algebraic sum of the electric potential due to all individual charges.
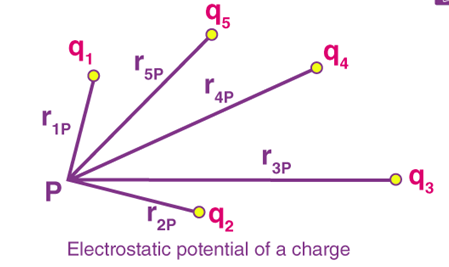
Suppose we have three charges Q1, Q2, Q3 which is at distance r1, r2, r3 respectively from a point P and we wish to find electric potential due to these charges at that point; Electric potential due to three charges will be simply the sum due to individual charges Like shown in the figure.
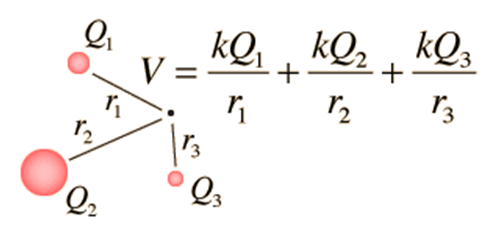
Electric potential due to Electric dipole.
In the previous chapter, we have discussed the Electric field due to electric dipoles at axial and equatorial positions.
In this section, we will discuss the electric potential at axial and equatorial positions.
Be assured! This is much easier than finding an Electric field as electric potential is a scalar quantity, unlike an electric field which is a vector quantity.
So we can do an algebraic sum in this case, rather than doing vector addition as in the case of electric fields due to dipoles.
Axial position: Suppose we have an electric dipole with charge
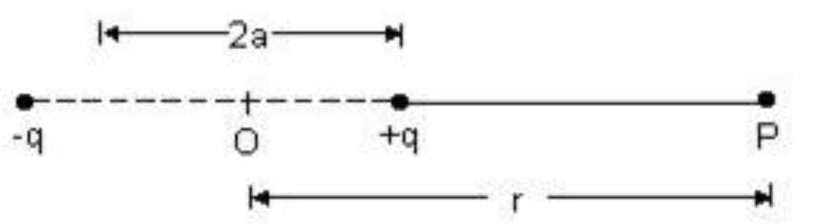
Potential at P will be an algebraic sum due to potential due to +q and -q charges which are at distance (r+a) and (r-a) respectively.
V at P = V(+q) (potential due to +q) + V(-q)(potential due to -q) = V(+q)+V(-q)

For r >> a, we can neglect ‘a’ in the denominator.
Then V is proportional to the square of the distance between them.
Equatorial Position:
Now suppose we wish to find the electric potential at the equatorial position due to the electric dipole.
Again Potential at P will be an algebraic sum due to potential due to +q and -q charges which are at distance (r+a) and (r-a) respectively.
V at P = V(+q) (potential due to +q) + V(-q)(potential due to -q) = V(+q)+V(-q)
Now we know that Electric potential is directly proportional to the magnitude of charge and inversely proportional to distance.
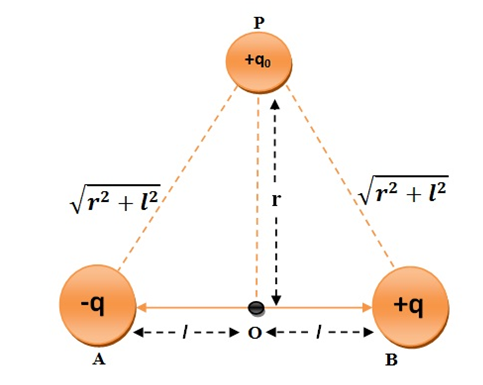
If you closely look at point P you will notice that the distance of P from either charge is the same and also the magnitude of the charges in the dipole is the same.
We can conclude from above that magnitude of potential due to
+q and -q is the same at P, but since one will be positive and the other to be negative so they will cancel each other out. The net electric potential due to the electric dipole at the equatorial position is zero.
Equipotential Surface.
- The surface at which the potential has a constant value is called the equipotential surface.
- The work done in moving a charge on an equipotential surface is zero because the potential at every point of the equipotential surface is the same as work done = charge * Potential difference, Since the potential difference is zero at the equipotential surface W=0
- For any charge configuration, the equipotential surface through a point is normal to the electric field at that point. In other words, we can say that electric field lines are perpendicular to the equipotential surface.
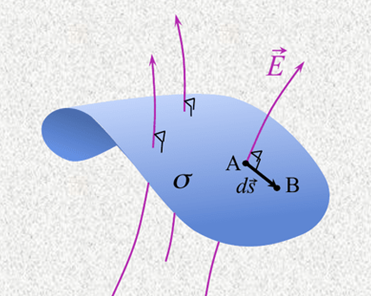
- The equipotential surfaces of a single point charge are concentric spherical surfaces centered at the charge
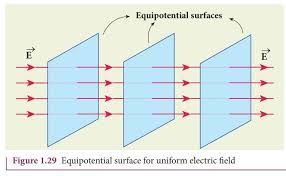
- Equipotential surfaces due to the uniform electric field are planes normal to the direction of the electric field.
- Equipotential surfaces due to electric dipole are also spheres perpendicular to electric field lines as shown in the figure below.
You will notice that the equipotential surfaces are neat to each other in between the charges and are farther on the other side.
This is because there are more electric field lines are more between the charges.
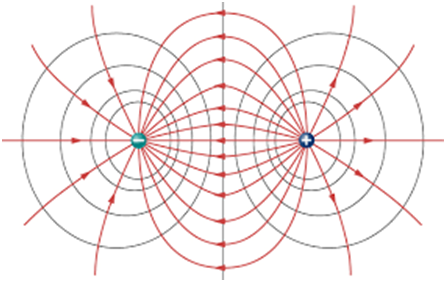
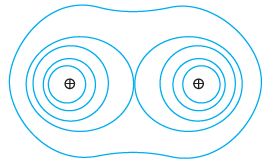
- Equipotential surface due to two similar charges ( say both positive) will also be a concentric sphere but in this case, equipotential surfaces are far from each other in between the charges and near to end on the other side. The reason is the same again as the electric field in between similar charges is less in between the similar charges.
- Equipotential surface due to two similar charges ( say both positive) will also be a concentric sphere but in this case, equipotential surfaces are far from each other in between the charges and near to end on the other side. The reason is the same again as the electric field in between similar charges is less in between the similar charges.
Relation between Electric field and electric potential
The concept of Electric field and Electric potential is introduced to understand and visualize how charges which are kept at a distance exert force on each other without any physical contact. But Electric field is a vector quantity and the electric potential is a scalar quantity and hence much simpler to deal with.
So there must be some connection between electric field and electric potential.
When V is given and E has to find out we will use the following relation.
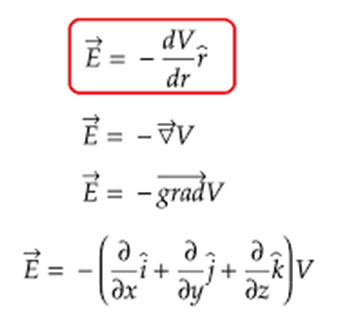
When E is given and a potential difference is to be found out, we will use the following relation.

1. Electrostatic Potential
- Books Name
- Physics Book Part l and ll
- Publication
- Grow Career Publication
- Course
- CBSE Class 12
- Subject
- Physics
Chapter 2: Electrostatic Potential and Capacitance

Electrostatic Potential
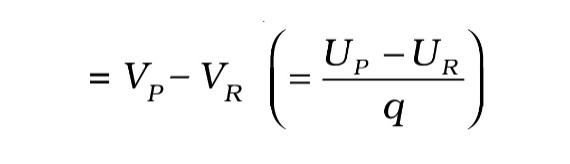
We define potential energy of a test charge q in terms of the work done on the charge q. This work is obviously proportional to q, since the force at any point is qE, where E is the electric field at that point due to the given charge configuration. It is, therefore, convenient to divide the work by the amount of charge q, so that the resulting quantity is independent of q. In other words, work done per unit test charge is characteristic of the electric field associated with the charge configuration
POTENTIAL DUE TO A POINT CHARGE
Take Q to be positive. We wish to determine the potential at any point P with position vector r from the origin. For that we must calculate the work done in bringing a unit positive test charge from infinity to the point P. For Q > 0, the work done against the repulsive force on the test charge is positive.
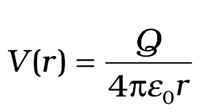
Potential due to an electric dipole
What is the electric potential due to an electric dipole at an equatorial point? Zero, as potential on equatorial point, due to charges of electric dipole, are equal in magnitude but opposite in nature and hence their resultant is zero.
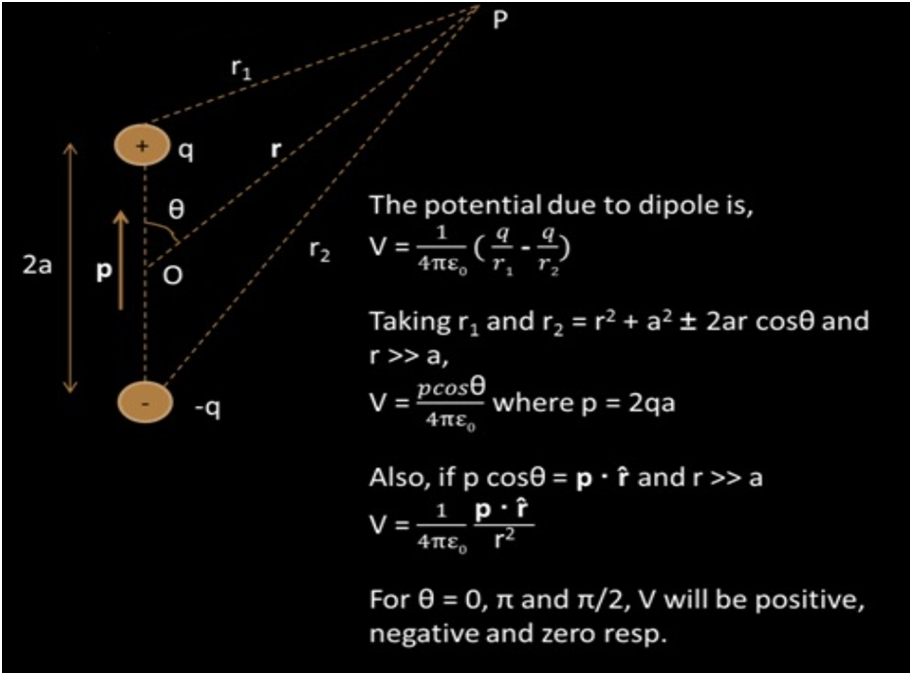
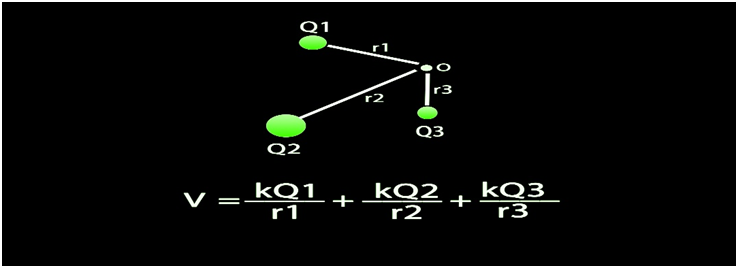
Potential due to system charges
derive an expression for the electric field at a point due to a system of n point charges. When there is a group of point charges say q1, q2, q3,….qn is kept at a distance r1, r2, r3,……rn, we can get the electrostatic potential at any particular point.
Equipotential surface.
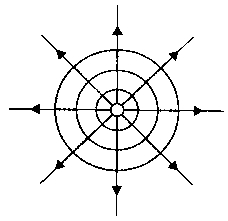
If the points in an electric field are all at the same electric potential, then they are known as the equipotential points. If these points are connected by a line or a curve, it is known as an equipotential line. If such points lie on a surface, it is called an equipotential surface.
Work Done in Equipotential Surface
The work done in moving a charge between two points in an equipotential surface is zero. Then the work done in moving the charge is given by
W = q0(VA –VB)
As VA – VB is equal to zero, the total work done is W = 0.
2. Potential energy
- Books Name
- Physics by Anshu Physics Book
- Publication
- Madhava Publications
- Course
- CBSE Class 12
- Subject
- Physics
Electric potential energy is due to the system of charges.
When we assemble a charge distribution, we need to do some work in assembling the charges. The work done by the external force to assemble the charge is stored in the system of charges as Potential energy of the system of charges.
- Suppose we have to make an assembly of a few charges. We can do this by putting charges at their respective position one by one.
- The work done in bringing the first charge Q1 from infinity and placing it at its respective position is zero as there is no other charge present to exert any force on the first charge. Work done for placing the first charge (W1=0) is zero.
W1=0
- Now when we bring the second charge from infinity in the presence of the first charge, the external force has to do some work against the electrostatic repulsive force of the first charge.
Therefore, W2( work done in placing 2nd charge )= U12( potential energy of first and second charge) = KQ1*Q2/ r12
W2= KQ1*Q2/r12, where r12 is the distance between r1 and r2.
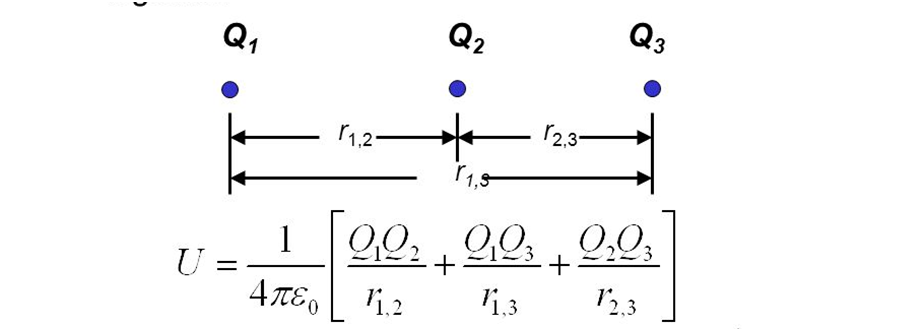
- Now if we wish to bring the third charge Q3 from infinity to its respective position, an external force has to do work against the electrostatic repulsion of both Q1 and Q2.
Therefore work done by the external force in bringing the charge
Q3= W3= U13+U23 = KQ1*Q3/r13 + KQ2*Q3/r23
- So the Potential energy stored in the system of charge is the total work done in assembling three charges that will be
Potential energy W= W1+ W2+ W3
= 0 + K*Q1*Q2/r12 + K*Q1*Q3/r13+ K*Q2*Q3/r23
- Now for a system of four charges, the total potential energy will be the work done to bring all four charges together.
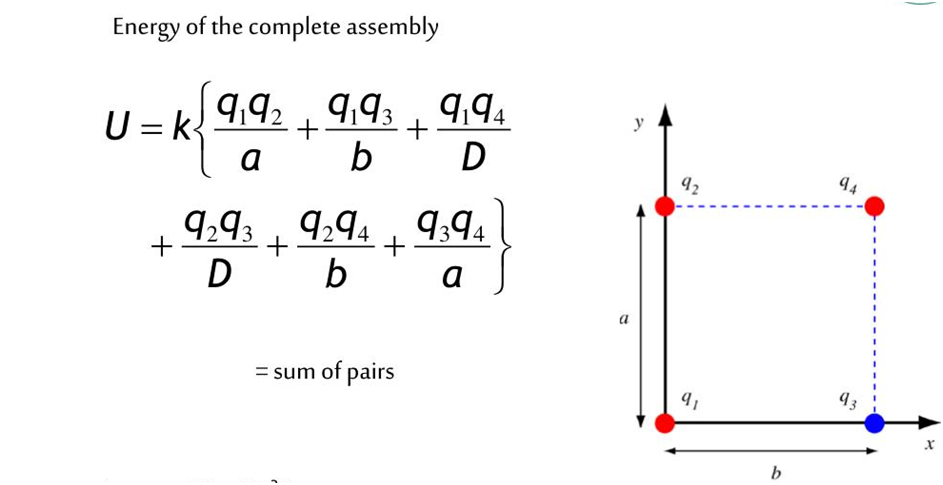
In the above example, I have shown the potential energy for a system of four charges placed at the corner of the square of the side “a” and diagonal “D”.
Electric Potential energy in the external Electric field.
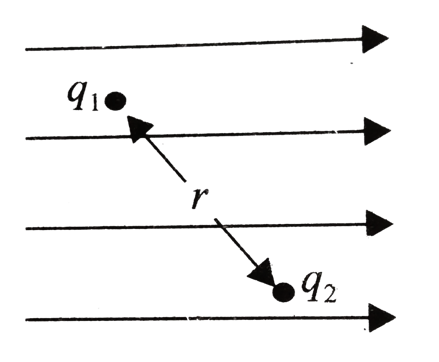
Suppose we have two charges q1 and q2 placed in an external electric field at positions r1 and r2 with respect to some origin. These charges are separated by distance ‘rd’
- Now suppose that the electric potential at the position of q1 is V(r1) due to external field E. So work done in placing the charge q1 at r1 in the presence of external field E will be q1(Vr1)
- The electric potential at the position of q2 is V(r2) due to external field E. So the work done in placing the charge at r2 in the presence of external electric field E is q2(Vr2)
- But in the case of the second charge, there will be influence due to charge q1 also. We need to bring q2 in the presence of both E and q1. So work done by the external force in bringing the charge q2 in presence of q1 at a separation ‘rd’ is = Kq1q2/rd
Therefore potential energy due to charges placed in the external electric field will be as shown below.
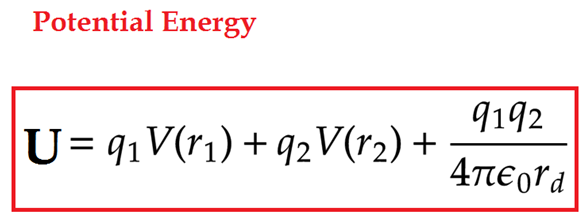
The potential energy of a dipole in an external electric field.
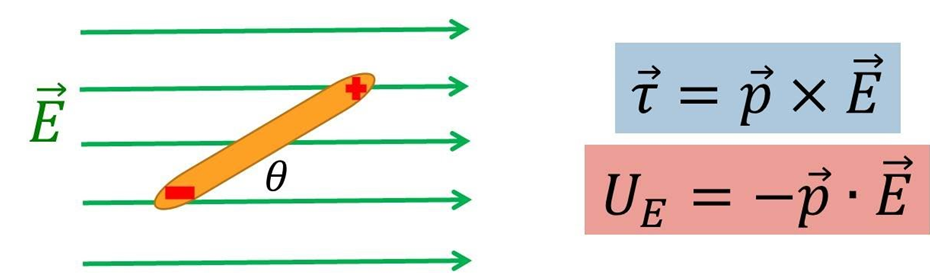
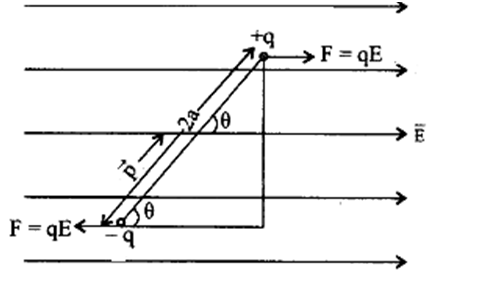
When we place an electric dipole in an external electric field, the charges will experience an electrostatic force qE. The forces on either charge of the electric dipole are equal in magnitude but opposite in direction.
The direction of the force will be in the direction of E for the positive charge and opposite to E for the negative charge.
Since their magnitudes are the same, these forces cancel each other. So there will be no translational motion in the electric dipole when placed in a uniform external field.
But they do experience a torque. As torque is the moment of force.
We define torque= as force* perpendicular distance between the forces.

When we try to rotate the electric dipole in an external field, it requires work done by some external force, and this work gets converted into the potential energy of the dipole of dipole moment P placed in an external uniform electric field.
Electrostatic of conductors
The conductor contains mobile charge carriers. In metallic conductors these charge carriers are electrons. The electrons from the valence shell of the atom of the metal behave like free electrons inside the metal and therefore conduct electricity. These free charge carriers form a kind of ‘gas’, they collide with each other and with the ions and move randomly in all directions. In the presence of an external field, they move and drift opposite to the direction of the field. The positive ions are made up of nuclei and bound electrons and remain held at fixed positions.
Properties regarding electrostatics of the conductors:
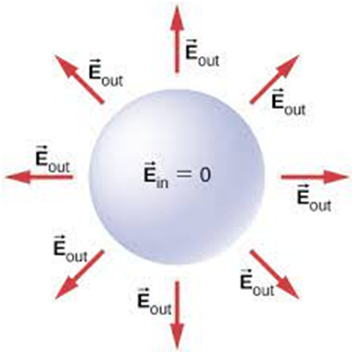
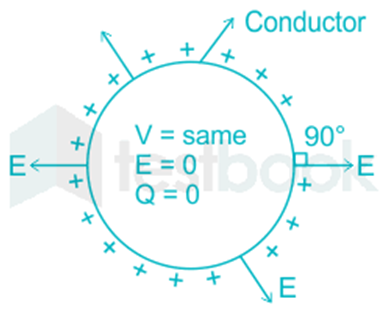
1. Inside the conductor, an electrostatic field is zero.
The conductor has free charges. In the presence of electric fields, these charges experience force and drift. But in the static condition, free charges are distributed in such a way that the Electric field inside the conductor is always zero.
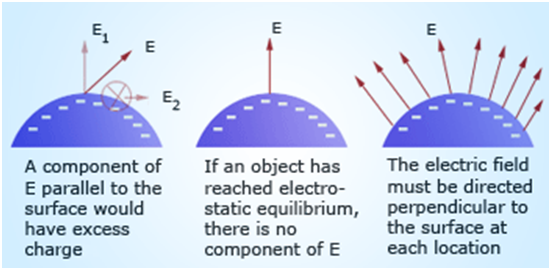
2. At the surface of a charged conductor, the electrostatic field must be normal to the surface at every point.
If the electric field would not normal to the surface, the charges will move due to its tangential component and charges will no longer remain in static condition.
3. The interior of a conductor can have no excess charge in a static situation.
A conductor has an equal number of positive and negative charges inside it in any volume element. Any excess charge must reside on its surface and there is no net charge at any volume of it.

4. The electrostatic potential is constant throughout the volume of the conductor and has the same value (as inside) on its surface.
We have seen that E=0 inside the volume of the conductor, but does it mean that V should also be zero, certainly not!. As the derivative of constant is also zero. The conductor thus has a constant and same value of electrostatic potential inside and on the surface of it. And its value is different outside the conductor.
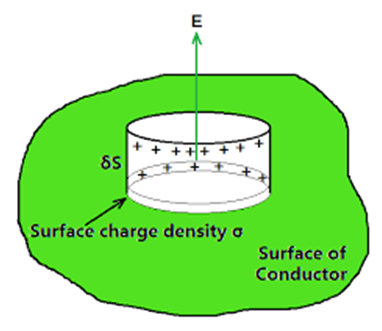
5. Electric field at the surface of a charged conductor
If the conductor has charge density
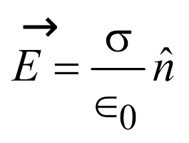
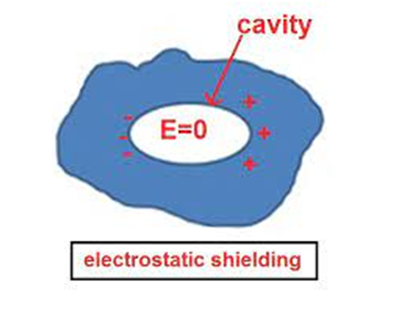
6. Electrostatic shielding.
Consider a cavity of a conductor with no charge inside the cavity. The electric field inside the conductor is zero, whatever be the size or shape of the conductor or whatever be the charge on the conductor on the electric field outside the conductor. This gives rise to a phenomenon called electrostatic shielding. If we place anything inside a conductor it will be shielded from any external field.
Dielectrics and polarization
Dielectrics are non conducting material, which has no charge carriers.
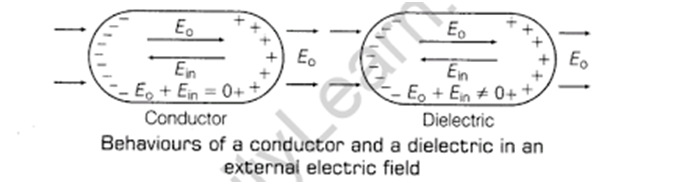
When we put a conductor in an external electric field, the charge inside it moves and arranges in such a way that the electric field induced inside it starts opposing the external field. This will happen till the internal induced field completely cancels the external field and the net field inside the conductor becomes zero.
But in the case of dielectric, in which free movement of charges is not possible when put in an external field, the induced moment is only due to stretching and re-orientation of the molecules of the dielectrics
Here also the induced field will try to oppose the external field but it cannot completely cancel it but can only reduce it.
Enet inside the dielectric = External field Eo - Induced field E.
Types of dielectric materials
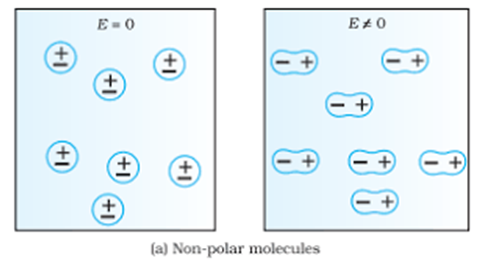
We have two kinds of dielectric materials, one is polar and the other is non-polar

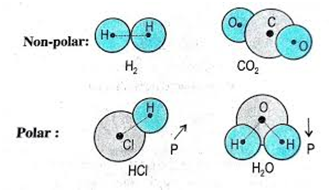
In polar molecules, there is a dipole moment in individual molecules but in the absence of electricity, these molecules are randomly oriented in such a way that the net dipole moment is zero.
But when these molecules are placed in external E, these individual dipoles are aligned in the direction of the Electric field, basically re-orientation of the molecules happens and thus becomes polarized in the presence of the external electric field.
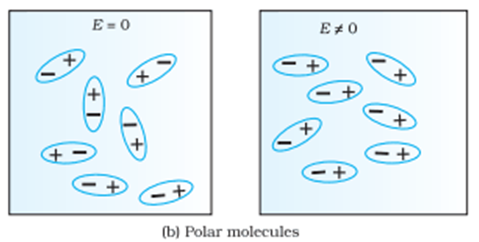
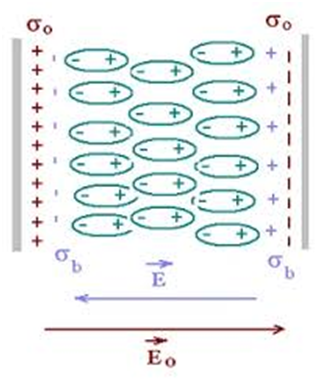
In nonpolar molecules, in the absence of an external electric field, there is no polarization. But when we apply an external electric field the molecule gets stretched and there happens a separation between positive and negative charges. So the polarization of the dipole happens.
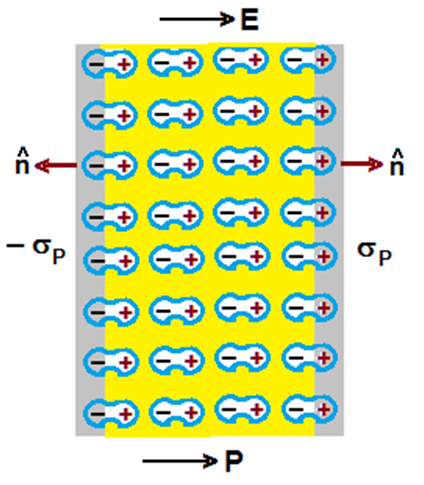
The figure given below it is shown how a dielectric is polarized in presence of an external electric field, note that all the charges shown are actually bound charges and not the free charges. The charges in the bulk of the dielectric neutralize each other and there is a net surface charge on the boundary of the dielectric, the surface gets a surface-bound charge of
2. Potential energy
- Books Name
- Physics Book Part l and ll
- Publication
- Grow Career Publication
- Course
- CBSE Class 12
- Subject
- Physics
Potential energy
Potential energy of a system charge
Electric Potential Energy of a System of Charges Electric potential energy of a system of charges is equal to amount of work done in forming the system of charges by bringing them at their particular positions from infinity without any acceleration and against the electrostatic force. It is denoted by U.
U=W=qV(r)
Potential energy in an external field

consider a system of two charges q1 and q2 located at a distance r1 and r2 from the origin. Let these charges be placed in an external field of magnitude E. Let the work done in bringing the charge q1 from infinity to r1 be given as q1V(r1)and the work done in bringing the charge q2 from infinity to r2 against the external field can be given as q2V(r2).
Potential energy of a dipole in an external field
Consider a dipole with charges q1 = +q and q2 = –q placed in a uniform electric field E, in a uniform electric field, the dipole experiences no net force; but experiences a torque τ given by τ = p×E which will tend to rotate it (unless p is parallel or antiparallel to E).
ELECTROSTATICS OF CONDUCTORS
1. Inside a conductor, electrostatic field is zero
There may also be an external electrostatic field. In the static situation, when there is no current inside or on the surface of the conductor, the electric field is zero everywhere inside the conductor. This fact can be taken as the defining property of a conductor.
2. At the surface of a charged conductor, electrostatic field must be normal to the surface at every point
We can say that, if the electric field lines were not normal at the surface, a component of the electric field would have been present along the surface of a conductor in static conditions. Thus, free charges moving on the surface would also have experienced some force leading to their motion, which does not happen. Since there are no tangential components, the forces have to be normal to the surface.
3. The interior of a conductor can have no excess charge in the static situation
A neutral conductor has equal amounts of positive and negative charges In every small volume or surface element. When the conductor is charged, The excess charge can reside only on the surface in the static situation. This follows from the Gauss’s law.
4. Constant electrostatic potential throughout the volume of the conductor:
The electrostatic potential at any point throughout the volume of the conductor is always constant and the value of the electrostatic potential at the surface is equal to that at any point inside the volume.
5. Electric field at the surface of a charged conductor
Here σ is the surface charge density and nˆ is a unit vector normal to the surface in the outward direction. To derive the result, choose a pill box (a short cylinder) as the Gaussian surface about any point P on the surface. The pill box is partly inside and partly outside the surface of the conductor. It has a small area of cross-section δ S and negligible height.
DIELECTRICS AND POLARISATION
The Dielectric Constant is the ratio of the applied electric field strength to the strength of the decreased value of the electric field capacitor when a dielectric slab is placed between the parallel plates. The formula is as follows:
εr = E0 / E
where E0 is the applied electric field, E is the net field, & εr is the dielectric constant.The greater the dielectric constant, the greater the amount of charge that can be held. The capacitance of a capacitor is increased by a factor of the dielectric constant when the gap between the plates is completely filled with a dielectric. C = εr C0, where C0 is the capacitance between the plates with no dielectric.
3. Capacitors and capacitance
- Books Name
- Physics by Anshu Physics Book
- Publication
- Madhava Publications
- Course
- CBSE Class 12
- Subject
- Physics
Conductor and Capacitors
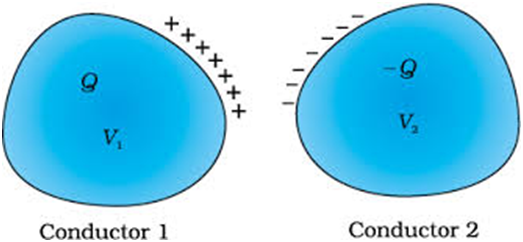
A capacitor is a two-conductor system separated by an insulator. The conductors have charges say Q1 and Q2 and potential V1 and V2. In practice, we have two conductors having charge Q and -Q and the potential difference between them are V= V1-V2.
Note: Even a single conductor can be considered as a capacitor assuming the other at infinity.
Conductors may be charged by connecting them to the terminals of a battery. Q is the charge of one conductor, though the total charge of the capacitor is zero.
- The electric field in the region between the conductors is proportional to the charge Q
Now we also know that V= E*d ………….(2)
where V= potential difference between the conductors.
E= electric field in the region in between the conductors of capacitor
d= distance between two conductors of the capacitors
So we get 1 and 2 equations that
Q
To remove the proportionality, you need to put some proportionality constant.
Q= C *V ………… (3)
where C= proportionality constant is called the capacitance of the capacitor, it basically tells us about the charge holding capacity of a particular capacitor for a given voltage difference across it.
- Capacitance is independent of Q and V
- C is only dependent on the size, shape and separation of the system of conductors
- S.I. unit of capacitance C is Farad. 1 F= 1 C/V
- For large C, V is small for given Q and Q is very large for given V. Hence large charges can be stored by providing a small potential difference.
- For small C, V is large for given Q and Q is small for given V. we would need a large potential difference to get more charges on the capacitor.
Types of capacitors and their capacitances
Capacitors come in different shapes, sizes and separations between the conductors and hence differ in their capacitances.
1. Spherical conductor: It is just a single spherical conductor that can store charge on its surface and is assumed to have another surface at infinity. If the potential of the spherical conductor is V and Q is the charge stored then capacitance can be found as below.

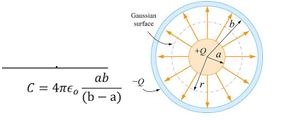
2. Spherical capacitor: It is basically two concentric hollow spheres of inner radius a and outer radii ‘b’. Then capacitance C is given by the following formula.
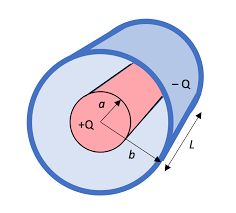
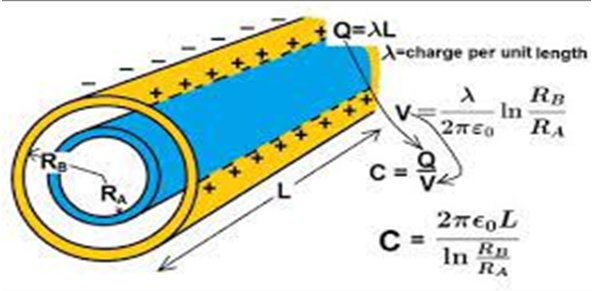
3. Cylindrical capacitor: It is made of two concentric cylindrical conductors, having length ‘l; and inner and outer radius as ‘a’ and ‘b’ respectively.
4. Parallel Plate capacitor
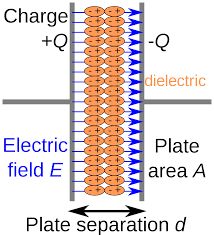
In a parallel plate capacitor, we have two parallel plates of surface area ‘A’ and the distance between plates is ‘d’. The capacitance of parallel is given by the following formula.
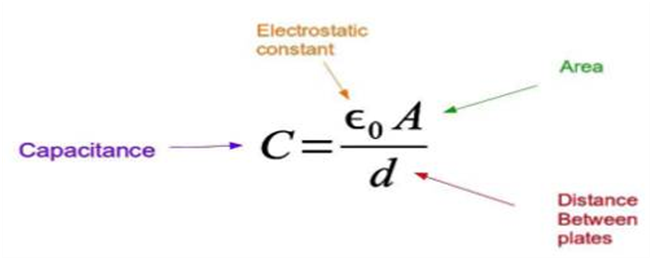
This is how we can find the capacitance of the parallel plate capacitor.
Below are some equations used in the case of parallel plate capacitors.

Effect of dielectric on capacitance
Suppose we don't have air or vacuum between the conductors of the capacitor but the space between them is filled by an insulator or a dielectric of dielectric constant ‘ K’ or relative permittivity ‘
Suppose we have a parallel plate capacitor filled with dielectric in all space between the plates. Then the new capacitance becomes K time the previous value of capacitance with air/vacuum between the plates.
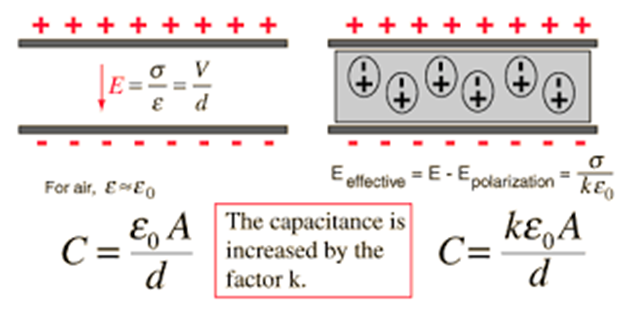
This is true not only for parallel plate capacitors but valid with every kind of capacitor spherical and cylindrical too. When we filled the space between the conductor their capacitance becomes K or
When we fill dielectric of thickness ‘t’ in between the plates of parallel plate capacitors such that t<d.
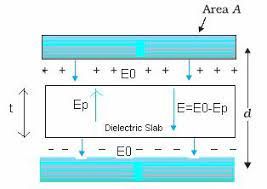
It means the space between the plates is filled with air in thickness (d-t) and filled with dielectric in thickness ‘t’.

Above the formula, we use to find the capacitance if a dielectric of thickness t< d is introduced between the plates in a parallel plate capacitor.
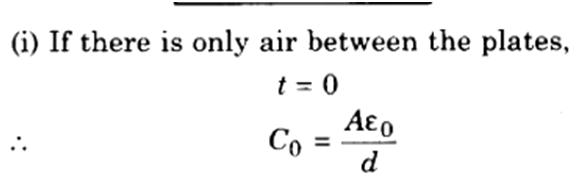
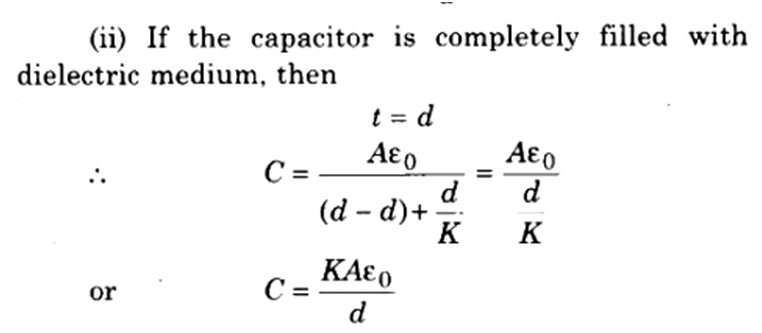
Some definitions :
Dielectric constant
We know that when we insert dielectric inside the capacitor, capacitance becomes C= K* Co
So K= C/Co
The dielectric constant may be defined as the ratio of the capacitance of the capacitor when it is filled with a dielectric to the capacitance when air/ vacuum is in between.
Combination of capacitors
We can combine several capacitors and capacitance C1, C2… Cn to obtain a system with some effective capacitance C. The effective capacitance depends on the way individual capacitors are combined.
The two simplest ways are
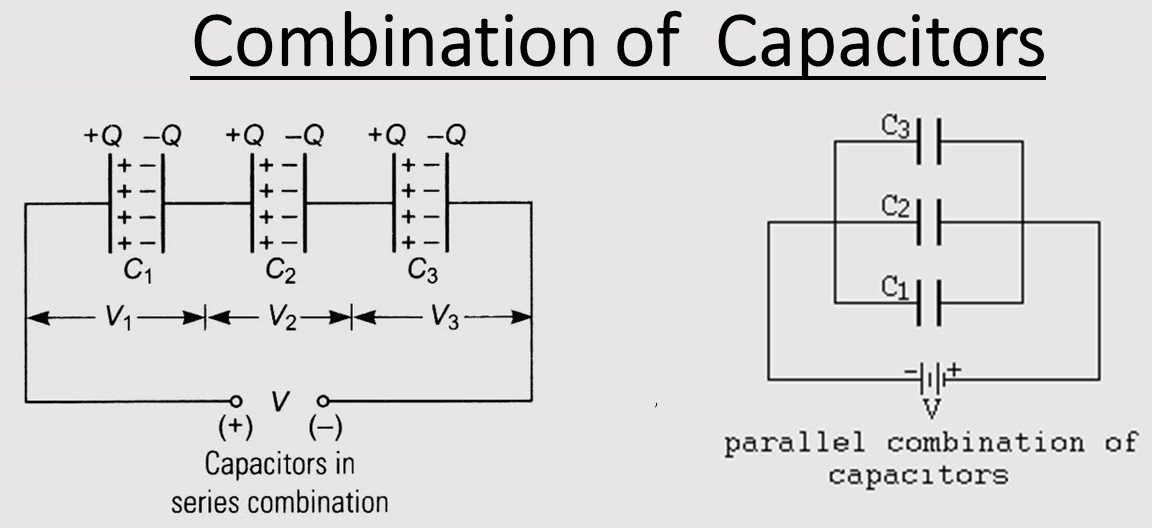
- Capacitors in series .
- Capacitors in parallel.
Capacitors in series
When the second plate of one capacitor is directly connected with the first plate of another capacitor, this is called a series combination of the capacitors.
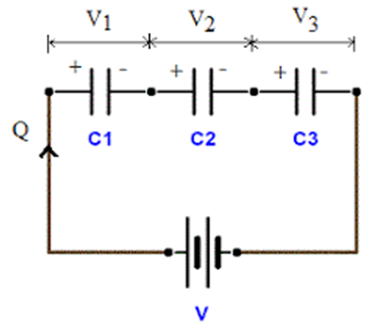
In series, the combination of the capacitor charge is the same for all the capacitors and the voltage of the battery is the sum of the voltage drop of the individual capacitor.
V= V1 + V2+ V3 ; Q1= Q2= Q3= Q
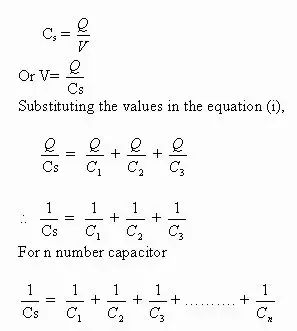
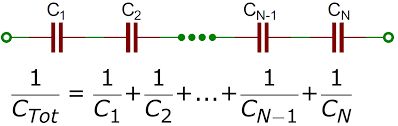
We can conclude that the effective capacitance of a capacitor in series is the ‘n’ number of capacitors connected in series.
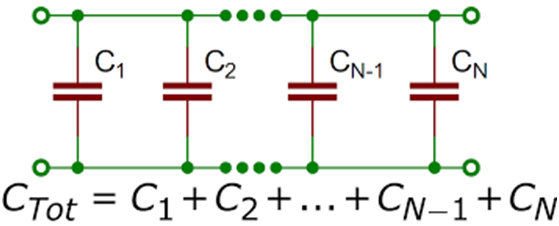
Capacitor in parallel
In the figure given below, capacitors are connected in parallel combinations. In parallel combination we have the following:
- The voltage difference is the same across every capacity
V1= V2= V3= V
- A charge is different across each capacitor and the total charge in the circuit is actually the sum of the charge on the individual capacitor
Q= Q1+ Q2+ Q3
Q= Q1 + Q2+ Q3
Ceq*V= C1*V+ C2*V+ C3*V
Ceq= C1 + C2 + C3

If we have ‘n’ capacitors in parallel then the effective capacitance of the parallel combination of capacitors is given by following
Energy stored in a capacitor
In the process of charging the capacitor, some energy is stored in the capacitor. If you are wondering where this energy comes from. Imagine the process of charging the capacitor.
In the circuit given below, the positive terminal of the battery is connected with the upper plate and the negative terminal is connected with the lower plate. So the upper plate is at a higher potential than the lower.
Initially, we assume that both the plates are uncharged and then after connecting it with the battery, there starts a transfer of charge from the lower conductor to the upper conductor bit by bit, so at the end, the upper plate gets ‘Q’ charge while the lower plate gets ‘-Q’ charge when fully charged.
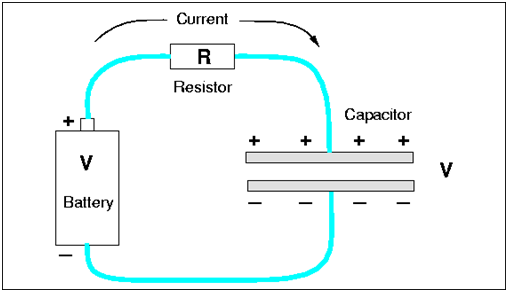
Since the charge is being transferred from lower potential to higher potential, work will be done externally and this external work is stored in the form of energy in the capacitor. The various formula for energy stored in the capacitor in terms of charge, capacitance and the potential difference between the plates is given below

The energy density in a parallel plate capacitor = Energy/volume

A fun thing to do.
Below is the link to the simulation of the capacitor. In this simulation, we have a battery connected with a parallel plate capacitor.
What you have to do -
- The potential of the battery can be changed by moving the slider up and down given on the battery.
- You can increase the plate area by dragging the arrow diagonally as shown in the simulator screen
- And you can also increase or decrease the distance between the plates by dragging the arrow up and down
- Take out the potentiometer by dragging it and connect it with two plates of the capacitor and measure the potential difference on the plates
What you can get from here.
For a given combination of battery potential, separation of plates and plate area you can see the value of the following quantities by clicking on the checkbox before it.
- Capacitance
- Charge on plates
- Energy stored in the capacitor
Also, you can see the visually
- Charges on the plated
- Electric field
- Current direction
- And bar graphs
3. Capacitors and capacitance
- Books Name
- Physics Book Part l and ll
- Publication
- Grow Career Publication
- Course
- CBSE Class 12
- Subject
- Physics
Capacitors and capacitance
CAPACITORS AND CAPACITANCE
A capacitor is a two-terminal electrical device that possesses the ability to store energy in the form of an electric charge. It consists of two electrical conductors that are separated by a distance. The space between the conductors may be filled by vacuum or with an insulating material known as a dielectric. The ability of the capacitor to store charges is known as capacitance. C =Q/v
THE PARALLEL PLATE CAPACITOR
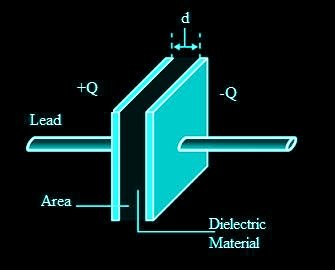
A parallel plate capacitor consists of two large plane parallel conducting plates separated by a small distance We first take the intervening medium between the plates to be vacuum. The effect of a dielectric medium between the plates is discussed in the next section.
![]()
COMBINATION OF CAPACITORS
Capacitance in Series
Figure 1a shows a series connection of three capacitors with a voltage applied. As for any capacitor, the capacitance of the combination is related to charge and voltage by C= Q/V
Note in Figure 1 that opposite charges of magnitude Q flow to either side of the originally uncharged combination of capacitors when the voltage V is applied. Conservation of charge requires that equal-magnitude charges be created on the plates of the individual capacitors, since charge is only being separated in these originally neutral devices. The end result is that the combination resembles a single capacitor with an effective plate separation greater than that of the individual capacitors alone. Larger plate separation means smaller capacitance. It is a general feature of series connections of capacitors that the total capacitance is less than any of the individual capacitances.
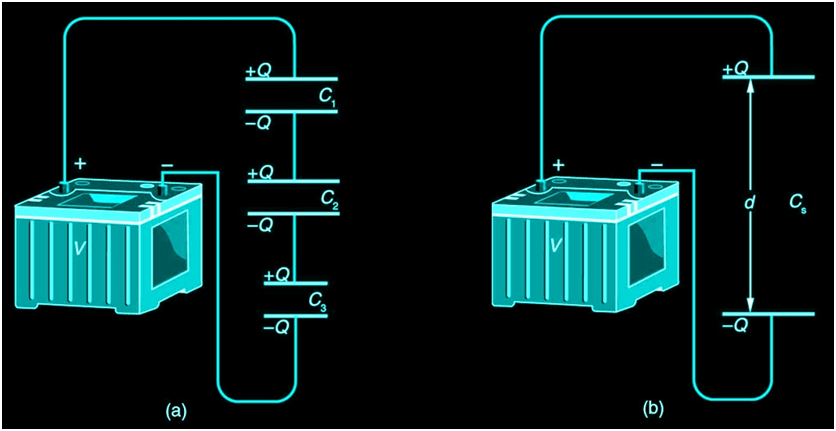
dividual capacitors Solving C=Q/V for V gives V=Q/C. The voltages across the individual capacitors are thus
V1=Q/C1,V2=Q/C2, and V3=Q/C3.
The total voltage is the sum of the individual voltages:
V = V1 + V2 +V3.
Now, calling the total capacitance CS for series capacitance, consider that
V=Q/Cs =V1+V2+V3.
Entering the expressions for V1, V2, and V3, we get
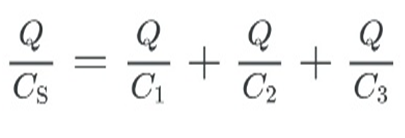
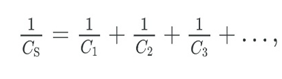
where “…” indicates that the expression is valid for any number of capacitors connected in series. An expression of this form always results in a total capacitance CS that is less than any of the individual capacitances C1, C2, …, as Example 1 illustrates.
Total Capacitance in Series, Cs
Total capacitance in series:
1/CS = 1/C1 + 1/C2 … ..
Capacitors in parallel
Two capacitors arranged in parallel. In this case, the same potential difference is applied across both the capacitors. But the plate charges (±Q1) on capacitor 1 and the plate charges (±Q2) on the capacitor 2 are not necessarily the same:
Q1 = C1V, Q2 = C2V
The equivalent capacitor is one with charge
Q = Q1 + Q2
and potential difference V.
Q = CV = C1V + C2V
The effective capacitance C is, C = C1 + C2
VAN DE GRAAFF GENERATOR
A Van de Graaff generator is an electrostatic generator, invented by Robert J. Van de Graaff. It uses a moving belt that accumulates charge on a hollow metal structure designed like a globe, placed on the top of a column that is insulating in nature and thus, creating a very high electric potential in the order of a few million volts. This results in a very large electric field that is used to accelerate charged particles.
Working principle of Van de Graaff Generator
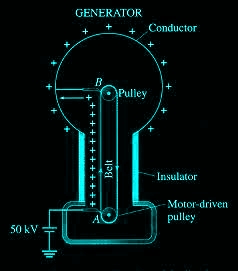
Let us consider a large spherical shell of radius R. If we place a charge of magnitude Q on such a sphere, the charge will spread uniformly over the surface of the sphere and the electric field inside the sphere will be equal to zero, and that outside the sphere will be due to the charge Q placed at the centre of the sphere.
At the surface of the small sphere:
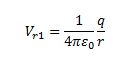
At the large spherical shell of radius R:
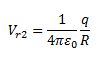
If we consider the total charges in the system, that is, q and Q, then the total potential energy due to the system of charges can be given as,
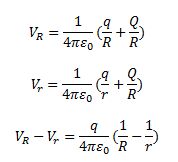

 Madhava Publications
Madhava Publications
 Grow Career Publication
Grow Career Publication