Chapter 4 Work, energy and power

Introduction

→ The energy for the ‘life processes’ comes from food. Activities like playing, singing, reading, w

thinking, jumping, cycling and running requires energy.

Work

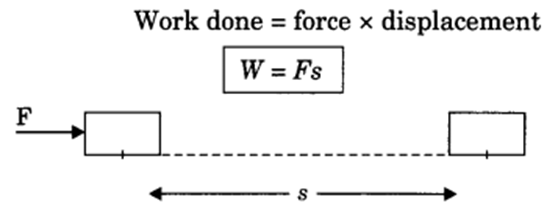
Work done on an object is defined as the product of the magnitude of the force acting on the body and the displacement in the direction of the force.

W = F.s

If a force acting on a body causes no displacement, the work done is 0. For example, pushing a wall.

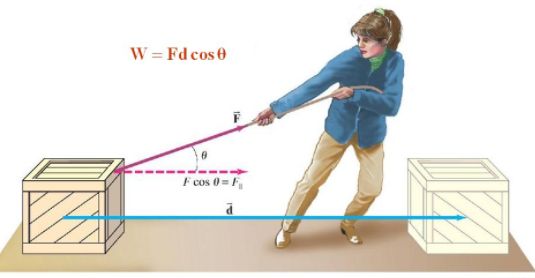
Two conditions need to be satisfied for work to be done:
(i) A force should act on object
(a) The object must be displaced
Work = Force x Displacement

Unit of workdone = Joule = Newton x metre

1 Joule work is said to be done when 1 Newton force is applied on an object and it shows the displacement by 1 meter.
 

Energy

Energy is defined as the ability to do work. Its unit is the same as that of work.

SI unit of energy or work = Joule (Nm)

Energy has different forms: Light, heat, chemical, electrical or mechanical.

Mechanical energy is the sum of:
(i) Kinetic energy (K.E)
(ii) Potential energy (P.E)

Power

The rate of doing work or the rate of transfer of energy is called power. It is denoted by P

⇒ P = Wt

SI unit is Watt (J/s).

Average power = Total energy consumed / Total time taken

The commercial unit of power is kWh i.e. energy used in 1 hour at 1000 Joules/second.
1KWh = 3.6×10⁶ J

Kinetic Energy

Objects in motion possess energy and can do work. This energy is called Kinetic Energy.
F = ma.
Also W = F.s
⇒ From the 2nd equation of motion v²−u²=2as,
⇒ we get s = v²−u² / 2a

Substituting equation for work done by a moving body,
⇒ we get W =m.a * v²−u² / 2a

Or

⇒ Kinetic Energy = K.E= 1/2 mv² (taking initial velocity u=0)

When two identical bodies are in motion, the body with a higher velocity has more K.E.

Work-energy theorem

The work-energy theorem states that the net work done by a moving body can be calculated by finding the change in KE.

⇒ W_net = KE_final− KE_initial

⇒ W_net = 1/2 mv²

Factors affecting kinetic energy

• Mass
• Velocity
• Momentum

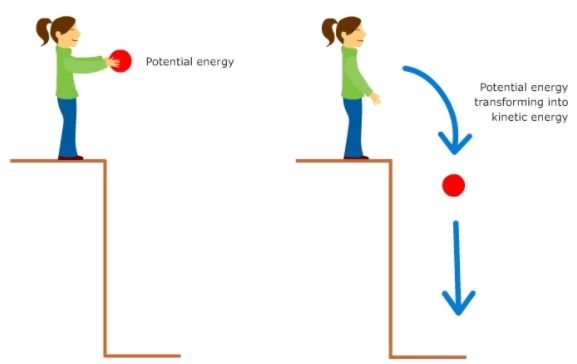
Potential Energy

Energy can get stored in an object when work is done on it.

For example, stretching a rubber string. The energy that is possessed by a body by virtue of its configuration or change in position is known as Potential Energy.

The potential energy of an object at a height.
When an object is raised to a certain height, work is done against gravity to change its position. This energy is stored as Potential Energy.

⇒W = F.s

⇒F = ma
In the case of increasing the height, F = mg
Therefore, W (P.E) = mgh
⇒ ΔPE = mg(h_final - h_{initial )}

Law of Conservation of Energy

Law of conservation of energy states that energy can neither be created nor destroyed, but can be transferred from one form to another. The total energy before and after the transformation remains constant.

For example: consider a ball falling freely from a height.

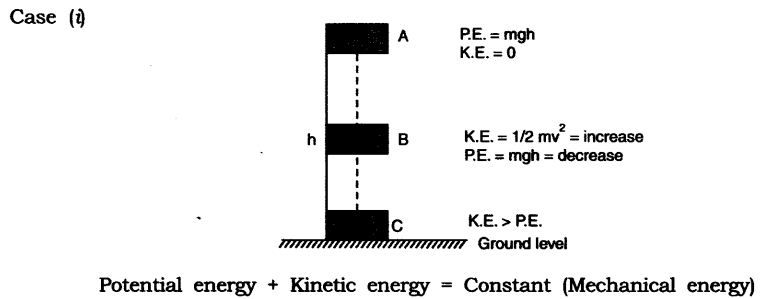
Potential energy + Kinetic energy = Constant (Mechanical energy)
A body of mass ‘m’ is raised to height ‘h’ at A its potential energy is maximum and kinetic energy is 0 as it is stationary.
When body falls at B, h is decreasing hence potential energy decreases and V is increasing hence kinetic energy is increasing.
When the body is about to reach the ground level, h = 0, v will be maximum hence kinetic energy –> potential energy
Decrease in potential energy = Increase in kinetic energy
This shows the continual transformation of gravitational potential energy into kinetic energy.

Introduction

→ The energy for the ‘life processes’ comes from food. Activities like playing, singing, reading, w

thinking, jumping, cycling and running requires energy.

Work and Energy

Introduction

Work done

Work done on an object is defined as the product of the magnitude of the force acting on the body and the displacement in the direction of the force. W = F.s
If a force acting on a body causes no displacement, the work done is 0. For example, pushing a wall.
Two conditions need to be satisfied for work to be done:

(i) A force should act on object
(ii) The object must be displaced

•    W = Fs
If F = 1 N and s = 1 m
W= 1 N x 1 Nm
W = 1 Nm
1j =1 Nm

•     1 J is the amount of work done on an object when a force of 1 N displaces it by 1 m along the line of action of the force.

•    Work done has only magnitude and no direction i.e., work is a scalar quantity.
•    SI unit of work is joule (J).
•    1 joule (one joule)
 

Work

Work done on an object is defined as the product of the magnitude of the force acting on the body and the displacement in the direction of the force.

W = F.s

If a force acting on a body causes no displacement, the work done is 0. For example, pushing a wall.

Two conditions need to be satisfied for work to be done:
(i) A force should act on object
(a) The object must be displaced
Work = Force x Displacement

Unit of workdone = Joule = Newton x metre

1 Joule work is said to be done when 1 Newton force is applied on an object and it shows the displacement by 1 meter.
 

Types of work

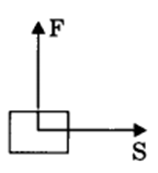
(i) Zero work: If the angle between force and displacement is 90°, then work done is said to be zero work.
Example: When a man carries a load on his hand and moves on a level road, work done by the man on the load is zero.

(ii) Positive work: Work done is said to be positive if force applied on an object and displacement are in the same direction.

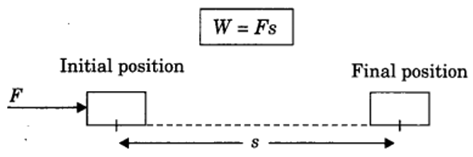
Example: Work done by the force of gravity on a falling body is positive.

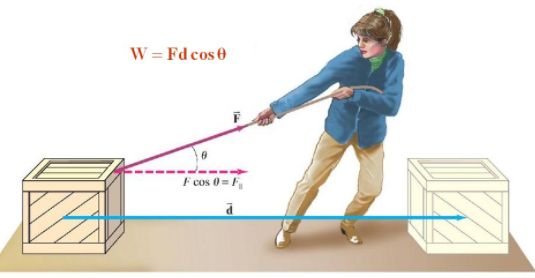
(iii) Negative work: Work done is said to be negative if the applied force on an object and displacement are in opposite direction.
W = -Fs
Here displacement is taken to be negative (-s).

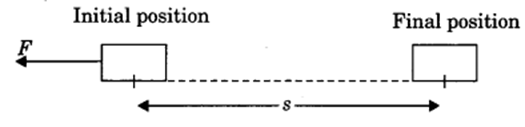
Example: Work done by friction force is usually negative on a moving body.

Energy

Energy is defined as the ability to do work. Its unit is the same as that of work.

SI unit of energy or work = Joule (Nm)

Energy has different forms: Light, heat, chemical, electrical or mechanical.

Mechanical energy is the sum of:
(i) Kinetic energy (K.E)
(ii) Potential energy (P.E)

Kinetic Energy

Objects in motion possess energy and can do work. This energy is called Kinetic Energy.
F = ma.
Also W = F.s
⇒ From the 2nd equation of motion v²−u²=2as,
⇒ we get s = v²−u² / 2a

Substituting equation for work done by a moving body,
⇒ we get W =m.a * v²−u² / 2a

Or

⇒ Kinetic Energy = K.E= 1/2 mv² (taking initial velocity u=0)

When two identical bodies are in motion, the body with a higher velocity has more K.E.

Work-energy theorem

The work-energy theorem states that the net work done by a moving body can be calculated by finding the change in KE.

⇒ W_net = KE_final− KE_initial

⇒ W_net = 1/2 mv²

                                                Energy

Energy of a body is defined as the capacity or ability of a body to do work.
The SI unit of energy is joule (J)
Forms of energy

There are various forms of energy in the nature, few of them are mechanical energy (potential energy + kinetic energy) heat energy, chemical energy and light energy.

1. Mechanical energy
Mechanical energy includes kinetic energy and potential energy.

a)  Kinetic energy
The energy possessed by a body by the virtue of its motion is called kinetic energy.
Kinetic energy possessed by a body can be calculated by
EK=1/2 mv2
m = mass of body
V = velocity of body

Derivation of kinetic energy

Let us consider an object lying on a frictionless surface having mass ‘m’

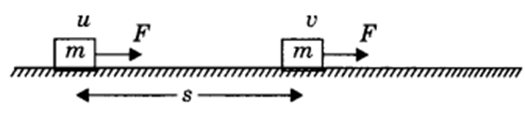
A force of constant magnitude F is acting on the body. Here initial velocity of the body is u and final velocity is v. As there is no dissipative forces, work done on the body will be stored in the form of change in kinetic energy.
W=Fs

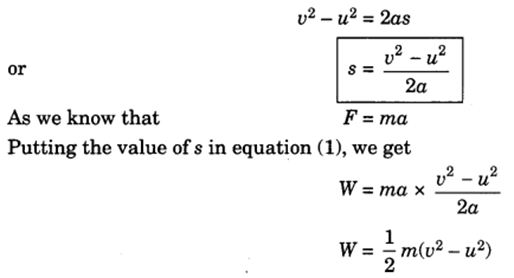
If the object is starting from a stationary position u = 0, then

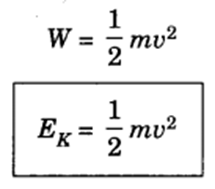
Factors affecting Kinetic energy

•    Mass
•    Velocity
•    Momentum
b) Potential energy

The energy possessed by a body due to its position or configuration is called potential energy.

(i) Gravitational potential energy

Potential energy at any height (h) from a reference can be calculated by formula
Ep = mgh
where, m = mass of object
v = height from reference
The gravitational potential energy of an object at a point above the ground is defined as the work done in raising it from the ground to that point against gravity.

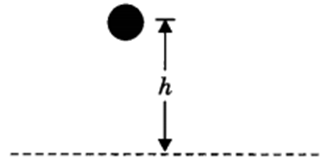
Derivation of potential energy
When work is done on the body, the work is stored in the form of energy. Consider an object of mass, m. Let it be raised through a height, h from the ground. A force is required to do this. The minimum force required to raise the object is equal to the weight of the object, mg. The object gains energy equal to the work done on it. Let the work done on the object against gravity be W.

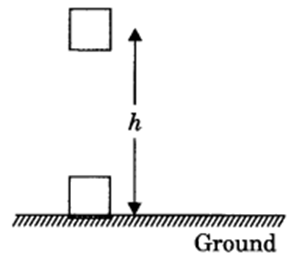
W = force x displacement
= mgh.
Since work done on the object is equal to mgh, an energy equal to mgh units is gained by the object. This is the potential energy (Ep) of the object.
Ep = mgh
 

Work-energy theorem

The work-energy theorem states that the net work done by a moving body can be calculated by finding the change in KE.

⇒ W_net = KE_final− KE_initial

⇒ W_net = 1/2 mv²

Factors affecting kinetic energy

• Mass
• Velocity
• Momentum

Potential Energy

Energy can get stored in an object when work is done on it.

For example, stretching a rubber string. The energy that is possessed by a body by virtue of its configuration or change in position is known as Potential Energy.

The potential energy of an object at a height.
When an object is raised to a certain height, work is done against gravity to change its position. This energy is stored as Potential Energy.

⇒W = F.s

⇒F = ma
In the case of increasing the height, F = mg
Therefore, W (P.E) = mgh
⇒ ΔPE = mg(h_final - h_{initial )}

Law of Conservation of Energy

Law of conservation of energy states that energy can neither be created nor destroyed, but can be transferred from one form to another. The total energy before and after the transformation remains constant.

For example: consider a ball falling freely from a height.

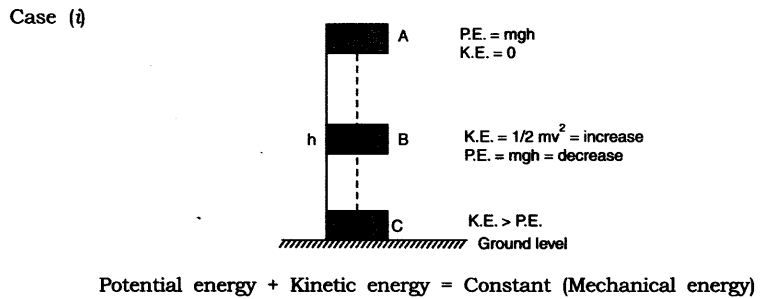
Potential energy + Kinetic energy = Constant (Mechanical energy)
A body of mass ‘m’ is raised to height ‘h’ at A its potential energy is maximum and kinetic energy is 0 as it is stationary.
When body falls at B, h is decreasing hence potential energy decreases and V is increasing hence kinetic energy is increasing.
When the body is about to reach the ground level, h = 0, v will be maximum hence kinetic energy –> potential energy
Decrease in potential energy = Increase in kinetic energy
This shows the continual transformation of gravitational potential energy into kinetic energy.

Power

The rate of doing work or the rate of transfer of energy is called power. It is denoted by P

⇒ P = Wt

SI unit is Watt (J/s).

Average power = Total energy consumed / Total time taken

The commercial unit of power is kWh i.e. energy used in 1 hour at 1000 Joules/second.
1KWh = 3.6×10⁶ J

                           Law of Conservation of Energy

Energy can neither be created nor destroyed, it can only be transformed from one form to another. The total energy before and after transformation remains the same.

Total energy = KE + PE

For example: consider a ball falling freely from a height. At height h, it has only PE = mgh.
By the time it is about to hit the ground, it has a velocity and therefore has KE=  
 mv2. Therefore, energy gets transferred from PE to KE, while the total energy remains the same.

Power (P)
Power is defined as the rate of doing work or rate of transfer of energy.
Power = work/time
P=W/T

•    Unit of power is watt (W).
Watt


 

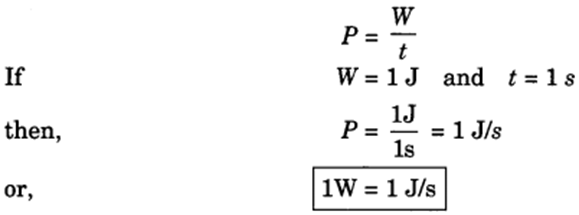
Commercial unit of energy

•    Kilowatt hour (kWh) or 1 unit
•    The energy used in households, industries and commercial establishments are usually expressed in kilowatt hour.
•    1 kWh is the energy used in one hour (1 h) at the rate of 1000 J/s or (1 kW).
∴1 kWh =l kW x U = 1000 W x 3600 s = 3600000 J
1 kWh = 3.6 x 106 J = 1 unit
 

 Power can also be represented as,
P = Fv
F = force applied
v = velocity of object
P=W/t=Fs/t=Fv