Distance and displacement, velocity;
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Distance and Displacement
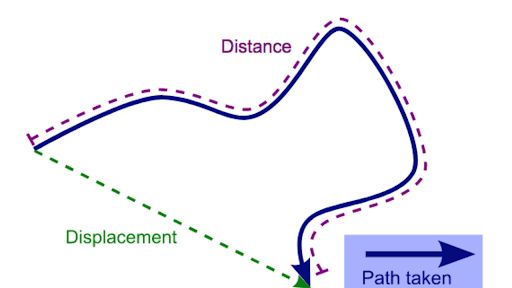
Distance -The actual path or length travelled by the object travelled by the object is called the distance.
It is a scalar quantity.
It is always positive.
It can never be zero or negative.
Displacement – It is the shortest path between initial and final point.
It is a vector quantity.
It can be positive or negative.
It can be zero.
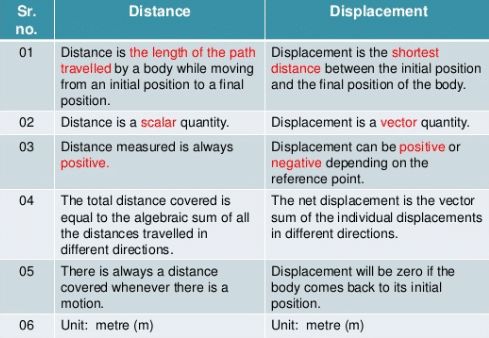
Difference bw distance and displacement
Example 1: A body travels in a semicircular path of radius 10 m starting its motion from point ‘A’ to point ‘B’. Calculate the distance and displacement.
Example 2: A body travels 4 km towards North then he turn to his right and travels another 4 km before coming to rest. Calculate (i) total distance travelled, (ii) total displacement.
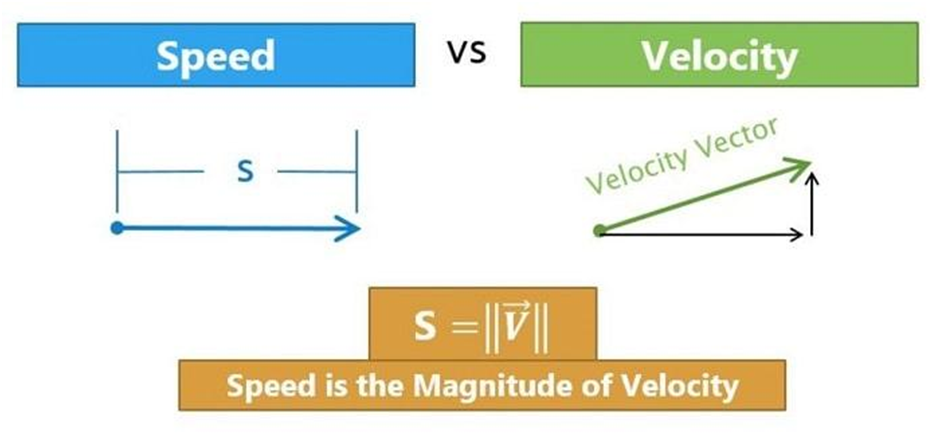
Velocity - It is defined as the displacement of the body per unit time.
Velocity = displacement travelled / time taken
SI unit = m/s (meter/second)
Average Velocity - The average velocity of a body is the total displacement travelled by the total time taken to cover this distance.
Average velocity= Total Displacement/Total Time taken
Avg. Velocity (vavg) = (Initial velocity + Final velocity)/2 = (u+v)/2
where, u = initial velocity, v = final velocity
Example 1: During first half of a journey by a body it travel with a speed of 40 km/hr and in the next half it travels with a speed of 20 km/hr. Calculate the average speed of the whole journey.
Example 2 : If Ananya was able to travel 6 km in North in 2 hour in his car. What was her velocity?
Example 3: A car travels 20 km in first hour, 40 km in second hour and 30 km in third hour. Calculate the average speed of the train.
uniform and non-uniform motion along a straight line
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Uniform Motion and Non-uniform Motion
Uniform motion - When a body covers equal distances in equal intervals of time then the body is said to describe uniform motion.
Non uniform motion - When a body moves unequal distances in equal intervals of time or vice-versa, then the body is said to describe non-uniform motion.

acceleration
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Acceleration -
Acceleration is seen in non-uniform motion and it can be defined as the rate of change of velocity with time.
Acceleration (a) = Change in velocity/Time = (v-u)/t
where, v = final velocity, u = initial velocity
If v > u, then ‘a’ will be positive (+ve).
Retardation/Deceleration -
Deceleration is seen in non-uniform motion during decrease in velocity with time. It has same definition as acceleration
Deceleration (a') = Change in velocity/Time = (v-u)/t
Here, v < u, ‘a’ = negative (-ve).
It is a vector quantity.
SI unit – m/s2 ( meter per second square)
Example 1: A car speed increases from 40 km/hr to 60 km/hr in 5 sec. Calculate the acceleration of car.
Example 2: A car travelling with a speed of 20 km/hr comes into rest in 0.5 hrs. What will be the valu of its retardation?
EXAMPLE 3 : If the velocity of the car reduced to 80 m/s from 120 m/s in 8 seconds on applying breaks . Calculate its acceleration
distance-time and velocity-time graphs for uniform motion and uniformly accelerated motion
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Uniform Acceleration - If the change in velocity in equal intervals of time is always the same, then the object is said to be moving with uniform acceleration.
Example: a body falling from a height towards the surface of the earth.
Non-uniform or Variable Acceleration- If the change in velocity in equal intervals of time is not the same, then the object is said to be moving with variable acceleration.
Example - A ball thrown vertically upwards is moving with a negative acceleration as the velocity decreases with time.
Graphs for Motion -
1) Distance-time graphs (s-t graphs)
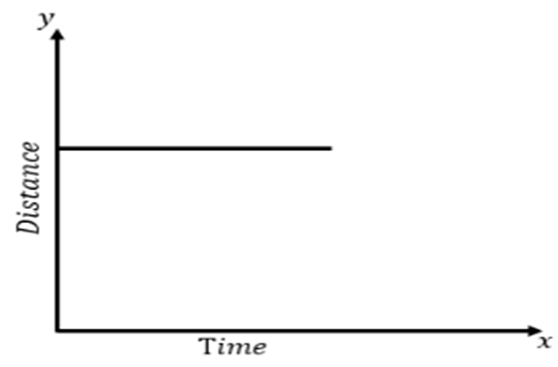
a) When the object is stationary or at rest -
The distance time graph for stationary object is the line parallel to time axis.
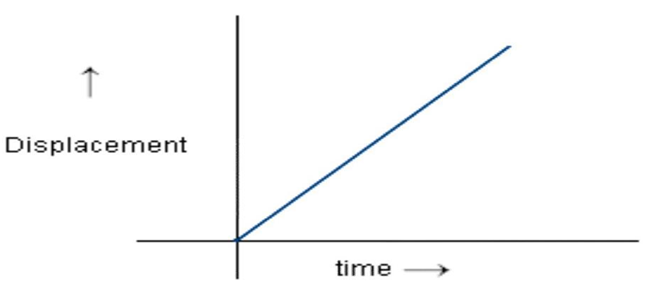
b) When object is in uniform motion -
The distance time graph for the object moving in uniform motion is the straight line inclined to time axis
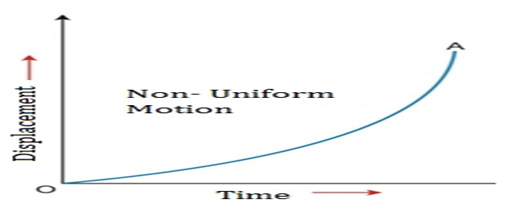
C) When object is in non-uniform motion -
The distance time graph for object moving in non -uniform motion is the curved line.
Important results of distance time graphs -
1) area under curve of s-t graph = displacement/distance travelled by the object
2) slope of s-t graph = velocity of the object
equations of motion by graphical method
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Definition of Equations of Motion
Equations of motion, in physics, are defined as equations that describe the behaviour of a physical system in terms of its motion as a function of time.
There are three equations of motion that can be used to derive components such as displacement(s), velocity (initial and final), time(t) and acceleration(a). The following are the three equation of motion:
First Equation of Motion : v=u+at
Second Equation of Motion : s=ut+1/2 at2
Third Equation of Motion : v2=u2+2as
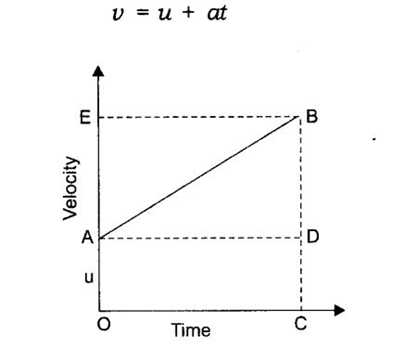
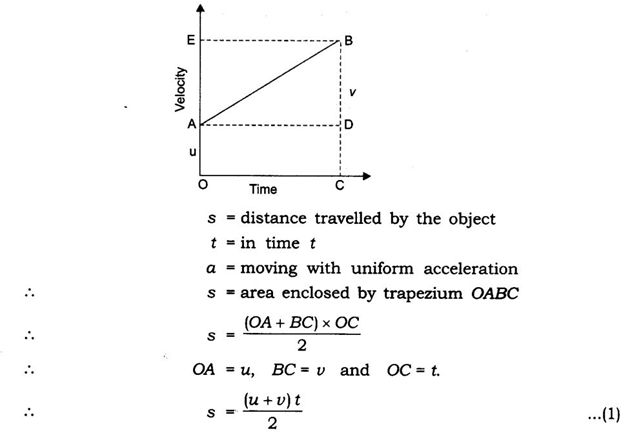
DERIVATION OF FIRST EQUATION OF MOTION ( V = u+at )
Consider a body of mass “m” having initial velocity “u”. Let after time “t” its final velocity becomes “v” due to uniform acceleration “a”.
Now as we know that,
Acceleration = change in velocity/Time taken Acceleration = Final velocity-Initial velocity / time taken
a = v-u/t
=> at = v-u
or v = u + at
This is the first equation of motion.
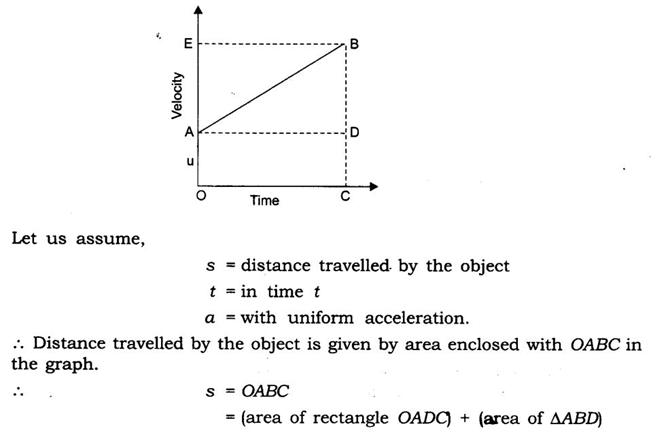
DERIVATION OF SECOND EQUATION OF MOTION (S=ut+1/2 at2 )
Consider a body of mass “m” having initial velocity “u”. Let after time “t” its final velocity becomes “v” due to uniform acceleration “a”. Let the distance travelled by the body be “s”.
Now As we know that,
Distance = Average velocity X Time
Also, Average velocity = u+v/2
Distance (s) = ( u+v ) *t/2 …….eq.(1)
Again we know that, v = u + at
By substituting this value of “v” in eq.(1), we get
Distance(s) = (u+u+at) *t/2
=> s = (2u+at)* t/2
=> s = 2ut/2+at2/2
=>s = ut+ at2/2
or s = ut + 1/2 at2
This is the second equation of motion.
DERIVATION OF THIRD EQUATION OF MOTION (V2 = u2+2as)
Consider a body of mass “m” having initial velocity “u”. Let after time “t” its final velocity becomes “v” due to uniform acceleration “a”. Let the distance travelled by body be “s”.
Displacement=(Initial Velocity+Final Velocity)×t/2
Substituting the standard notations, the above equation becomes
s=(u+v)×t/2
From the first equation of motion, we know that
v=u+at
Rearranging the above formula, we get
t=v−u/a
Substituting the value of ‘t’ in the displacement formula, we get
s=(v+u)/2 *(v−u)/a
s=(v2 - u2)/2a
2as= v2 - u2
Rearranging, we get
v2 – u2= 2as
This is the third equation of motion.
elementary idea of uniform circular motion.
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Introduction To Uniform Circular Motion
We have come across different types of motions in our previous sessions. Rotatory motion, rectilinear motion, oscillatory motion, uniform circular, and periodic motion are some types of motion. Movement of an object while rotating along a circular path is known as circular motion. Circular motion can be either uniform or non-uniform. In this article, let us discuss in brief the uniform circular motion along with examples.
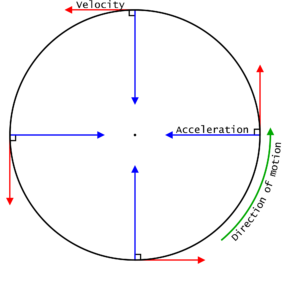
What is Uniform Circular Motion?
The movement of a body following a circular path is called a circular motion. Now, the motion of a body moving with constant speed along a circular path is called Uniform Circular Motion. Here, the speed is constant but the velocity changes.
NOTE -
So if a particle is moving in a uniform circular motion:
Its speed is constant
Velocity is changing at every instant
Uniform Circular Motion Examples
Following are the examples of uniform circular motion:
Motion of artificial satellites around the earth is an example of uniform circular motion. The gravitational force from the earth makes the satellites stay in the circular orbit around the earth.
The motion of electrons around its nucleus.
The motion of blades of the windmills.
The tip of second’s hand of a watch with circular dial shows uniform circular motion.
Formula for velocity in UCM -
V=2πR/T
where R is radius of circle, T is time taken
FRAME OF REFERENCE
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Rest & Motion Relative terms?
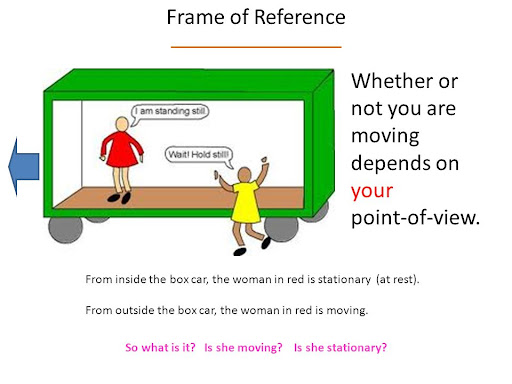
Frame of Reference - A frame of reference is another object or scene with respect to which we compare an object's position.
Objects changing positions with time with respect to the frame of reference are in motion while those which do not change position are at rest.
For example – A passenger sitting on a moving bus is at rest with respect to his co-passenger but at the same time, he is moving with the bus with respect to a person standing outside.
INTRODUCTION
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Introduction –
• In the physical world, one of the most common phenomena is motion.
• The branch of Physics, which deals with the behavior of moving objects, is known as mechanics.
• Mechanics is further divided into two sections namely Kinematics and Dynamics.
• Kinematics deals with the study of motion without taking into account the cause of motion.
• Dynamics is concerned with the cause of motion, namely force.
Motion and Rest -
• An object is said to be in motion if it changes its position with respect to its surroundings in a given time.
• An object is said to be at rest if it does not change its position with respect to its surroundings.
distance and displacement
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Distance and Displacement
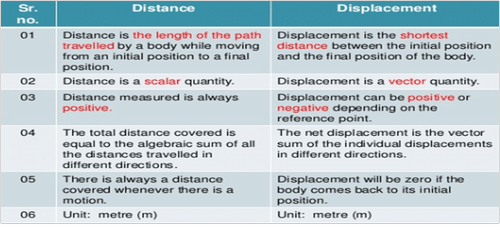
Distance -The actual path or length travelled by the object travelled by the object is called the distance.
- It is a scalar quantity.
- It is always positive.
- It can never be zero or negative.
Displacement – It is the shortest path between initial and final point.
- It is a vector quantity.
- It can be positive or negative.
- It can be zero.
Difference b\w distance and displacement
• Example 1: A body travels in a semicircular path of radius 10 m starting its motion from point ‘A’ to point ‘B’. Calculate the distance and displacement.
• Example 2: A body travels 4 km towards North then he turn to his right and travels another 4 km before coming to rest. Calculate (i) total distance travelled, (ii) total displacement.
Speed
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Speed -
The measurement of distance travelled by a body per unit time is called speed.
Speed (v) = Distance Travelled/Time Taken = s/t
SI unit = m/s (meter/second)
Average Speed - The average speed of a body is the total distance travelled by the total time taken to cover this distance.
Average speed= Total Distance travelled / Total Time taken
EXAMPLE 1 - You walk 60 m at a speed of 3m/s and then run 140m at a speed of 7m/s along a straight track. Find the average speed?
EXAMPLE 2 - What will be the speed of body in m/s and km/hr if it travels 40 kms in 5 hrs ?
1. Introduction
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Introduction –
• In the physical world, one of the most common phenomena is motion.
• The branch of Physics, which deals with the behavior of moving objects, is known as mechanics.
• Mechanics is further divided into two sections namely Kinematics and Dynamics.
• Kinematics deals with the study of motion without taking into account the cause of motion.
• Dynamics is concerned with the cause of motion, namely force.
Motion and Rest
• An object is said to be in motion if it changes its position with respect to its surroundings in a given time.
• An object is said to be at rest if it does not change its position with respect to its surroundings.

Rest & Motion Relative terms?
1. Introduction
- Books Name
- Mayank classes Science Book
- Publication
- Mayank classes
- Course
- CBSE Class 9
- Subject
- Science
Introduction –
• In the physical world, one of the most common phenomena is motion.
• The branch of Physics, which deals with the behavior of moving objects, is known as mechanics.
• Mechanics is further divided into two sections namely Kinematics and Dynamics.
• Kinematics deals with the study of motion without taking into account the cause of motion.
• Dynamics is concerned with the cause of motion, namely force.
Motion and Rest
• An object is said to be in motion if it changes its position with respect to its surroundings in a given time.
• An object is said to be at rest if it does not change its position with respect to its surroundings.

Rest & Motion Relative terms?
1. Introduction
Chapter 8
Motion
Introduction
• One of the most common phenomena in the physical world is motion. Mechanics is the branch of Physics that deals with the behaviour of moving objects.
• Mechanics is divided further into two sections: Kinematics and Dynamics.
• Kinematics is the study of motion without regard for the cause of motion.
• Dynamics is concerned with the source of motion, which is force.
Motion and Rest:
• An object is said to be in motion if its position in relation to its surroundings changes in a given time.
• An object is said to be at rest if its position in relation to its surroundings does not change.
• A frame of reference is another object or scene against which we compare the position of an object.
Types of Motion:
There are three types of motion:
• Translatory motion
• Rotatory motion
• Vibratory motion
Translatory Motion:
• A particle in translatory motion moves from one point in space to another. This movement may be in a straight line or in a curved path.
• Rectilinear motion is defined as motion along a straight line.
• Curvilinear motion is defined as movement along a curved path.
• As an example, consider a car driving down a straight road.
Rotatory Motion:
The particles of the body describe concentric circles around the axis of motion in rotatory motion.

Vibrational Motion:
Particles in vibratory motion move back and forth around a fixed point.
1. Introduction
- Books Name
- Yash Tyagi Coaching Science Book
- Publication
- ACERISE INDIA
- Course
- CBSE Class 9
- Subject
- Science
Font Size
We come across different substances like water that we drink; salt that we add in food for taste, milk that we drink as it provides us with calcium and other minerals, soaps that we use to wash clothes, paint that we use to colour walls and so on. These substances have different nature, different properties. They can be pure or there can be some impurities in them. Let us see what do we understand by the words pure or impure substance[11]
We come across different substances like water that we drink; salt that we add in food for taste, milk that we drink as it provides us with calcium and other minerals, soaps that we use to wash clothes, paint that we use to colour walls and so on. These substances have different nature, different properties. They can be pure or there can be some impurities in them. Let us see what do we understand by the words pure or impure substance[12]
We come across different substances like water that we drink; salt that we add in food for taste, milk that we drink as it provides us with calcium and other minerals, soaps that we use to wash clothes, paint that we use to colour walls and so on. These substances have different nature, different properties. They can be pure or there can be some impurities in them. Let us see what do we understand by the words pure or impure substance[13]
We come across different substances like water that we drink; salt that we add in food for taste, milk that we drink as it provides us with calcium and other minerals, soaps that we use to wash clothes, paint that we use to colour walls and so on. These substances have different nature, different properties. They can be pure or there can be some impurities in them. Let us see what do we understand by the words pure or impure substance[14]
We come across different substances like water that we drink; salt that we add in food for taste, milk that we drink as it provides us with calcium and other minerals, soaps that we use to wash clothes, paint that we use to colour walls and so on. These substances have different nature, different properties. They can be pure or there can be some impurities in them. Let us see what do we understand by the words pure or impure substances[15]
We come across different substances like water that we drink; salt that we add in food for taste, milk that we drink as it provides us with calcium and other minerals, soaps that we use to wash clothes, paint that we use to colour walls and so on. These substances have different nature, different properties. They can be pure or there can be some impurities in them. Let us see what do we understand by the words pure or impure substances[16]
We come across different substances like water that we drink; salt that we add in food for taste, milk that we drink as it provides us with calcium and other minerals, soaps that we use to wash clothes, paint that we use to colour walls and so on. These substances have different nature, different properties. They can be pure or there can be some impurities in them. Let us see what do we understand by the words pure or impure substances[17]
We come across different substances like water that we drink; salt that we add in food for taste, milk that we drink as it provides us with calcium and other minerals, soaps that we use to wash clothes, paint that we use to colour walls and so on. These substances have different nature, different properties. They can be pure or there can be some impurities in them. Let us see what do we understand by the words pure or impure substances[18]
We come across different substances like water that we drink; salt that we add in food for taste, milk that we drink as it provides us with calcium and other minerals, soaps that we use to wash clothes, paint that we use to colour walls and so on. These substances have different nature, different properties. They can be pure or there can be some impurities in them. Let us see what do we understand by the words pure or impure substances[19]
We come across different substances like water that we drink; salt that we add in food for taste, milk that we drink as it provides us with calcium and other minerals, soaps that we use to wash clothes, paint that we use to colour walls and so on. These substances have different nature, different properties. They can be pure or there can be some impurities in them. Let us see what do we understand by the words pure or impure substances[20]
2. Scalar and Vector Physical Quantities
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
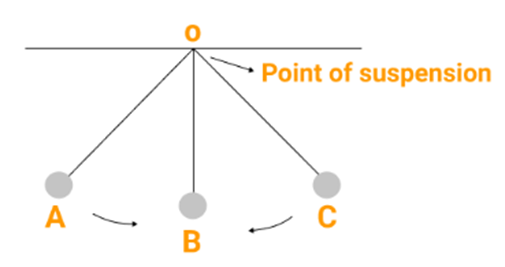
Frame of Reference - A frame of reference is another object or scene with respect to which we compare an object's position.
Objects changing positions with time with respect to the frame of reference are in motion while those which do not change position are at rest.
For example – A passenger sitting on a moving bus is at rest with respect to his co-passenger but at the same time, he is moving with the bus with respect to a person standing outside.
2. Scalar and Vector Physical Quantities
Scalar quantities
The quantities that depend upon magnitude and not the direction is called scalar quantities. They are represented as their own symbol.
Vector quantities
A physical quantity that depends upon magnitude as well as direction. They are represented by putting on their symbol.
Distance and Displacement:
Distance
• The distance travelled by a moving object is the length of the path the object takes.
• The measure of distance is a scalar quantity. The meter is the SI unit of distance.
Displacement
• It is the shortest path covered by a moving object in a specified direction from the point of reference (the initial position of the body).
• The meter is the SI unit of displacement.
• Displacement is a vector, which means that it is represented by a number with appropriate units and direction.
Difference between Distance and Displacement
|
Distance |
Displacement |
|
Distance provides the complete details of the path taken by the object |
Displacement does not provide the complete details of the path taken by the object |
|
Distance is always positive |
Displacement can be positive, negative or zero |
|
It is a scalar quantity |
It is a vector quantity |
|
The distance between two points may not be unique |
The displacement between two points is always unique |
3. Uniform and Non-Uniform Motion
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Types of Motion
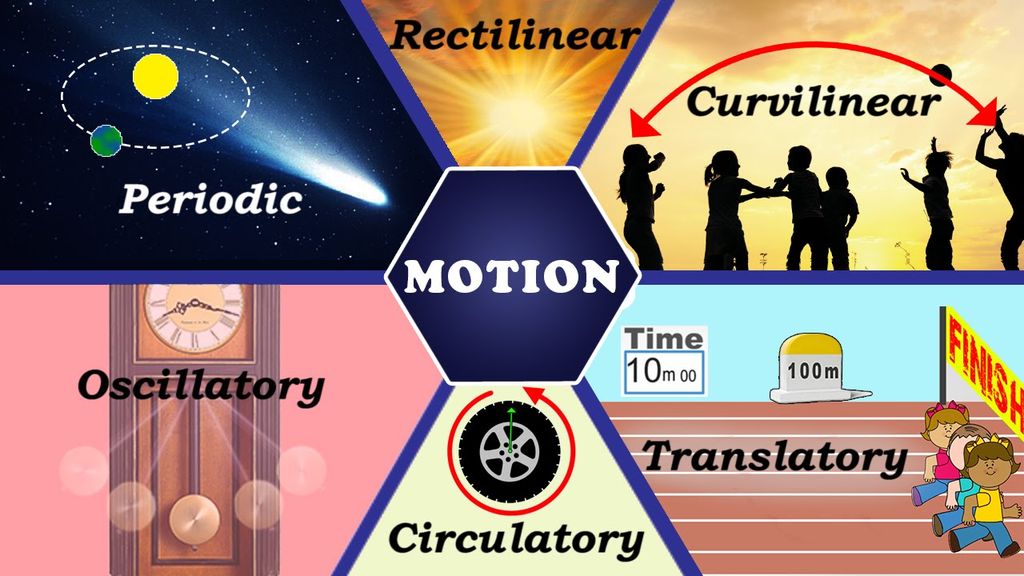
There are three types of motion:
• Translatory motion
• Rotatory motion
• Vibratory motion
Translatory Motion
• In translatory motion the particle moves from one point in space to another. This motion may be along a straight line or along a curved path.
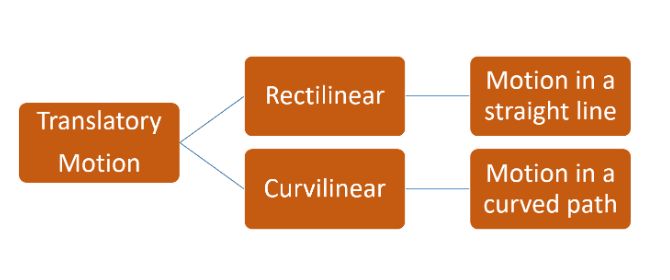
• Motion along a straight line is called rectilinear motion.
• Motion along a curved path is called curvilinear motion.
• Example: A car moving on a straight road
Curvilinear Motion
• Rotatory Motion - In rotatory motion, the particles of the body describe concentric circles about the axis of motion. Rotatory Motion
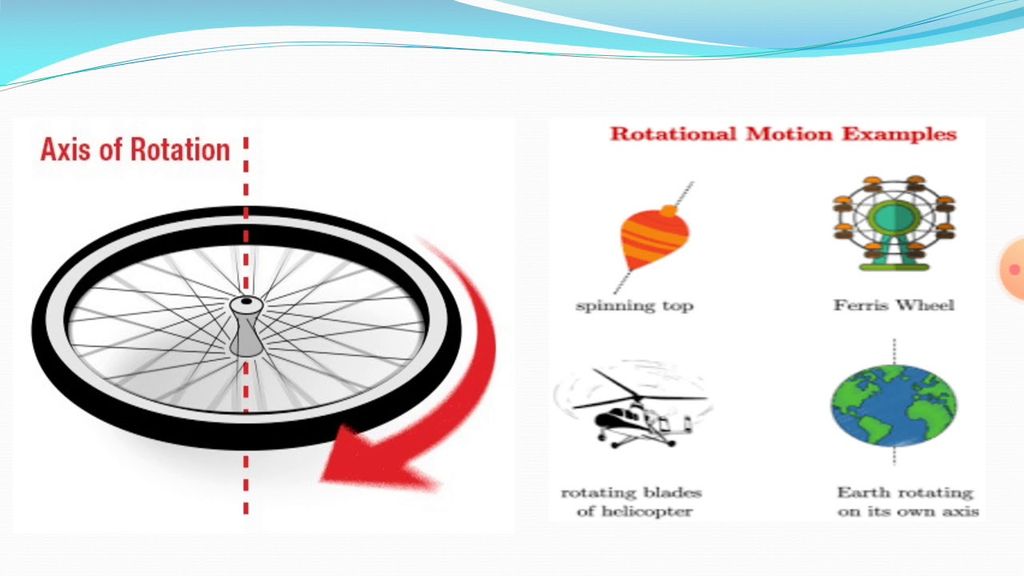
• Vibratory Motion - In vibratory motion the particles move to and fro about a fixed point.
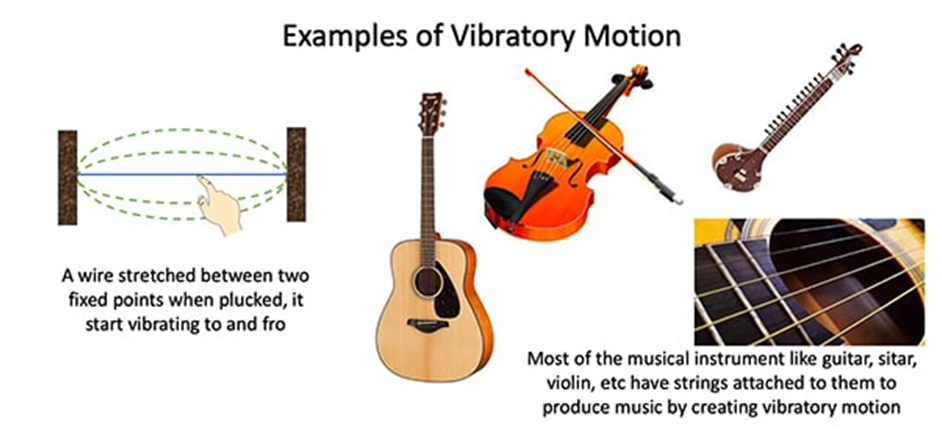
3. Uniform and Non-Uniform Motion
Motion
Uniform Motion and Non-uniform Motion:
- If the body covers equal lengths in equal time intervals, so it is assumed to have a Uniform Motion.
- If the body covers unequal distances at equal intervals or equal distances at unequal intervals, so the body is said to have Non-uniform Motion.
Speed
Speed is defined as the total distance travelled by the object in the time interval during which the motion takes place. SI unit of speed is meter per second.
Speed = Distance Travelled / Time Taken
Velocity
The velocity of a body is known as the rate of change of displacement of a body with the passage of time. The velocity of a moving object is measured in meters per second in SI units.
Acceleration
Acceleration is a measure of the change in the velocity of an object per unit of time. SI unit of acceleration is ms-2. The equation can mathematically be written as:
Uniform Acceleration
The body is said to have a uniform acceleration if it is going on a straight path and the velocity shifts (increases or decreases) by equal proportions at equal time intervals.
Non-Uniform Acceleration
A body is said to have a non-uniform acceleration if the velocity shifts (increases or decreases) by unequal proportions at unequal time frames.
4. Derivation of Equation of Motion - Graphically,Circular Motion
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Physical Quantity – The term in which results of physics can be expressed and measured.
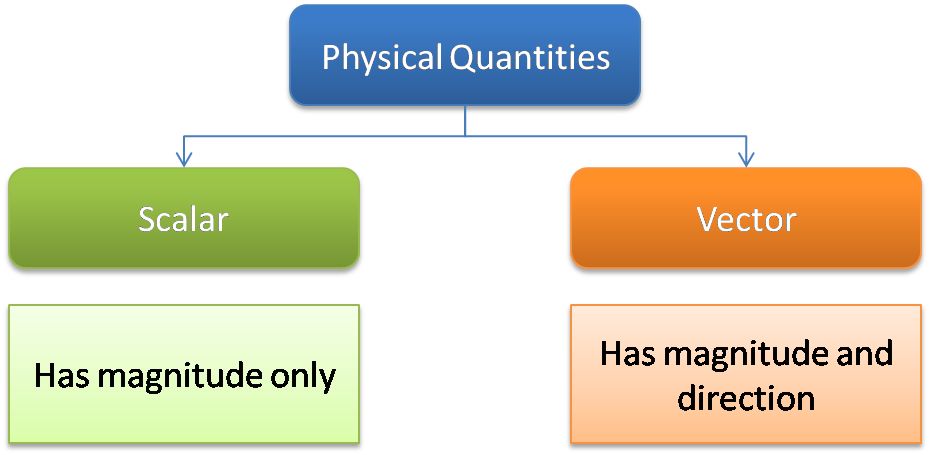
• Scalar quantity - It is the physical quantity having own magnitude but no direction.
For Example: distance, speed.
• Vector quantity - It is the physical quantity that requires both magnitude and direction.
For Example: displacement, velocity.

4. Derivation of Equation of Motion - Graphically,Circular Motion
Equation of motion by graphical methods
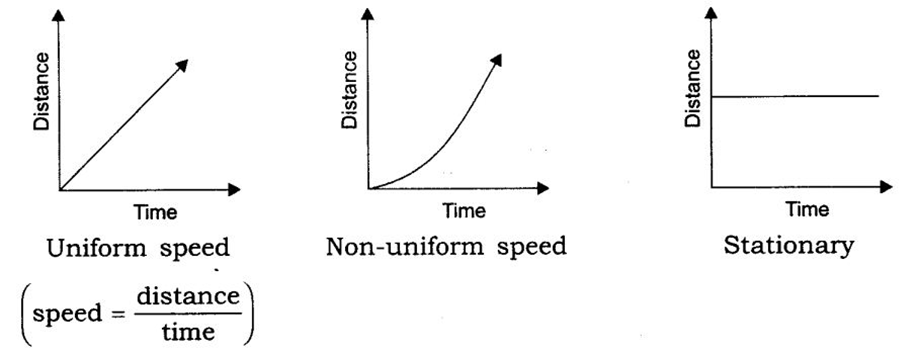
(i) Distance -Time Graph
• Distance – Time Graphs represents a change in position of the object with respect to time. The graph in case the object is stationary (means the distance is constant at all time intervals) – Straight line graph parallel to x = axis
• For a distance-time graph, time is taken on x-axis and distance is taken on the y-axis.
• For a body at rest, as the slope is zero, so the speed of the body is zero
• For a body moving with uniform speed
• For an accelerated motion., the slope of the graph is increasing with time
• For decelerated (speeding down) motion, the slope of the graph is decreasing with time.
(ii) Velocity- Time Graph
• Constant velocity is a straight-line graph, velocity is always parallel to the x-axis. When a body is moving with a uniform velocity, the slope of AB indicates zero acceleration.
• When a body starts from rest and moves with uniform acceleration, then it is greater is the slope of the v-t graph, greater will be the acceleration.
• When a body is moving with uniform acceleration and its initial velocity is not zero.
• When a body is moving with increasing acceleration, the slope gradually increases with time.
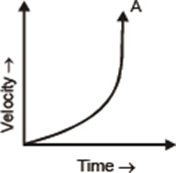
• When a body is moving with decreasing acceleration, the slope decreases with time.
• When a body is moving with uniform retardation and its initial velocity is not zero, as θ > 90°, the graph has a negative slope.
Derivations
(i)velocity-time relation:

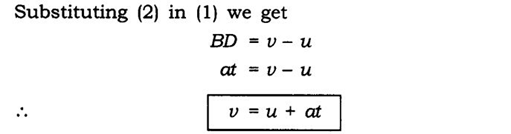
(ii) Position-time relation:
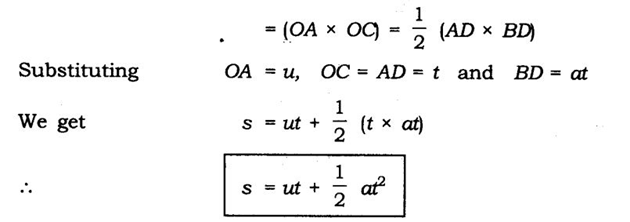
(iii) Position-velocity relation:
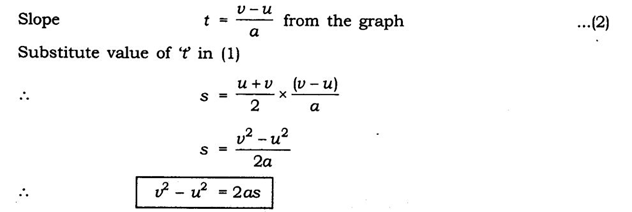
Uniform circular motion
When a body moves in a circular path with uniform speed, its motion is called uniform circular motion.
5. Equation Of Motion By Graphical Method
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Distance and Displacement
Distance -The actual path or length travelled by the object travelled by the object is called the distance.
- It is a scalar quantity.
- It is always positive.
- It can never be zero or negative.
Displacement – It is the shortest path between initial and final point.
- It is a vector quantity.
- It can be positive or negative.
- It can be zero.
Difference b\w distance and displacement
-
Example 1: A body travels in a semicircular path of radius 10 m starting its motion from point ‘A’ to point ‘B’. Calculate the distance and displacement.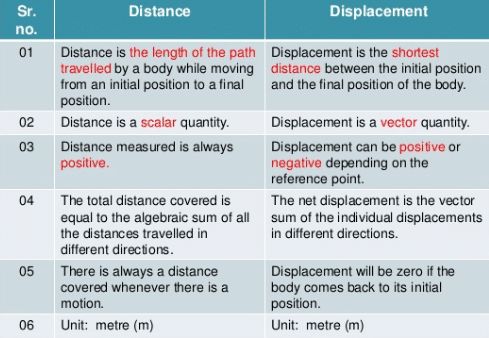
- Example 2: A body travels 4 km towards North then he turn to his right and travels another 4 km before coming to rest. Calculate (i) total distance travelled, (ii) total displacement.
UNIFORM MOTION AND NON-UNIFORM MOTION
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Uniform Motion and Non-uniform Motion
- Uniform motion - When a body covers equal distances in equal intervals of time then the body is said to describe uniform motion.
- Non uniform motion - When a body moves unequal distances in equal intervals of time or vice-versa, then the body is said to describe non-uniform motion.

NON UNIFORM MOTION
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Non uniform motion - When a body moves unequal distances in equal intervals of time or vice-versa, then the body is said to describe non-uniform motion.
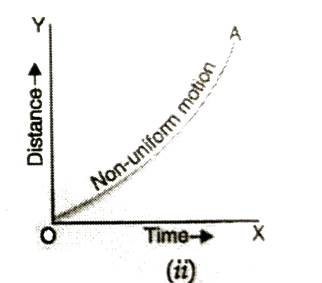
SPEED AND AVERAGE SPEED
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Speed - The measurement of distance travelled by a body per unit time is called speed.
• Speed (v) = Distance Travelled/Time Taken = s/t
• SI unit = m/s (meter/second)
Average Speed - The average speed of a body is the total distance travelled by the total time taken to cover this distance.
- Average speed= Total Distance travelled / Total Time taken
- EXAMPLE 1 - You walk 60 m at a speed of 3m/s and then run 140m at a speed of 7m/s along a straight track. Find the average speed?
- EXAMPLE 2 - What will be the speed of body in m/s and km/hr if it travels 40 kms in 5 hrs ?
AVERAGE SPEED
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Average Speed - The average speed of a body is the total distance travelled by the total time taken to cover this distance.
- Average speed= Total Distance travelled / Total Time taken
- EXAMPLE 1 - You walk 60 m at a speed of 3m/s and then run 140m at a speed of 7m/s along a straight track. Find the average speed?
- EXAMPLE 2 - What will be the speed of body in m/s and km/hr if it travels 40 kms in 5 hrs ?
VELOCITY AND AVERAGE VELOCITY
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Velocity - It is defined as the displacement of the body per unit time.
Velocity = displacement travelled / time taken
SI unit = m/s (meter/second)
Average Velocity - The average velocity of a body is the total displacement travelled by the total time taken to cover this distance.
Average velocity= Total Displacement/Total Time taken
Avg. Velocity (vavg) = (Initial velocity + Final velocity)/2 = (u+v)/2
where, u = initial velocity, v = final velocity
Example 1: During first half of a journey by a body it travel with a speed of 40 km/hr and in the next half it travels with a speed of 20 km/hr. Calculate the average speed of the whole journey.
Example 2 : If Ananya was able to travel 6 km in North in 2 hour in his car. What was her velocity?
Example 3: A car travels 20 km in first hour, 40 km in second hour and 30 km in third hour. Calculat the average speed of the train.
AVERAGE VELOCITY
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Average Velocity - The average velocity of a body is the total displacement travelled by the total time taken to cover this distance.
Average velocity= Total Displacement/Total Time taken
Avg. Velocity (vavg) = (Initial velocity + Final velocity)/2 = (u+v)/2
where, u = initial velocity, v = final velocity
Example 1: During first half of a journey by a body it travel with a speed of 40 km/hr and in the next half it travels with a speed of 20 km/hr. Calculate the average speed of the whole journey.
Example 2 : If Ananya was able to travel 6 km in North in 2 hour in his car. What was her velocity?
Example 3: A car travels 20 km in first hour, 40 km in second hour and 30 km in third hour. Calculat the average speed of the train.
ACCELERATION/ RETARDATION
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Acceleration - Acceleration is seen in non-uniform motion and it can be defined as the rate of change of velocity with time.
- Acceleration (a) = Change in velocity/Time = (v-u)/t
where, v = final velocity, u = initial velocity
- If v > u, then ‘a’ will be positive (+ve).
Retardation/Deceleration - Deceleration is seen in non-uniform motion during decrease in velocity with time. It has same definition as acceleration
- Deceleration (a') = Change in velocity/Time = (v-u)/t
- Here, v < u, ‘a’ = negative (-ve).
- It is a vector quantity.
- SI unit – m/s2 ( meter per second square)
Example 1: A car speed increases from 40 km/hr to 60 km/hr in 5 sec. Calculate the acceleration of car.
Example 2: A car travelling with a speed of 20 km/hr comes into rest in 0.5 hrs. What will be the valu of its retardation?
EXAMPLE 3 : If the velocity of the car reduced to 80 m/s from 120 m/s in 8 seconds on applying breaks . Calculate its acceleration.
6. Uniform Circular Motion
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
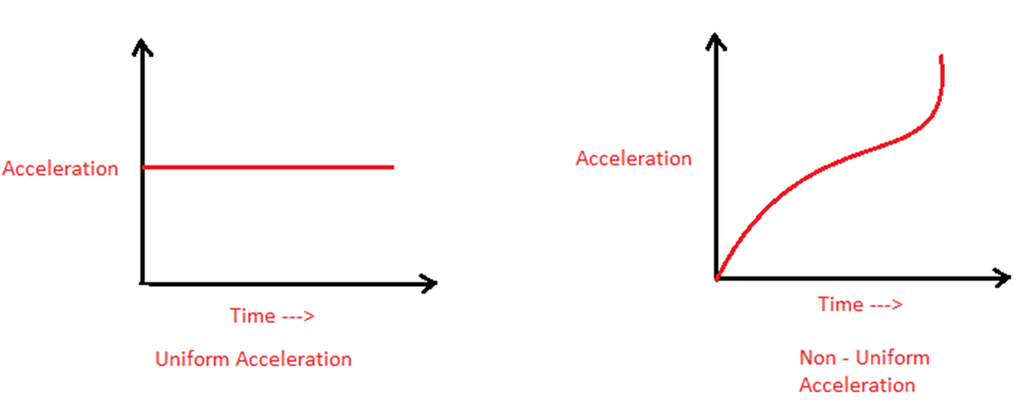
Uniform Acceleration - If the change in velocity in equal intervals of time is always the same, then the object is said to be moving with uniform acceleration.
Example: a body falling from a height towards the surface of the earth.
Non-uniform or Variable Acceleration- If the change in velocity in equal intervals of time is not the same, then the object is said to be moving with variable acceleration.
Example - A ball thrown vertically upwards is moving with a negative acceleration as the velocity decreases with time.
GRAPHS OF MOTION
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Graphs for Motion -
1) Distance-time graphs (s-t graphs)
a) When the object is stationary or at rest -
The distance time graph for stationary object is the line parallel to time axis.
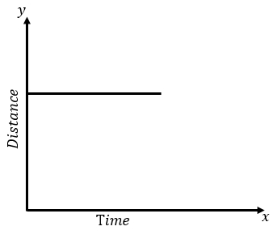
b) When object is in uniform motion -
The distance time graph for the object moving in uniform motion is the straight line inclined to time axis.
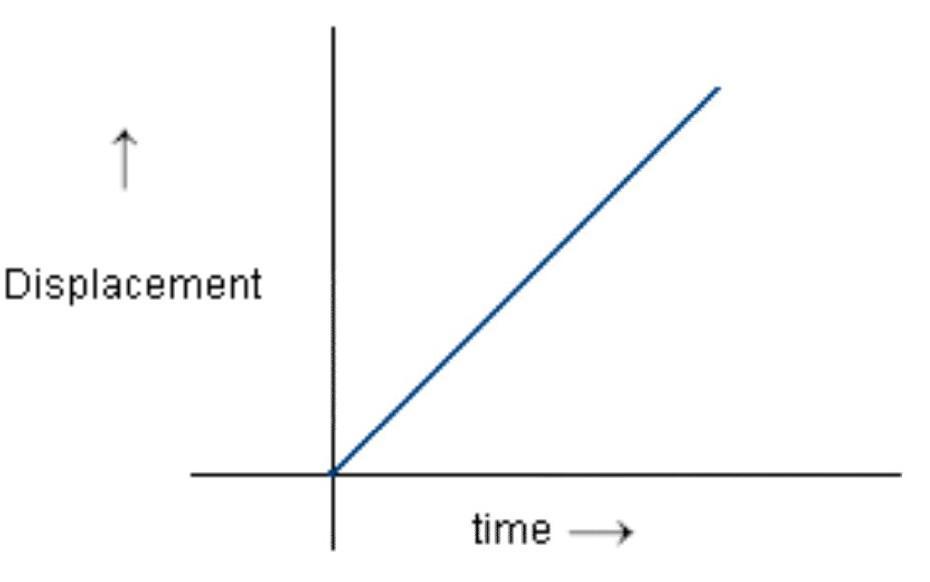
C) When object is in non-uniform motion -
The distance time graph for object moving in non -uniform motion is the curved line.
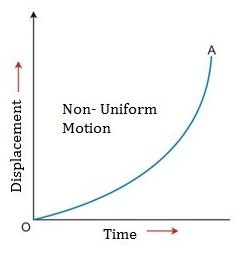
Important results of distance time graphs -
1) area under curve of s-t graph = displacement/distance travelled by the object
2) slope of s-t graph = velocity of the object
Velocity time graphs (v-t graphs)
a) When object is moving with constant speed -
The velocity time graph for an object moving with constant/same speed is given by a straight line parallel to time axis.
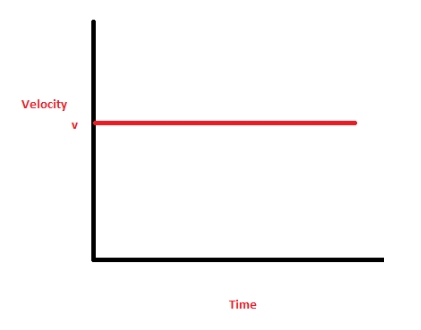
b) When object is in uniform motion -
The velocity tiem graph for an object in uniform motion is the straight line inclined to time axis.
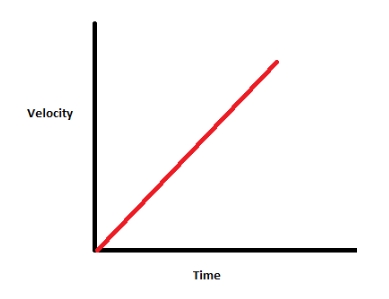
C) When object is in non-uniform motion -
The distance time graph for object moving in non -uniform motion is the curved line.
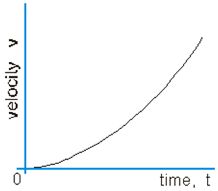
Important results of velocity time graphs -
1) area under curve of v-t graph = displacement/distance travelled by the object
2) slope of v-t graph = acceleration of the object
EQUATIONS OF MOTION AND DERIVATION OF EQUATIONS BY GRAPHICAL METHOD
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
Definition of Equations of Motion
Equations of motion, in physics, are defined as equations that describe the behaviour of a physical system in terms of its motion as a function of time.
There are three equations of motion that can be used to derive components such as displacement(s), velocity (initial and final), time(t) and acceleration(a). The following are the three equation of motion:
- First Equation of Motion : v=u+at
- Second Equation of Motion : s=ut+1/2 at2
- Third Equation of Motion : v2=u2+2as
DERIVATION OF FIRST EQUATION OF MOTION ( V = u+at )
Consider a body of mass “m” having initial velocity “u”. Let after time “t” its final velocity becomes “v” due to uniform acceleration “a”.
Now as we know that,
Acceleration = change in velocity/Time taken Acceleration = Final velocity-Initial velocity / time taken
a = v-u/t
=> at = v-u
or v = u + at
This is the first equation of motion.
DERIVATION OF SECOND EQUATION OF MOTION (S=ut+1/2 at2 )
Consider a body of mass “m” having initial velocity “u”. Let after time “t” its final velocity becomes “v” due to uniform acceleration “a”. Let the distance travelled by the body be “s”.
Now As we know that,
Distance = Average velocity X Time
Also, Average velocity = u+v/2
Distance (s) = ( u+v ) *t/2 …….eq.(1)
Again we know that, v = u + at
By substituting this value of “v” in eq.(1), we get
Distance(s) = (u+u+at) *t/2
=> s = (2u+at)* t/2
=> s = 2ut/2+at2/2
=>s = ut+ at2/2
or s = ut + 1/2 at2
This is the second equation of motion.
DERIVATION OF THIRD EQUATION OF MOTION (V2 = u2+2as)
Consider a body of mass “m” having initial velocity “u”. Let after time “t” its final velocity becomes “v” due to uniform acceleration “a”. Let the distance travelled by body be “s”.
Displacement=(Initial Velocity+Final Velocity)×t/2
Substituting the standard notations, the above equation becomes
s=(u+v)×t/2
From the first equation of motion, we know that
v=u+at
Rearranging the above formula, we get
t=v−u/a
Substituting the value of ‘t’ in the displacement formula, we get
s=(v+u)/2 *(v−u)/a
s=(v2 - u2)/2a
2as= v2 - u2
Rearranging, we get
v2 – u2= 2as This is the third equation of motion.
UNIFORM CIRCULAR MOTION
- Books Name
- Science Made Easy Science Book
- Publication
- Science Made Easy
- Course
- CBSE Class 9
- Subject
- Science
What is Uniform Circular Motion?
The movement of a body following a circular path is called a circular motion. Now, the motion of a body moving with constant speed along a circular path is called Uniform Circular Motion. Here, the speed is constant but the velocity changes.
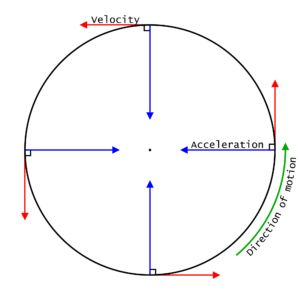
NOTE -
So if a particle is moving in a uniform circular motion:
1) Its speed is constant
2) Velocity is changing at every instant
Uniform Circular Motion Examples
Following are the examples of uniform circular motion:
- Motion of artificial satellites around the earth is an example of uniform circular motion. The gravitational force from the earth makes the satellites stay in the circular orbit around the earth.
- The motion of electrons around its nucleus.
- The motion of blades of the windmills.
- The tip of second’s hand of a watch with circular dial shows uniform circular motion.
Formula for veocity in UCM -
V=2πR/T
where R is radius of circle, T is time taken

 Science Made Easy
Science Made Easy
 ACERISE INDIA
ACERISE INDIA
