Correct Measurement of Length

Measurement  of Area
The amount of surface covered by the object is called its area. The measurement of area counts two dimensions. The SI unit of area is square metre, represented as m². This is the area covered by a square whose length and breadth are 1 m each. 

The area of regular surfaces (squares, rectangles etc.) can be measured by using the following formula: 
area of a square = length × length 
area of a rectangle = length × breadth

Ex.1    How many m²  are equal to 1 cm² area?
Sol.     1 m² = 1 m × 1 m 
        = (100) cm × (100) cm
        = (10000) cm² = 104 cm²

Measurement  of volume
The amount of space occupied by an object is its volume. The SI unit of volume is the cubic metre represented as m³ .
The litre (represented as l) is an important unit of volume used in the everyday life.
1 litre = 1000 ml    
1 m³ = 1000 litres
The litre is also known as 1000 cm³.
Since 1 litre = (1/1000) m³.

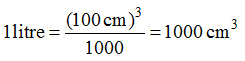
The volume of a liquid is more often expressed in millilitres. 

The volume of a solid that has a regular shape can be calculated using a mathematical formula. The formula for determining the volumes of some regular solids are: 
Volume of a cube = l³ 
where l is the length of the side of the cube. 
Volume of a cuboid = l × b × h 
where l is the length, b is the breadth, and h is the height of the cuboid. 
e.g.    Volume of a cube of side 1 m 
        = 1m × 1m × 1m 
        = 1 × 1 × 1 m³ 
        = 1 m³ 

Volume of a cube of side 1 cm 
        = 1 cm × 1 cm × 1 cm 
        = 1 × 1 × 1 cm³ 
        = 1 cm³ 
    Volume of a cube with sides 10 cm 
        = 10 × 10 × 10 cm³ = 1000 cm³ 

    Volume of a cube with sides 1 dm 
        = 1 × 1 × 1 dm³ = 1 dm³ 
        1000 cm³ = 1 dm³ 
        1 litre = 1000 ml 
        = 1000 ml 
    or     1 cm³ = 1 ml 

Ex.2    Convert : 
        (i) 54 km/hr = ? m/s                (ii) 15 m/s = ? km/hr    
        (iii) 30 km/cm = ? m/mm        (iv) 12 m/km = ? mm/cm

Correct Measurement of Length

Each metre (m) is divided into 100 equal divisions, called centimetres (cm). Each centimeter has ten equal divisions, called millimeters (mm).

Thus,

• 1 m = 100 cm
• 1 cm = 10 mm

For measuring large distances, metre is not a convenient unit.

We define a larger unit of length. It is called kilometer (km).

• 1 km = 1000 m.

Simple multiples of units: Units that are used for the measurement of larger distances are the multiples of SI units.

For example: deca, hecto, kilo.

• 1 decameter = 10 m
• 1 hectometer = 100 m
• 1 kilometer = 1000 m

Submultiples of units: Units used for measuring smaller distances are the submultiples of SI units.

For example, milli, centi, deci.

• 1 m = 10 decimetre
• 1 m = 100 centimeter
• 1 m = 1000 millimeter

Correct Way to Use a Meter Scale

•  Keep the scale in contact with the object to be measured.

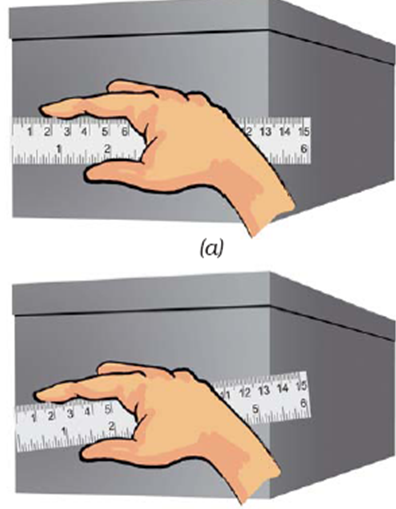
If scales are broken or the zero mark is not visible, it can lead to a zero error. Then measuring from a different mark must be carried out.

• Then, avoid taking measurements from zero mark.
• Use any other full mark of the scale, say 1.0 cm.
• Subtract the reading of this mark from the reading at the other end. For example, in Fig. 10.3 (6), the reading at starting mark is 1.0 cm and at the other end it is 6.5 cm. Therefore, the length of the object is (6.5 – 1.0) cm = 5.5 cm.
• The correct reading will be obtained by subtracting the value from the full mark considered as zero.
• Measurement with a scale with broken ends

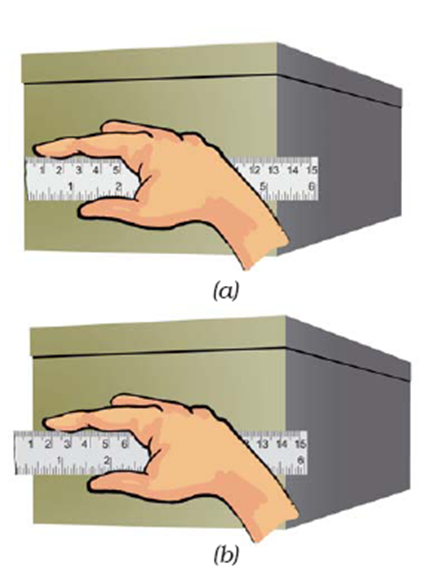
While measuring the eye must be exactly above the point where the measurement is to be taken, to avoid parallax errors.

• Start measuring from the 0 mark of the scale.
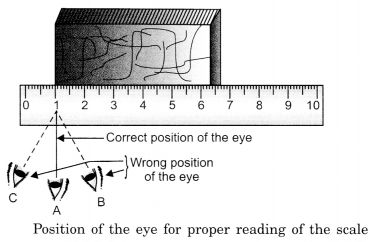
• To avoid taking incorrect measurements the eye position should be correct. Consider the following figure:

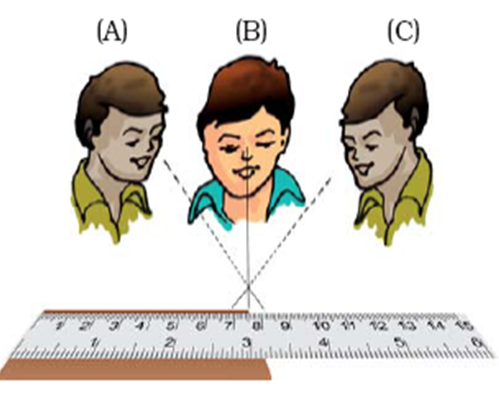
The eye position in the centre is correct to get an accurate measurement, while the ones in the left and right direction will give some error in measurement.

• Correct position of the eye is also important for making measurement. Your eye must be exactly above the point where the measurement is to be taken as shown in Fig. 10.4. Position ‘A’ is the correct position of the eye. Note that from position A’, the reading is 1.0 cm. From positions ‘B’ and ‘C’, the readings may be different.
• The eye position in the centre is correct to get an accurate measurement, while the ones in the left and right direction will give some error in measurement.
• Correct position of the eye is also important for making measurement. Your eye must be exactly above the point where the measurement is to be taken as shown in Fig. 10.4. Position ‘A’ is the correct position of the eye. Note that from position A’, the reading is 1.0 cm. From positions ‘B’ and ‘C’, the readings may be different.

  

Least count: A scale is marked in centimetres and millimeters. With the scales of this kind we can measure correctly up to one millimeter, that is one-tenth of a centimeter. This is called the least count of a (15 cm) scale.