- Books Name
- CBSE Class 6 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 6
- Subject
- Mathmatics
Solid Figures
A figure which have three dimensions as length, breadth and height is not a plane figure and we can not draw such figures on black board exactly. These three dimensional figures are called solids for example Cube, cuboid, cylinder cone, sphere etc. are some three dimensional figures. In this section we will learn how we determine the surface area of such solids.
1. Cuboid: A solid like an ordinary brick, each face of which is rectangle is called a rectangular solid or cuboid.
A cuboid has 6 rectangular plane surfaces, called faces. It has 12 edges and 8 vertices. If a cuboid is l cm long b cm broad and h cm high, then
(i) Total Surface Area of Cuboid: We know that the outer surface of cuboid is made up of six rectangles and the area of rectangle can be found by multiplying length by breadth.
Area of I rectangle = l × h
Area of opposite of I rectangle = l × h
Area of II rectangle = b × h
Area of opposite of II rectangle = b × h
Area of III rectangle = l × b
Area of opposite of III rectangle = l × b
Surface Area of a cuboid = Area of 6 rectangles = lb + lb + bh + bh + hl + hl = 2lb + 2bh + 2hl = 2(lb + bh + hl)
Total surface area of a cuboid = 2(lb + bh + hl)
(ii) Lateral surface area of cuboid = 2(l + b) × h cm2
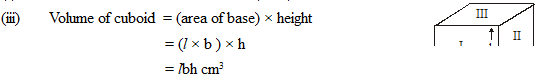
2. Cube: It is a particular case of a cuboid where length = breadth = height. Each edge of a cube is called its side.
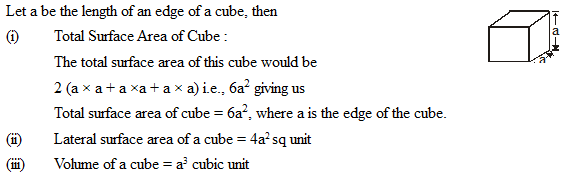
Ex.1 If length and breadth of a cuboid is 4 cm and 6 cm and having total surface area is 208 cm2 then find the height of cuboid.
Sol. Let L = 4 cm, B = 6 cm
Total surface area of cuboid = 2(LB + BH + HL)
208 = 2 [4 ´ 6 + 6 ´ H + H ´ 4]
208 = 2 [24 + 6 ´ H + H ´ 4]
208 = 2 [24 + 10H]
24 + 10 H = = 104
10 H = 104 – 24 = 80
H = = 8
there for height of the cuboid = 8 cm
Ex.2 A cube of 9 cm edge is immersed completely in a rectangular vessel containing water. If the dimensions of the base are 15 cm and 12 cm. Find the rise in water level in the vessel.
Sol. We have
Edge of the given cube = 9 cm.
∴ Volume of the cube = (9)3 cm3 = 729 cm3
If the cube is immersed in the vessel, then the water level rises. Let the rise in water level be h cm.
Clearly,
Volume of the cube = Volume of the water replaced by it.


 Param Publication
Param Publication
