Chapter 2: Relations and Functions

Chapter 2

Relation and Function

Cartesian Product / Product Simply:

After French philosopher, mathematician and Scientists René Descartes (1596-1650),whose formulation of analytic geometry gave rise to the concept.

In 17^th century the invention of Cartesian coordinates system by Rene Descartes( Latin name: cartesius) revolutionized mathematics by providing the first systematic link between  Euclidean Geometry and Algebra

Who invented the Cartesian product?

René Descartes invented the Cartesian product. It derives the name from the same person. René formulated analytic geometry which helped in the origination of this concept which we further generalize in terms of direct product.

An ordered pair means that two elements are taken from each set.’

 For two non-empty sets (say A & B), the first element of the pair is from one set A and the second element is taken from the second set B.

If {a,b} is a set consisting of the elements of a,b, it is called pair.

If we specify a to be the first element and b to be the second element , then we call {a,b} an order pair and Write it as (a,b).

Cartesian Products of Sets:

Let A and B be the two sets such that A is a set of three colors of tables and B is a set of three colors of chairs objects, i.e.,

A = {brown, green, yellow}

B = {red, blue, purple},

Let’s find the number of pairs of colored objects that we can make from a set of tables and chairs in different combinations. They can be paired as given below:

(brown, red), (brown, blue), (brown, purple), (green, red), (green, blue), (green, purple), (yellow, red), (yellow, blue), (yellow, purple)

There are nine such pairs in the Cartesian product since three elements are there in each of the defined sets A and B. The above-ordered pairs represent the definition for the Cartesian product of sets given. This product is denoted by “A × B”.

Suppose there are two non-empty sets A and B.

So, the Cartesian product of A and B is the set of all ordered pairs of elements from A and B.

i.e., A × B = {(a , b) : a ∊ A, b ∊ B}

Example: Let A = {a_1,a_2,a₃,a₄} and B = {b₁,b₂}

Then, The Cartesian product of A and B will be;

A × B = {(a_1,b₁₎, (a_2,b₁),( a_3,b₁),( a_4,b₁).( a_1,b₂),( a_2,b₂),( a_3,b₂),( a_4,b₂ )}

Example: Let us say, A = {1,2} and B = { a,b,c}

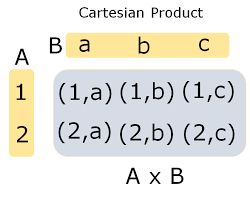
Therefore, A × B = {(1,a),(1,b),(1,c),(2,a),(2,b),(2,c)}.

This set has 8 ordered pairs. We can also represent it as in a tabular form.

Note: Two ordered pair X and Y are equal, if and only if the corresponding first elements and second elements are equal.

Example: Suppose, A = {cow, horse} B = {egg, juice}

 then, A×B = {(cow, egg), (horse, juice), (cow, juice), (horse, egg)}

If either of the two sets is a null set, i.e., either A = Φ or B = Φ, then, A × B = Φ i.e., A × B will also be a null set

Number of Ordered Pairs

For two non-empty sets, A and B. If the number of elements of A is p

 i.e., n(A) = p & that of B is q

 i.e., n(B) = q,

then the number of ordered pairs in Cartesian product will be n(A × B) = n(A) × n(B) = pq.

Properties:

1. The Cartesian Product is non-commutative: A × B ≠ B × A.
2. The cardinality of the Cartesian Product is defined as the number of elements in A × B and is equal to the product of cardinality of both sets:

|A × B| = |A| * |B|

3. A × B = ∅, if either A = ∅ or B = ∅
4. If (x,y) = (a,b) ,then x=a , y=b
5. A×B=B×A, if only A=B
6. The Cartesian product is associative:

(A×B)×C=A×(B×C). It means the Cartesian product of the three-set is the same, i.e., it doesn’t depend upon which bracket is multiplied first as the final result will be the same.

7. Distributive property over a set intersection:

A×(B∩C)=(A×B)∩(A×C)

8.  Distributive property over set union:

A×(B∪C)=(A×B)∪(A×C)

9.  If A⊆B, then A×C⊆B×C for any set C.
10. AxBxC  = {(a,b,c) : aÎA, bÎ B ,cÎ C}

Here (a,b,c) is called ordered triplet.

Solved Examples:

1. Let A = {–1, 2, 3} and B = {1, 3}. Determine
(i) A × B

(ii) B × A
(iii) B × B

(iv) A × A

Solution:

According to the question,

A = {–1, 2, 3} and B = {1, 3}

(i) A × B

{–1, 2, 3} × {1, 3}

So, A × B = {(–1, 1), (–1, 3), (2, 1), (2, 3), (3, 1), (3, 3)}

Hence, the Cartesian product = {(–1, 1), (–1, 3), (2, 1), (2, 3), (3, 1), (3, 3)}

(ii) B × A.

{1, 3} × {–1, 2, 3}

So, B × A = {(1, –1), (1, 2), (1, 3), (3, –1), (3, 2), (3, 3)}

Hence, the Cartesian product = {(1, –1), (1, 2), (1, 3), (3, –1), (3, 2), (3, 3)}

(iii) B × B

{1, 3} ×{1, 3}

So, B × B = {(1, 1), (1, 3), (3, 1), (3, 3)}

Hence, the Cartesian product = {(1, 1), (1, 3), (3, 1), (3, 3)}

(iv) A × A

{–1, 2, 3} × {–1, 2, 3}

So, A × A = {(–1, –1), (–1, 2), (–1, 3), (2, –1), (2, 2), (2, 3), (3, –1), (3, 2), (3, 3)}

Hence,

the Cartesian product ={(–1, –1), (–1, 2), (–1, 3), (2, –1), (2, 2), (2, 3), (3, –1), (3, 2), (3, 3)}

2. If P = {x : x < 3, x ∈ N}, Q = {x : x ≤ 2, x ∈ W}. Find (P ∪ Q) × (P ∩ Q), where W is the set of whole numbers.

Solution:

According to the question,

P = {x: x < 3, x ∈N}, Q = {x : x ≤ 2, x ∈W} where W is the set of whole numbers

P = {1, 2}

Q = {0, 1, 2}

Now

(P∪Q) = {1, 2}∪{0, 1, 2} = {0, 1, 2}

And,

(P∩Q) = {1, 2}∩{0, 1, 2} = {1, 2}

We need to find the Cartesian product of (P∪Q) = {0, 1, 2} and (P∩Q) = {1, 2}

So,

(P∪Q) × (P∩Q) = {0, 1, 2} × {1, 2}

= {(0, 1), (0, 2), (1, 1), (1, 2), (2, 1), (2, 2)}

Hence, the Cartesian product = {(0, 1), (0, 2), (1, 1), (1, 2), (2, 1), (2, 2)}

3. If A = {x : x ∈ W, x < 2}, B = {x : x ∈ N, 1 < x < 5}, C = {3, 5} find
(i) A × (B ∩ C)
(ii) A × (B ∪ C)

Solution:

According to the question,

A = {x: x ∈ W, x < 2}, B = {x : x ∈N, 1 < x < 5} C = {3, 5}; W is the set of whole numbers

A = {x: x ∈ W, x < 2} = {0, 1}

B = {x : x ∈N, 1 < x < 5} = {2, 3, 4}

(i)

(B∩C) = {2, 3, 4} ∩ {3, 5}

(B∩C) = {3}

A × (B∩C) = {0, 1} × {3} = {(0, 3), (1, 3)}

Hence, the Cartesian product = {(0, 3), (1, 3)}

(ii)

(B∪C) = {2, 3, 4} ∪ {3, 5}

(B∪C) = {2, 3, 4, 5}

A × (B∪C) = {0, 1} × {2, 3, 4, 5} = {(0, 2), (0, 3), (0, 4), (0, 5), (1, 2), (1, 3), (1, 4), (1, 5)}

Hence, the Cartesian product = {(0, 2), (0, 3), (0, 4), (0, 5), (1, 2), (1, 3), (1, 4), (1, 5)}

 

4. : The Cartesian product A × A has 9 elements among which are found (–1, 0) and (0,1). Find the set A and the remaining elements of A × A.

Solution:

We know that,

If n(A) = p and n(B) = q, then n(A × B) = pq

From the given,

n(A × A) = 9

n(A) × n(A) = 9,

n(A) = 3 ……(i)

The ordered pairs (-1, 0) and (0, 1) are two of the nine elements of A × A.

Therefore, A × A = {(a, a) : a ∈ A}

Hence, -1, 0, 1 are the elemets of A. …..(ii)

From (i) and (ii),

A = {-1, 0, 1}

The remaining elements of set A × A are (-1, -1), (-1, 1), (0, -1), (0, 0), (1, -1), (1, 0) and (1, 1).

Relations and Types of Relations

Relation:

Relation is association between two well-defined  objects.

Relation  in real life give us the link between any two objects or entities. In our daily life, we come across many patterns and links that characterize relations such as a relation of a father and a son, brother and sister, etc.

Relations can be represented in different forms such as arrow representation, algebraic form, set-builder form, graphically, roster form, and tabular form. 

Definition:

Let A and B be two non empty sets.

Then R  :  A ® B  is said to be a relation if R Í AxB .

The element of A (first element) of AxB in the relation is called Domain or Pre-image of relation R.

The element of B (second element) of AxB in the relation is called Range or image of relation R.

The whole B set of AxB in the relation is called Codomain of relation R.

Range Í Codomain

Example : Define a relation R from A to A = {1, 2, 3, 4, 5, 6} as R = {(x, y) : y = x + 1}. Determine the domain, codomain and range of R.

Solution: We can see that A = {1, 2, 3, 4, 5, 6} is the domain and codomain of R.

To determine the range, we determine the values of y for each value of x, that is, when x = 1, 2, 3, 4, 5, 6

• • x = 1, y = 1 + 1 = 2;
  • x = 2, y = 2 + 1 = 3;
  • x = 3, y = 3 + 1 = 4;
  • x = 4, y = 4 + 1 = 5;
  • x = 5, y = 5 + 1 = 6;
  • x = 6, y = 6 + 1 = 7.

Since 7 does not belong to A and the relation R is defined on A, hence, x = 6 has no image in A.

Therefore range of R = {2, 3, 4, 5, 6}

Answer: Domain = Codomain = {1, 2, 3, 4, 5, 6}, Range = {2, 3, 4, 5, 6}

Types of Relations

Given below is a list of different types of relations:

1. Empty Relation
2. Universal Relation
3. Identity Relation
4. Inverse Relation
5. Reflexive Relation
6. Symmetric Relation
7. Transitive Relation
8. Equivalence Relation

1) Empty Relation - A relation is an empty relation if it has no elements, that is, no element of set A is mapped or linked to any element of A. It is denoted by R = ∅.

For example, if set A = {1, 2, 3} then, one of the void relations can be R = {x, y} where, |x – y| = 8. For empty relation,

R = φ ⊂ A × A

2) Universal Relation - A relation R in a set A is a universal relation if each element of A is related to every element of A, i.e., R = A × A. It is called the full relation.

Consider set A = {a, b, c}. Now one of the universal relations will be R = {x, y} where, |x – y| ≥ 0. For universal relation,

R = A × A

3) Identity Relation - A relation R on A is said to be an identity relation if each element of A is related to itself, that is, R = {(a, a) : for all a ∈ A}

 For example, in a set A = {a, b, c}, the identity relation will be I = {a, a}, {b, b}, {c, c}. For identity relation,

I = {(a, a), a ∈ A}

4) Inverse Relation - Define R to be a relation from set P to set Q i.e., R ∈ P × Q. The relation R-1 is said to be an Inverse relation if R-1 from set Q to P is denoted by R^-1 = {(q, p): (p, q) ∈ R}.

For example if set A = {(a, b), (c, d)}, then inverse relation will be R^-1 = {(b, a), (d, c)}. So, for an inverse relation,

R^-1 = {(b, a): (a, b) ∈ R}

5) Reflexive Relation - A binary relation R defined on a set A is said to be reflexive if, for every element a ∈ A, we have aRa, that is, (a, a) ∈ R.

 For example, consider a set A = {1, 2,}. Now an example of reflexive relation will be R = {(1, 1), (2, 2), (1, 2), (2, 1)}. The reflexive relation is given by-

(a, a) ∈ R

6) Symmetric Relation - A binary relation R defined on a set A is said to be symmetric if and only if, for elements a, b ∈ A, we have aRb, that is, (a, b) ∈ R, then we must have bRa, that is, (b, a) ∈ R.

 An example of symmetric relation will be R = {(1, 2), (2, 1)} for a set A = {1, 2}. So, for a symmetric relation,

aRb ⇒ bRa, ∀ a, b ∈ A

Example: For the set P={a,b}, the relation R={(a,b),(b,a)} is called symmetric relation, where a,b∈P.

7) Transitive Relation - A relation R is transitive if and only if (a, b) ∈ R and (b, c) ∈ R ⇒ (a, c) ∈ R for a, b, c ∈ A

Example: For the set A ={a,b,c}, the relation R={(a,b),(b,c),(a,c)} is called transitive relation, where a,b,c∈ A.

8) Equivalence Relation - A relation R defined on a set A is said to be an equivalence relation if and only if it is reflexive, symmetric and transitive.

Conditions:

1. If the relation (R) is reflexive, then all the elements of set A are mapped with itself, such that for every x∈ A , then (x,x)∈R.

2. The relation (R) is symmetric on set A, if (x,y)∈R, then (y,x)∈R, such that a,b∈ A.

3. The relation R on set A, if (x,y)∈R and (y,z)∈R, then (x,z)∈R, for all a,b,c∈ A is called transitive relation

Other Types of Relations:

The other types of relations based on mapping of two sets are given as follows:

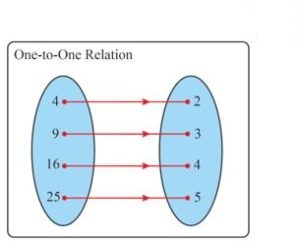
1) One to One Relations

A relation is said to be a One to One relation if all the distinct elements of one set are related or mapped to distinct elements of another set.

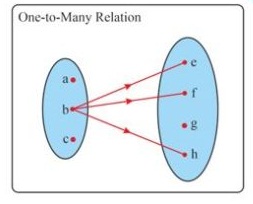
2) One to Many Relations

A relation is said to be One to Many relations if the one element of first set is mapped to more than one element second set.

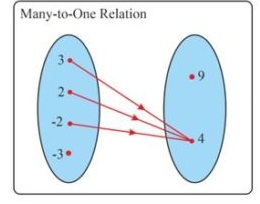
3) Many to One Relation

A relation is said to be Many to One relation if  the more than one element of first set is mapped to one element second set.

4) Many to Many Relation

A relation is said to be Many to Many relation if  the more than one element of first set is mapped to more than one element second set.

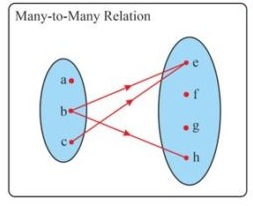
Solved Examples:

Q.1. Let A be the set of two male persons in a family. R be a relation defined onset A is “is a brother of”, check whether R is symmetric or not?

Ans:

Let a,b are two persons in a family, then a,b∈A.

The given relation on set “is a brother of”.

If a is the brother of b, then b is also the brother of a.

R={(a,b),(b,a)}

Hence, the relation R is symmetric.

Q.2. Find the inverse relation of R={(1,2),(3,4),(5,6)}.

Ans:

Given relation is R={(1,2),(3,4),(5,6)}.

Consider R={(a,b):a∈P,b∈Q}. be the relation from set P to set Q, then the relation from set Q to set P is known as inverse relation, such that R–1:Q→P={(a,b):(a,b)∈R}.

So, inverse relation is obtained by taking the reverse of the given ordered pairs.

R–1:{(2,1),(4,3),(6,5)}

Q.3. Find the identity relation on the set P={x,y,z}.

Ans:

We know that the relation (I) is identity, then all the elements of set P are related with itself, such that for every a∈P, then (a,a)∈I.

Given set is P={x,y,z}

Then the identity relation is given by I={(x,x),(y,y),(z,z)}.

Q.4. Let P={1,2,3},R be a relation defined on set P as “is greater than” and R={(2,1),(3,2),(3,1)}. Verify R is transitive.

Ans:

Given set P={1,2,3},

Let P={1,2,3}, then we have

(b,a)=(2,1)→2 is greater than 1.

(c,b)=(3,2)→3 is greater than 2.

(c,a)=(3,1)→3 is greater than 1.

Thus in a transitive relation, if (x,y)∈R,(y,z)∈R, then (x,z)∈R.

So, the relation R={(2,1),(3,2),(3,1)} is transitive.

Q.5. Let set A contains the bag of red balls. Then the relation R of getting white balls from the bag of red balls is what type of relation?

Ans:

Given set A contains the bag contains the red balls. From the bag of red balls, relation R of getting the white ball is not possible. So, the given relation is an empty relation.

Q6. Given R = {(x, y) : x, y ∈ W, x² + y² = 25}. Find the domain and Range of R.

Ans:

According to the question,

R = {(x, y) : x, y ∈W, x² + y² = 25}

R = {(0,5), (3,4), (4, 3), (5,0)}

The domain of R consists of all the first elements of all the ordered pairs of R.

Domain of R = {0, 3, 4, 5}

The range of R contains all the second elements of all the ordered pairs of R.

Range of R = {5, 4, 3, 0}

Q7. If R₁ = {(x, y) | y = 2x + 7, where x ∈ R and – 5 ≤ x ≤ 5} is a relation. Then find the domain and Range of R₁.

Ans:

According to the question,

R₁ = {(x, y) | y = 2x + 7, where x ∈R and – 5 ≤ x ≤ 5} is a relation

The domain of R₁ consists of all the first elements of all the ordered pairs of R₁, i.e., x,

It is also given – 5 ≤ x ≤ 5.

Therefore,

Domain of R₁ = [–5, 5]

The range of R contains all the second elements of all the ordered pairs of R₁, i.e., y

It is also given y = 2x + 7

Now x ∈ [–5,5]

Multiply LHS and RHS by 2,

We get,

2x ∈ [–10, 10]

Adding LHS and RHS with 7,

We get,

2x + 7 ∈ [–3, 17]

Or, y ∈ [–3, 17]

So,

Range of R₁ = [–3, 17]

Q.8. If R₂ = {(x, y) | x and y are integers and x² + y² = 64} is a relation. Then find R₂.

Ans:

We have,

R₂ = {(x, y) | x and y are integers and x² + y² – 64}

So, we get,

x² = 0 and y² = 64 or x² = 64 and y² = 0

x = 0 and y = ±8 or x = ±8 and y = 0

Therefore, R₂ = {(0, 8), (0, –8), (8,0), (–8,0)}

Q.9. If R₃ = {(x, |x| ) |x is a real number} is a relation. Then find domain and range of R₃.

Ans:

According to the question,

R₃ = {(x, |x|) |x is a real number} is a relation

Domain of R₃ consists of all the first elements of all the ordered pairs of R₃, i.e., x,

It is also given that x is a real number,

So, Domain of R₃ = R

Range of R contains all the second elements of all the ordered pairs of R₃, i.e., |x|

It is also given that x is a real number,

So, |x| = |R|

⇒ |x|≥0,

i.e., |x| has all positive real numbers including 0

Hence,

Range of R₃ = [0, ∞)

Q.10: Assume that A = {1, 2, 3,…,14}. Define a relation R from A to A by R = {(x, y) : 3x – y = 0, such that x, y ∈ A}. Determine and write down its range, domain, and codomain.

Solution:

It is given that the relation R from A to A is given by R = {(x, y): 3x – y = 0, where x, y ∈ A}.

It means that R = {(x, y) : 3x = y, where x, y ∈ A}

Hence, R = {(1, 3), (2, 6), (3, 9), (4, 12)}

We know that the domain of R is defined as the set of all first elements of the ordered pairs in the given relation.

Hence, the domain of R = {1, 2, 3, 4}

To determine the codomain, we know that the entire set A is the codomain of the relation R.

Therefore, the codomain of R = A = {1, 2, 3,…,14}

As it is known that, the range of R is defined as the set of all second elements in the relation ordered pair.

Hence, the Range of R is given by = {3, 6, 9, 12}

Functions and Types of Functions

Functions

Function is a special type of relation.

Definition:-

A relation 'f' is said to be a function, if every element of a non-empty set X, has only one image or range to a non-empty set Y. Or. If 'f' is the function from X to Y and (x,y) ∊ f, then f(x) = y, where y is the image of x, under function f and x is the preimage of y, under 'f'.

Or

A relation ‘f’ is said to be a function, if every element of a non-empty set X, has only one image or range to a non-empty set Y.

Or

If ‘f’ is the function from X to Y and (x,y) ∊ f, then f(x) = y, where y is the image of x, under function f and x is the preimage of y, under ‘f’. It is denoted as;

f: X → Y.

Example: N be the set of Natural numbers and the relation R be defined as;

R = {(a,b) : b=a², a,b ∈ N}. State whether R is a relation function or not.

Solution: From the relation R = {(a,b) : b=a², a,b ∈ N}, we can see for every value of natural number, their is only one image. For example, if a=1 then b =1, if a=2 then b=4 and so on.

Therefore, R is a relation function here.

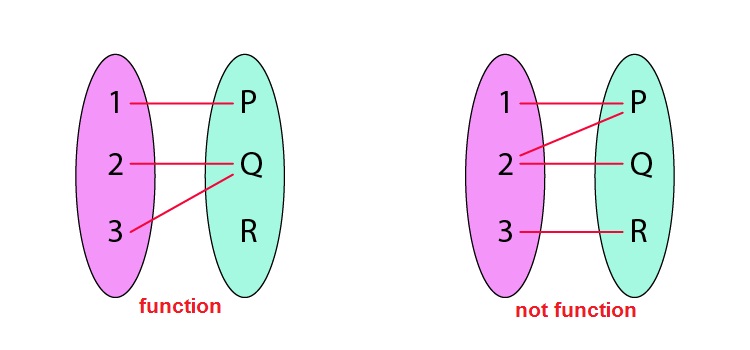
Types of Functions

There are various types of functions in mathematics which are explained below in detail. The different function types covered here are:

• One – one function (Injective function)
• Many – one function
• Onto – function (Surjective Function)
• Into – function
• Bijective – function
• Inverse -- function

One – one function (Injective function)

If each element in the domain of a function has a distinct image in the co-domain, the function is said to be one – one function.

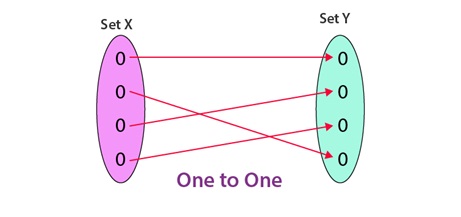
For examples f; R ->R given by f(x) = 3x + 5 is one – one.

Many – one function

On the other hand, if there are at least two elements in the domain whose images are same, the function is known as many to one.

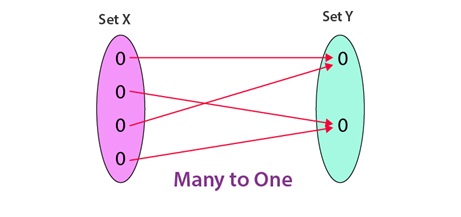
For example f : R-> R given by f(x) = x² + 1 is many one.

Onto – function (Surjective Function)

A function is called an onto function if each element in the co-domain has at least one pre – image in the domain.

Into – function

If there exists at least one element in the co-domain which is not an image of any element in the domain then the function will be Into function.

(Q) Let A = {x : 1 < x < 1} = B be a mapping f : A ->B, find the nature of the given function (f).

f(x) = |x|

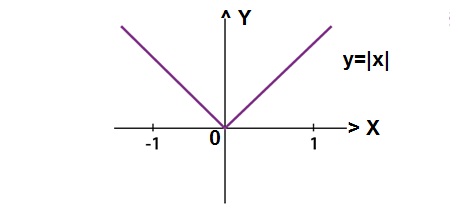
 f (x) = |1|

Solution for x = 1 & -1

Hence it is many one the Range of f(x) from [-1, 1] is

[0,1] which is not equal to co-domain. Hence it is into function.

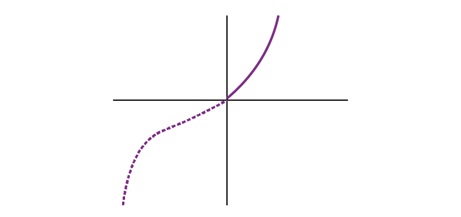
Lets say we have function,

f(x)={x²;x≥0−x²;x<0

For different values of Input, we have different output hence it is one – one function also it manage is equal to its co-domain hence it is onto also.

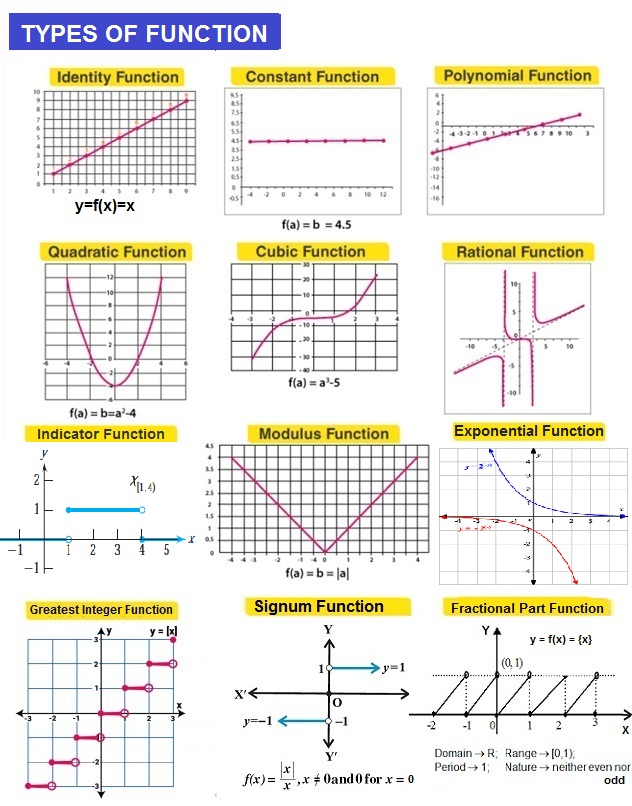
Special Types of Functions

• Constant Function
• Identity Function
• Polynomial function
• Linear Function
• Identical Function
• Quadratic Function
• Rational Function
• Algebraic Functions
• Cubic Function
• Modulus Function
• Signum Function
• Greatest Integer Function
• Smallest Integer Function
• Step Function
• Characteristics Function
• Indicator Function
• Fractional Part Function
• Exponential Function
• Logarithmic Function
•  Sinusoidal. Function
• Even and Odd Function
• Periodic Function
• Composite Function

Polynomial function

A real valued function f : P → P defined by y = f (a)=h₀+h₁ a+…..+h_n a_n, where n ϵ N, and h₀+h₁+…..+h_n ϵ P, for each a ϵ P, is called polynomial function.

• N = a Natural Number.
• The degree of Polynomial function is the highest power in the expression.
• If the degree is zero, it’s called a constant function.
• If the degree is one, it’s called a linear function. Example: b = a+1.
• Graph type: Always a straight line.

So, a polynomial function can be expressed as :

f(x)=a_nx_n+a_n−1x_n−1+…..+a₁x₁+a₀

The highest power in the expression is known as the degree of the polynomial function. The different types of polynomial functions based on the degree are:

1. The polynomial function is called a Constant function if the degree is zero.
2. The polynomial function is called a Linear if the degree is one.
3. The polynomial function is Quadratic if the degree is two.
4. The polynomial function is Cubic if the degree is three.

Linear Function

All functions in the form of ax + b where a, b∈R & a ≠ 0 are called as linear functions. The graph will be a straight line. In other words, a linear polynomial function is a first-degree polynomial where the input needs to be multiplied by m and added to c. It can be expressed by f(x) = mx + c.

For example, f(x) = 2x + 1 at x = 1

f(1) = 2.1 + 1 = 3

f(1) = 3

Another example of linear function is y = x + 3

Identical Function

Two functions f and g are said to be identical if

(a) The domain of f = domain of g

(b) The range of f = the Range of g

(c) f(x) = g(x)∀  x∈D_f & D_g

For example f(x) = x & g(x) =11/x

Solution: f(x) = x is defined for all x

But g(x) = 11/x is not defined of x = 0

Hence it is identical for x ∈R -{0}

Quadratic Function

All functions in the form of y = ax² + bx + c where a, b, c∈R, a ≠ 0 will be known as Quadratic function. The graph will be parabolic.

At x=−b±D2, we will get its maximum on minimum value depends on the leading coefficient and that value will be −D4a (where D = Discriminant)

In simpler terms,

A Quadratic polynomial function is a second degree polynomial and it can be expressed as;

F(x) = ax² + bx + c, and a is not equal to zero.

Where a, b, c are constant and x is a variable.

Example, f(x) = 2x² + x – 1 at x = 2

If x = 2, f(2) = 2.2² + 2 – 1 = 9

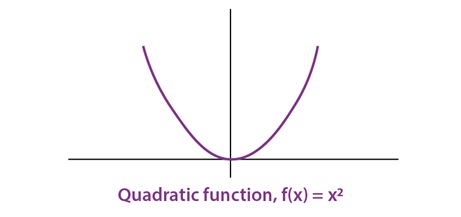
For Example: y = x² + 1

Read More: Quadratic Function Formula

Rational Function

These are the real functions of the type f(a)g(a) where f (a) and g (a) are polynomial functions of a defined in a domain, where g(a) ≠ 0.

• For example f : P – {– 6} → P defined by f (a) = f(a+1)g(a+2), ∀aϵP – {–6 }is a rational function.
• Graph type: Asymptotes (the curves touching the axes lines).

Algebraic Functions

A function that consists of a finite number of terms involving powers and roots of independent variable x and fundamental operations such as addition, subtraction, multiplication, and division is known as an algebraic equation.

For Example,

f(x)=5x3−2x2+3x+6, g(x)=3x+4(x−1)2.

Cubic Function

A cubic polynomial function is a polynomial of degree three and can be expressed as;

F(x) = ax³ + bx² + cx + d and a is not equal to zero.

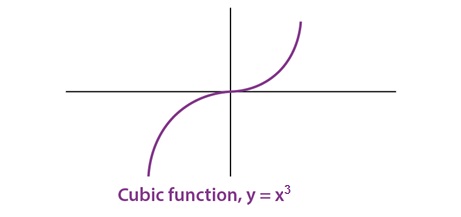
In other words, any function in the form of f(x) = ax³ + bx² + cx + d, where a, b, c, d∈R & a ≠ 0

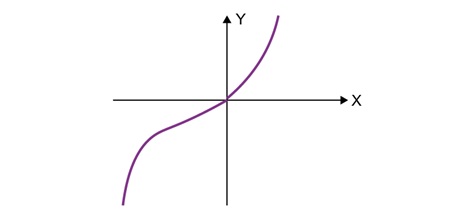
For example: y = x³

MODULUS FUNCTION:

A Function f(x) : R à R is said to be Modulus function if y=f(x) = |x| 

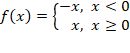
Domain of f = R

Range of f = R⁺U {0}

Codomain=R

 

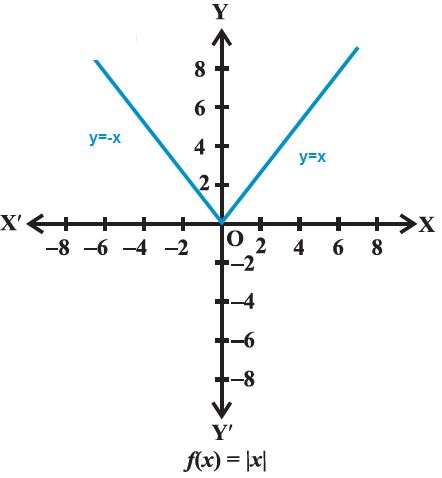
If x = -5, then y = f(x) = – (-5) = 5, since x is less than zero

If x = 10, then y = f(x) = 10, since x is greater than zero

If x = 0, then y = f(x) = 0, since x is equal to zero

When x = -3 then y = |-3| = 3

When x = -2 then y = |-2| = 2

When x = -1 then y = |-1| = 0

When x = 0 then y = |0| = 0

When x = 1 then y = |1| = 1

When x = 2 then y = |2| = 2

When x = 3 then y = |3| = 3

Signum Function:

A Function f(x) : R à R is said to be signum function if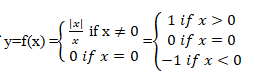  

Domain of f = R

Range of f = {-1,0,1}

Codomain=R

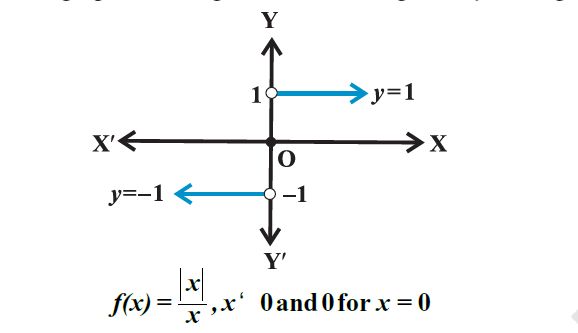
If x = -5, then y = f(x) = – 1 , since x is less than zero

If x = 5, then y = f(x) = 1 , since x is greater than zero

If x = 0, then y = f(x) = 0 , since x is equal to zero

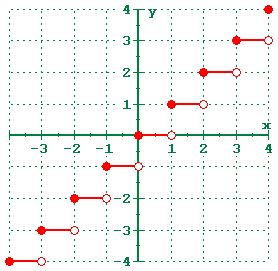
Greatest Integer Function:

A  Function f(x) : R à R is said to be greatest integer function if y=f(x)=[x]

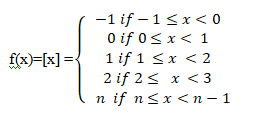
or

The function f: R , R defined by f(x) = [x], x R assumes the value of the greatest integer, less

than or equal to x. Such a function is called the greatest integer function.

Domain of f = R

Range of f = Z

Codomain=R

[1.15] = 1  , [1.9] =1

[4.56567] = 4  , [4.99] = 4

[50] = 50

[-3.010] = -4

Greatest Integer Function Properties

•  [x] = x, where x is an integer
• [x + n] = [x] + n, where n ∈ Z
• [-x] = –[x], if x ∈ Z
• [-x] =-[x] – 1, if x ∉ Z
• If [f(x)] ≥ Y, then f(x) ≥ Y

Smallest Integer Function:

Ceiling function f(x) = ⌈x⌉ and  floor function f(x)=⌊x ⌋

f(x) = ⌊x⌋ = Largest Nearest Integer of specified value

f(x) = ⌈x⌉ = Least Nearest successive Integer of specified value

A  Function f(x) : R à R is said to be Smallest integer function if y=f(x)= ⌊x ⌋

 

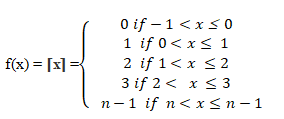
Domain of f = R

Range of f = Z

Codomain=R

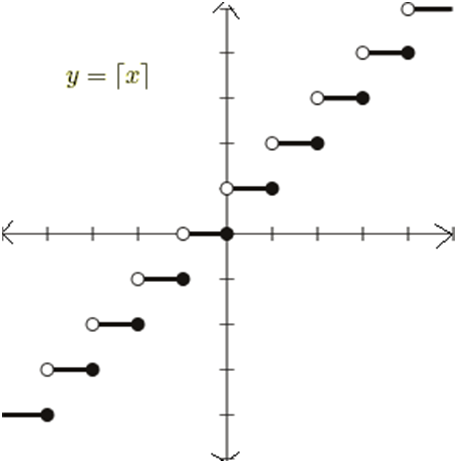
Properties:

• ⌈x⌉ + ⌈y⌉ – 1 ≤ ⌈x + y⌉ ≤ ⌈x⌉ + ⌈y⌉
• ⌈x + a⌉ = ⌈x⌉ + a
• ⌈x⌉ = a; iff x ≤ a < x + 1
• ⌈x⌉ = a; iff x – 1 < a ≤ x
• a < ⌈x⌉ iff a < x
• a ≤ ⌈x⌉ iff x < a

Step Function:

A step function (also called as staircase function) is defined as a piecewise constant function, that has only a finite number of pieces. In other words, a function on the real numbers can be described as a finite linear combination of indicator functions of given intervals.

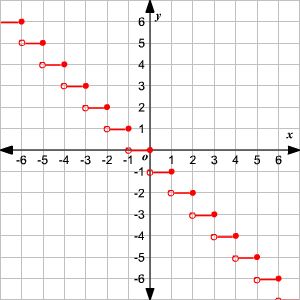
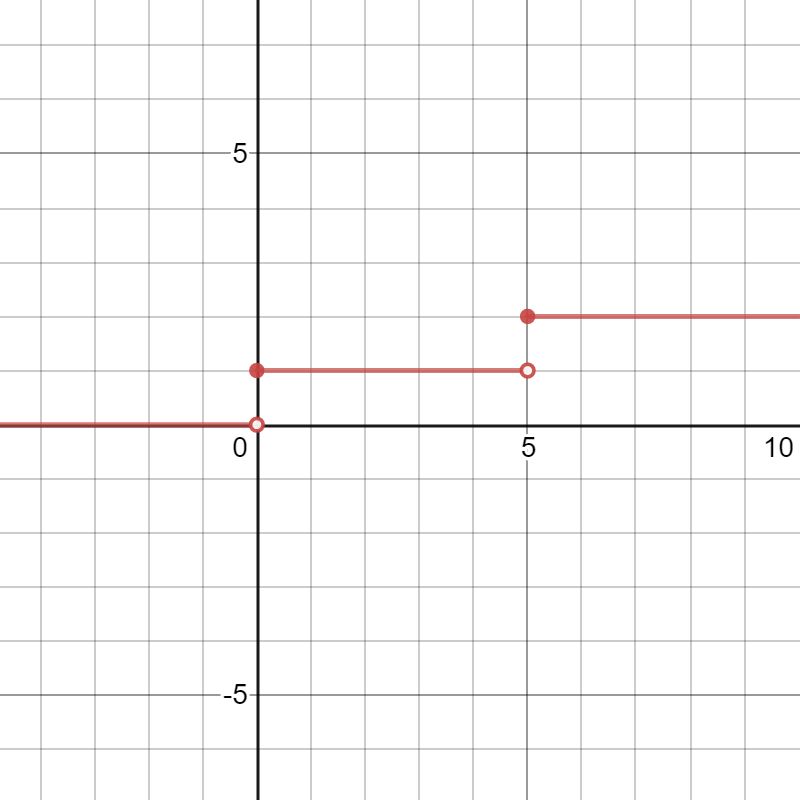
Domain of f = referred to as the set of input values

Range of f = referred to as the set of output values generated for the domain (input values)

Properties

The important properties of step functions are given below:

• The sum or product of two-step functions is also a step function.
• If a step function is multiplied by a number, then the result produced is again a step function. That indicates the step functions create an algebra over the real numbers
• A step function can take only a finite number of values
• Piecewise linear function is the definite integral of a step function

Indicator function / Characteristic function: 

An indicator function or a characteristic function of a subset of a set is a function that maps elements of the subset to one, and all other elements of the set to zero. The indicator function of a subset A of a set X maps X to the two-element set 

{ 0,1}; c_A(x)=1 if an element {displaystyle x}in X belongs to A

and c_A(x)=0 if x does not belong to A.

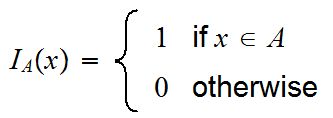
It may be denoted as 1_A , by I_A or by c_A

The indicator function of a subset, that is the function

c _A : X à {0,1}

which for a given subset A of X, has value 1 at points of A and 0 at points of X − A.

Fractional Part Function:

The fractional part function is the difference between a number and its integer part.

A  Function f(x) : R à R is said to be fractional part function if  y = f(x) = {x} = x- [x]

Domain of a fractional function is all the real numbers except the roots of denominator of the fraction.

Codomain =R

Range = [0,1)

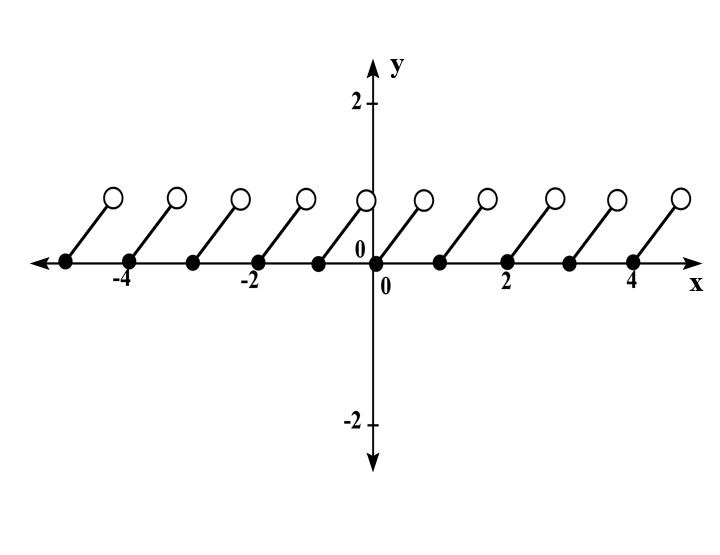
{1}=1−[1]=1-1=0.

Properties;

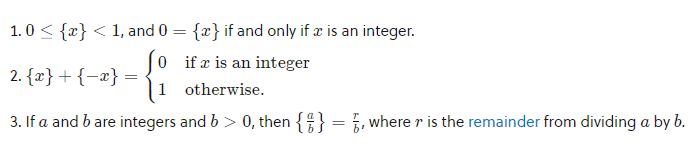
Exponential Function:

For a > 1, the Exponential of b to base a is x if y =f(x)=  a^x = b. Thus, The  function is known as Exponential function

Exponential function having base 10 is known as a common exponential function.

i.e.,y=f(x)= 10^x

Exponential function having base e is known as a Natural exponential function.

y=f(x)= e^x

Domain =R

Codomain =R⁺

Range = R⁺

Properties:

• The graph passes through the point (0,1).
• The domain is all real numbers
• The range is y>0
• The graph is increasing
• The graph is asymptotic to the x-axis as x approaches negative infinity
• The graph increases without bound as x approaches positive infinity
• The graph is continuous
• The graph is smooth

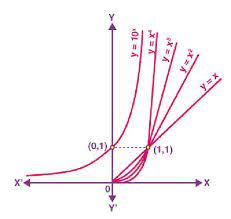
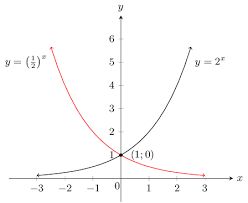
If a>0, and  b>0, the following hold true for all the real numbers x and y:

• • a^x a^y = a^x+y
  • a^x/a^y = a^x-y
  • (a^x)^y = a^xy
  • a^xb^x=(ab)^x
  • (a/b)^x= a^x/b^x
  • a⁰=1
  • a^-x= 1/ a^x

Logarithmic Function:

For a > 1, the logarithm of b to base a is x if a^x = b. Thus, log_a b = x if a^x = b. This function is known as logarithmic function.

logarithm function having base 10 is known as a common logarithm function.

i.e.,y=f(x)= log₁₀ x

logarithm function having base e is known as a Natural logarithm function.

y=f(x)= log_e x= lnx

Domain = R⁺

Codomain =R

Range = R

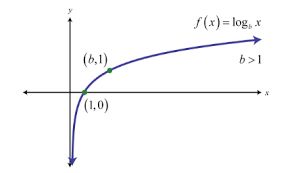
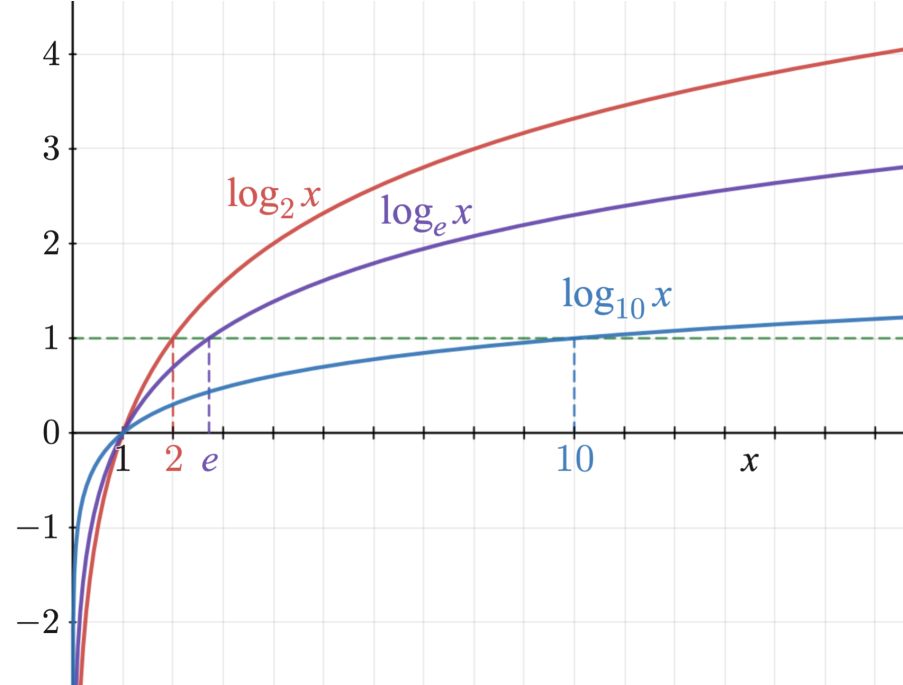
Properties:

• The graph passes through the point (1,0).
• The domain is all +ve real numbers
• Log_ap = α, log_bp = β and log_ba = µ, then a^α = p, b^β = p and b^µ = a
• Log_bpq = Log_bp + Log_bq
• Log_bp^y = ylog_bp
• Log_b (p/q) = log_bp – log_bq
• When we plot the graph of log functions and move from left to right, the functions show increasing behaviour.
• The graph of log function never cuts the x-axis or y-axis, though it seems to tend toward them.

Sinusoidal Function:

A sinusoidal function is a function using the sine function. The basic form of a sinusoidal function is  where A is the amplitude or height of our function, B is the change in period defined by   the horizontal shift, and D the vertical shift.​​​​​​​

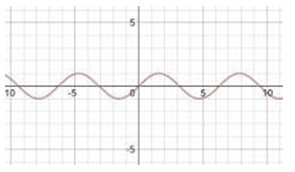
The sine and cosine functions have several distinct characteristics:

​​​​​​​

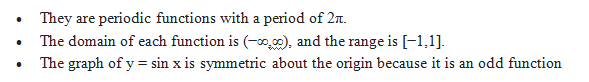
Even and Odd Function:

The definition of even and odd functions:

 Even function: A function, f(x) is even if f(x) = f(-x) 

Example:f(x)=cosx

 f(-x)=cos(-x)= cosx=f(x)

so f is even function.

examples of even functions are x⁴, cot x, y = x², etc.

Odd Function: A function, f(x) is odd if f(x) = -f(x) For example,

Check if function is even or odd: f (x) = tan x

f(-x)=tan(-x)= -tanx=-f(x)

so f is odd function.

The polynomial function f(x)=x2+x4+x6 is even. The polynomial function f(x)=x+x3+x5 is odd

Periodic Function:

A function y= f(x) is said to be a periodic function if there exists a positive real number P such that f(x + P) = f(x), for all x belongs to real numbers. The least value of the positive real number P is called the fundamental period of a function.

This fundamental period of a function is also called the period of the function, at which the function repeats itself. f(x + P) = f(x)

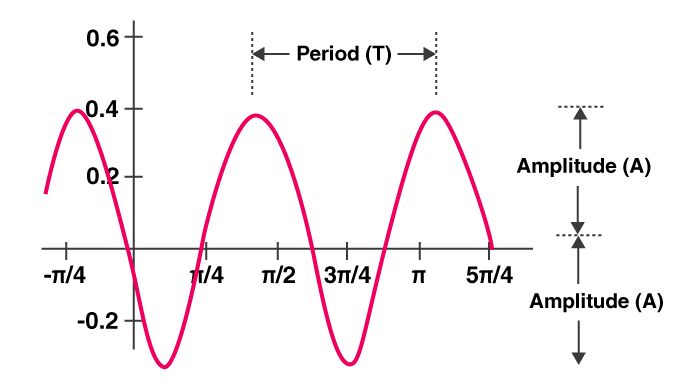
The period of the sine ,cosine function is 2π (units). All the trigonometric functions are periodic functions.

Composite Function:

Let f : A → B and g : B → C be two functions. Then the composition of f and g, denoted by g ∘ f, is defined as the function g ∘ f : A → C given by g ∘ f (x) = g(f (x)), ∀ x ∈ A.

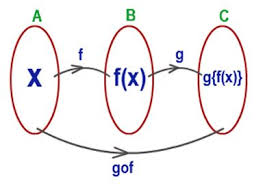
The composite function gof(x) is read as “g of f of x”. If f(x)and g(x) are two functions then fog(x), gof(x), gog(x) and fof(x) are composite functions.

• fog(x) = f(g(x))
• gof(x) = g(f(x))
• gog(x) = g(g(x))
• fof(x) = f(f(x))
• fogoh(x) = f(g(h(x)))
• fofof(x) = f(f(f(x)))

The order of the function is important in a composite function since (fog)(x) is not equal to (gof)(x).

 

Algebra of real functions

Examples:

Q.1: Write the range of a Signum function.

Solution:

The real function f: R → R defined by

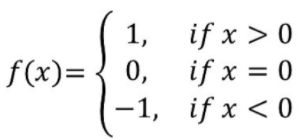
is called the signum function. Domain of f = R, Range of f = {1, 0, – 1}

Q.2: Express the function f: A—R. f(x) = x² – 1. where A = { -4, 0, 1, 4) as a set of ordered pairs.

Solution:

Given,

A = {-4, 0, 1, 4}

f(x) = x² – 1

f(-4) = (-4)² – 1 = 16 – 1=15

f(0) = (0)² – 1 = -1

f(1) = (1)² – 1 = 0

f(4) = (4)² – 1 = 16 – 1 =15

Therefore, the set of ordered pairs = {(-4, 15), (0, -1), (1, 0), (4, 15)}

Q.3: Let f(x) = x² and g(x) = 2x + 1 be two real functions. Find

(f + g) (x), (f –g) (x), (fg) (x), (f/g ) (x)

Solution:

Given,

f(x) = x² and g(x) = 2x + 1

(f + g) (x) = x² + 2x + 1

(f – g) (x) = x² -(2x + 1) = x² – 2x – 1

(fg) (x) = x²(2x + 1) = 2x³ + x²

(f/g) (x) = x²/(2x + 1), x ≠ -1/2

Q.4: Redefine the function: f(x) = |x – 1| – |x + 6|. Write its domain also.

Solution:

Given function is f(x) = |x – 1| – |x + 6|

Redefine of the function is:

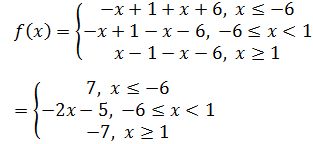
The domain of this function is R.

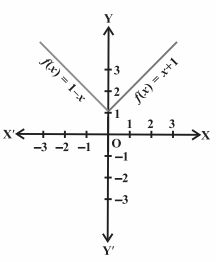
Q.5: The function f is defined by

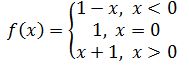
Draw the graph of f(x).

Solution:

f(x) = 1 – x, x < 0, this gives

f(– 4) = 1 – (– 4)= 5;

f(– 3) =1 – (– 3) = 4,

f(– 2) = 1 – (– 2)= 3

f(–1) = 1 – (–1) = 2; etc,

Also, f(1) = 2, f (2) = 3, f (3) = 4, f(4) = 5 and so on for f(x) = x + 1, x > 0.

Thus, the graph of f is as shown in the below figure.

Q.6: Find the domain and range of the real function f(x) = x/1+x².

Solution:

Given real function is f(x) = x/1+x².

1 + x² ≠ 0

x² ≠ -1

Domain : x ∈ R

Let f(x) = y

y = x/1+x²

⇒ x = y(1 + x²)

⇒ yx² – x + y = 0

This is quadratic equation with real roots.

(-1)² – 4(y)(y) ≥ 0

1 – 4y² ≥ 0

⇒ 4y² ≤ 1

⇒ y² ≤1/4

⇒ -½ ≤ y ≤ ½

⇒ -1/2 ≤ f(x) ≤ ½

Range = [-½, ½]