4. Trigonometric Equations

Trigonometric Equations:

Equations having trigonometric functions of a variable is known as Trigonometric Equations.

The equation is not completely solved unless we obtain an expression for all angles which satisfy it.

 Example: sin²x + 7 cos x – 7 = 0 ,

                  sin 3x + 3 cos²x = 7 , etc.

All trigonometric ratios are periodic in nature, a trigonometric equation has in general, an infinite no.  of solution.

So , the solutions of trigonometric equation may be categorized as:

Types of Solutions:

1. General solution
2. Principal solution

Principal Solution :

The solutions of these equations for a trigonometric function in variable x, where x lies in between 0≤x≤2π is called as principal solution.

General Solution:

If the solution contains the integer ‘n’ ,which gives all solution, it is called as the general solution.

Sometimes:

Particular Solution:

A Specific Value of x (the unknown angle) which satisfy the given equation.

N.B.: 1. The General Solution. contains Principal Solution as well as Particular solution

         2. Principal Solution always two

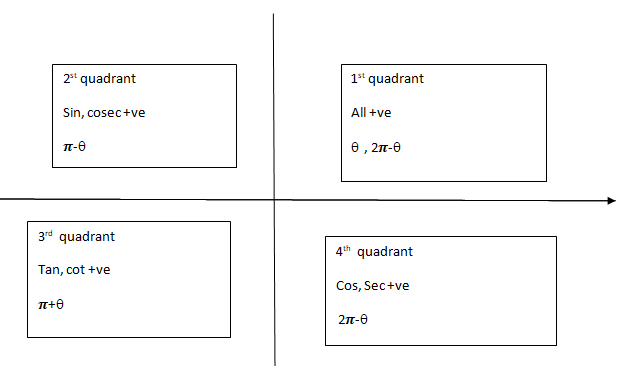
Table 

Proof :

 sin x = sin y implies x = nπ + (-1)ⁿ y , where n € Z and x and y are any real numbers.

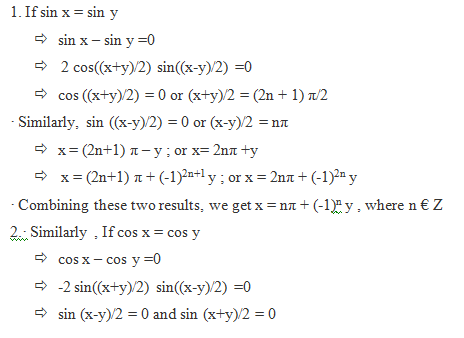
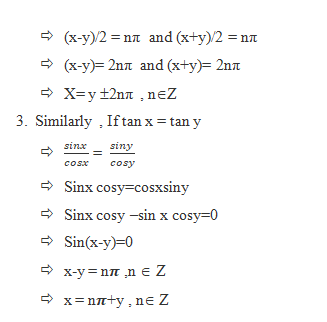
Q 1: If f(x) = tan 3x, g(x) = cot (x – 60) and h(x) = cos x,

find x given f(x) = g(x). Also, if h(x) = 4/5, find cosec x + tan³x.

Solution: If f(x) = g(x), so tan 3x = cot (x – 50)

=>cot (90 – 3x) = cot (x-50)

=> 90 – 3x = x – 50

or x = 35

For h(x)=cos x and h(x) = 4/5, we have cos x = 4/5.

Therefore, sin x = 3/5, cosec x = 5/3 and tan x = 4/5

Or, cosec x + tan³x = (5/3) + (4/5)³ = 817/375 = 2.178

Q 2: Find the principal solutions of the equation tan x = – 1/(√3).

Solution: We know, tan(π/6) = 1/(√3)

Since, tan (π – π/6 ) = -tan(π/6) = – 1/(√3)

Further, tan (2π – π/6) = -tan(π/6) = – 1/(√3)

Hence, the principal solutions are tan (π – π/6) = tan (5π/6) and tan (2π – π/6 ) = tan (11π/6)

Q 3: Evaluate the value of sin (11π/12).

Solution:

sin (11π/12) can be written as sin (2π/3 + π/4)

using formula, sin (x + y) = sin x cos y + cos x sin y

sin (11π/12) = sin (2π/3 + π/4) = sin(2π/3) cos (π/4) + cos(2π/3) sin (π/4)

= (√3)/2 x √2/2 + (-1/2) x √2/2

= √6/4 – (√2)/4

= (√6-√2)/4

Q 4: Evaluate cosec x = 2.

Solution: We know, cosec x = cosec π/6 = 2 or sin x = sin π/6 = 1/2 .

•  x = n π + (-1)ⁿ π/6

Q 5: Solve 5 cos²y + 2 sin y = 0.

Solution: 5 cos²y + 2 sin y = 0

•  5 (1 – sin² y) + 2 sin y = 0
•  5 sin²y – 2 sin y – 5 =0
• sin y = 1.2 or sin y = -0.8.

Since sin y can not be greater than 1,

sin y = – 0.8 = sin ( π + π/3 )

or, sin y = sin (4π/3) and hence, the solution is given by y = n π + (-1)ⁿ (4π/3)

Q 6: Find the principal solutions of the equation sin x = (√3/2)

Solution: Let y=sin^-1 (√3/2)

• sin y = (√3/2)
• sin y= sin( π/3)  and sin (2π/3) = sin (π – π/3 ) = sin π/3 = (√3/2)

Therefore, the principal solutions are x = π/3 and 2π/3.