2. Venn Diagrams and Operations on Sets

VENN-DIAGRAMS & OPERATIONS ON SETS

Venn-diagrams:

The graphical representation of a set is called Venn-diagram.

A Venn diagram is an illustration that uses circles to show the relationships among things or finite groups of things. Circles that overlap have a commonality while circles that do not overlap do not share those traits. Venn diagrams help to visually represent the similarities and differences between two concepts.

A diagram used to represent all possible relations of different sets. A Venn diagram can be represented by any closed figure, whether it be a Circle or a Polygon (square, hexagon, etc.). But usually, we use circles to represent each set. 

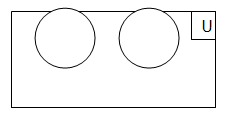
A large rectangle is used to represent the universal set and it is usually denoted by the symbol E or sometimes U.

All the other sets are represented by circles or closed figures within this larger rectangle.

Every set is the subset of the universal set U.

Operations on sets:

Union f sets:

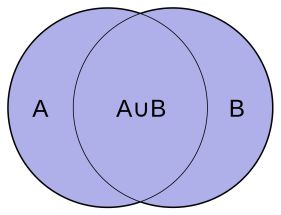
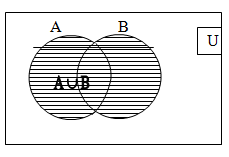
Let A and B be two sets, then the union of A & B is the set of all those elements which belong to A or to B or to both A and B. It is represented as AÈB.

  

Example: 

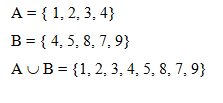
Properties:

(1) A È B = B È A           (Commutative law)                      

(2) A Í A È B & B Í A È B

(3) A È A = A (Idempotent law)

(4) A È f = A (Identity law)

(5) A È U = U where U is the universal set.

The union of n sets i.e. A₁, A₂, A₃ ……… A_n is denoted by

A₁ È A₂ È A₃ ---------- È A_n =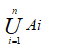

(6) AÍ B Þ AUCÍ BUC  then A Í AUC for any C

(7) AUB = B  iff  A Í B

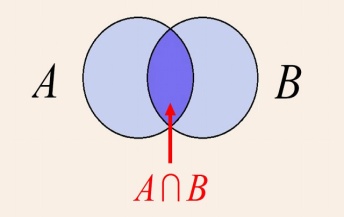
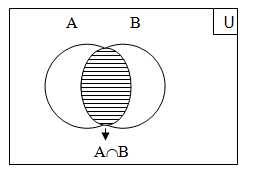
 Intersection of Two sets:

Let A & B are two sets. The intersection of A & B, denoted by A Ç B is a set of all elements those belongs to both A & B.

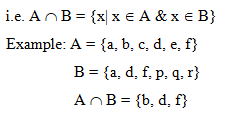
 Properties of Intersection:

 Facts:

 (1) A Ç B = B Ç A (Commutative law)

 (2) A Ç A = A (Idempotent law)

 (3) A Ç f = f (Identity law)

 (4) A Ç B Í A & A Ç B Í B

 (5) A Ç U = A

Distributive for intersection over union

A È (BÇ C) = (A È B) Ç (A È C)

Distributive property for union over

A Ç (B È C) = (A Ç B) È (A Ç C)

The intersection of n different sets is written by

A₁ Ç A ₂ Ç A₃ ------- Ç A_n =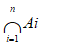 

Disjoint sets:

If the intersection of two sets A & B is a null set, then we say A & B are two disjoint sets.

Example:

A = {a, b, c}

B = {Rama, Shyama, Gopal}

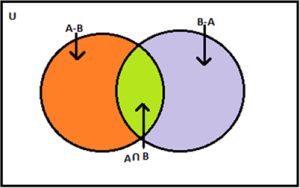
 Difference of sets:

Difference of sets:

The difference of two sets A & B, denoted by A – B, is the set of all element of A which do not belongs to B.  i.e.  A – B = {x| x Î A and x Ï B}

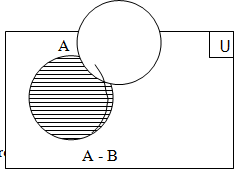
Example:

A = {1, 2, 3, 4, 5, 6}  B = {2, 5, 7, 11, 12, 13}

A – B = {1, 3, 4, 6}

 

Symmetric Difference of sets:

Let A and B are two sets. Then the symmetric difference of A & B, written by A D B is defined as

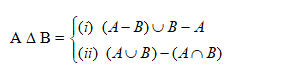
i.e. the set of all elements which are not common to both A & B.

Example: A = {1, 2, 3, 4, 5, 6, 7, 8},  B = {5, 7, 8, 10, 11, 12}

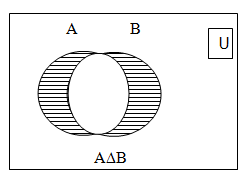
A D B = {1, 2, 3, 4, 6, 10, 11, 12}

Note:   A D B = B D A

 Complement of a set (w.r.t. universal set U)

Let U be the universal set & A be any set  st. A Ì C. Then the complement of A with respect to U, denoter by A^c (or A¹) or U –A, is defined as the set of all elements of U which donot belongs to A.

 

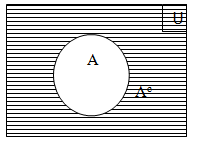
Example:

Z = { -----------  -3, -2, -1, 0, 1, 2, 3, ------------}  be the universal set.

A = { ----------  -4, -2, 0, 2, 4, --------------}

Then    A^c = { ------------   -3, -1, 1, 3, -------------}

Properties of complement:

Facts:

1. A Ç A^c = f
2. U^c = f & f^c = U
3. A È A^c = U
4. (A^c) = A
5. Demorgan’s laws

•  (i)  (AÈB)^| = A^| Ç B^|
•  (ii) (A Ç B)^| = A^| È B^|