- Books Name
- class 8 th Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 8
- Subject
- Mathmatics
Properties of polygon
Interior angle sum property of a quadrilateral
The sum of the measure of three angles of a triangle is 180°.
Proof:
Consider a triangle ABC with interior angles measures ∠1, ∠2 and ∠3.
Draw a line DE parallel to BC.
Now the angle formed by the parallel line DE with the triangle ABC is ∠4 and ∠5.
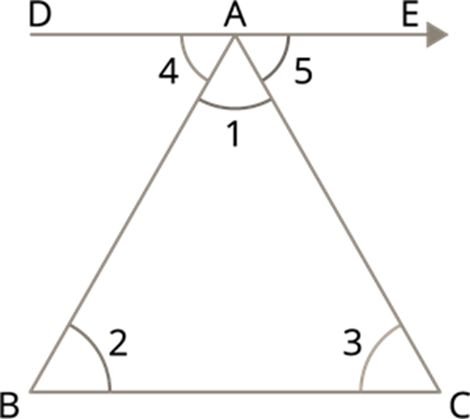
Since DE is parallel to BC, using the alternate interior angle property ∠2 must equal to ∠4. Similarly, ∠3 must be equal to ∠5.
That is ∠2=∠4 and ∠3=∠5. As DE is a straight line, ∠5 and ∠CAD are linear pairs (Pair of adjacent supplementary angles).
∠5+∠CAD=180° .
That is, ∠5+∠1+∠4=180°.
Equivalently, ∠1+∠2+∠3=180°.
It states that the total measures of the three angles of a triangle is 180°.
Interior angle sum property of polygons
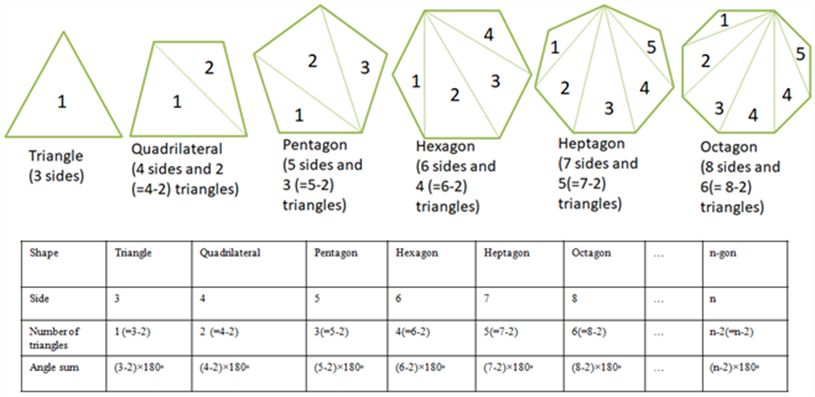
Exterior angle property of the polygons
If the side of a polygon is extended, the angle formed outside the polygon is the exterior angle.
The sum of all the exterior angles of a polygon is 360°.
Geometrical approach:
When all of the angles of a convex polygon converge or pushed together, they form one angle called one complete turn (Perigon angle), which measures 360 degrees.
If the sides of the convex polygon are increased or decreased, the sum of all of the exterior angles is still 360 degrees. More sides can be added to the polygon and they will still form 360°.
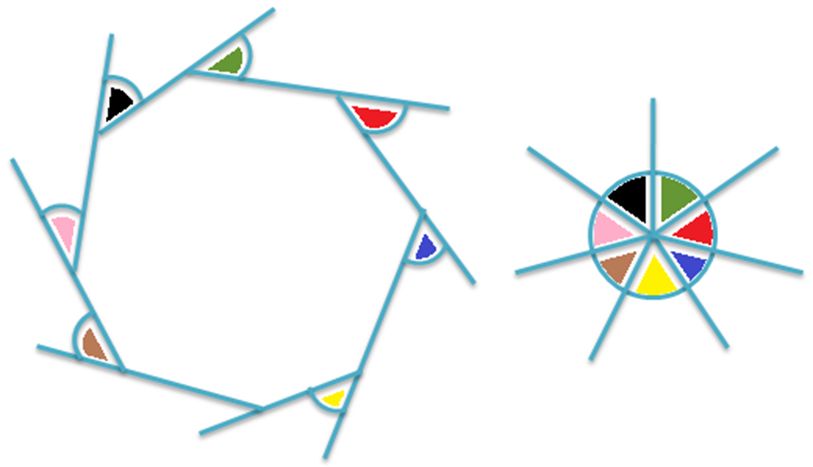
Therefore, the number of sides does not change the sum of the exterior angles of a convex polygon
Algebraic approach:
For any polygon, exterior angle + interior adjacent angle =180°
So, if the polygon has n sides, then:
Sum of all exterior angles + Sum of all interior angles =n×180°
So, the sum of all exterior angles =n×180° − Sum of all interior angles
Sum of all exterior angles =n×180°−(n−2)×180°
= n×180° −n×180° +2×180°
= 180°n −180°n +360°
=360°
Therefore, we conclude that the sum of all the exterior angles of the polygon having n sides = 360°.
- The sum of measures of all the exterior angles of a polygon is 360°.
- Each exterior angle of a regular polygon is 360°n, where n is the number of sides.
- The number of sides of a regular polygon n=360°eachexteriorangle.
- The sum of all the exterior angles formed by producing the sides of a convex polygon in the same order is equal to four right angles (4×90°=360°).

 ReginaTagebücher
ReginaTagebücher
