- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
Exterior Angle Property of a Triangle -
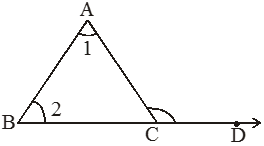

Illustration 1
Is it possible to draw a triangle whose sides are 3 cm, 4 cm and 7 cm ?
Solution
Sides of a triangle are 3 cm, 4cm, 7 cm.
Here 3 + 4 = 7
and we know that sum of two sides of a triangles is always greater than the third side so it is not possible to draw a triangle whose sides are 3 cm, 4 cm and 7 cm.
Illustration 2
In each of the following there are three positive numbers. State if these numbers could possibly be the lengths of the sides of a triangle.
(i) 2, 3, 4 (ii) 2.5, 1.5, 4
Solution
(i) We have,
2 + 3 > 4, 2 + 4 > 3 and 3 + 4 > 2
That is, the sum of any two of the given numbers is greater than the third number.
So, 2 cm, 3 cm and 4 cm can be the lengths of the sides of a triangle.
(ii) We have,
2.5 + 1.5 ≯ 4.
So, the given numbers cannot be the lengths of the sides of a triangle.
Illustration 3
The length of two sides of a triangle are 12 cm and 15 cm. Between what two measure should the length of the third side fall ?
Solution
Let x cm be the length of the third side.
Then 12 + x > 15; 15 + x > 12 and 12 + 15 > x.
⇒ x > 15 – 12; x > 12 –15 and 27 > x.
⇒ x > 3 ; x > – 3 and 27 > x.
A number greater than 3 is obviously greater than – 3.
∴ x > 3 and 27 > x.
Hence, x lies between 3 cm and 27 cm.
Property : Angles opposite to equal sides of a triangle are equal.
Property : Sides opposite to equal angles of a triangle are equal.
Property : In a right triangle, if a, b are the lengths of the sides and c that of the hypotenuse, then c2 = a2 + b2.
(Hypotenuse)2 = (Base)2 + (Perpendicular)2
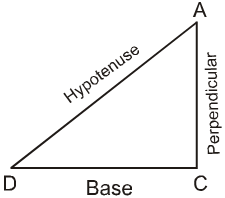
Property : If the sides of a triangle are of lengths a, b and c such that c2 = a2 + b2, then the triangle is right angled and the side of length c is the hypotenuse.
Note : Three positive numbers a, b, c in this order are said to form a pythagorean triplet, if
c2 = a2 + b2. Triplets (3, 4, 5) (5, 12, 13), (8, 15, 17), (7, 24, 25) and (12, 35, 37) are some pythagorean triplets.
Illustration 1
The sides of certain triangles are given below. Determine which of them are right triangles :
(i) a = 6 cm, b = 8 cm and c = 10 cm
(ii) a = 5 cm, b = 8 cm and c = 11 cm.
Solution
(i) Here the larger side is c = 10 cm.
We have : a2 + b2 = 62 + 82 = 36 + 64 = 100 = c2.
So, the triangle with the given sides is a right triangle.
(ii) Here, the larger side is c = 11 cm
Clearly, a2 + b2 = 25 + 64 = 89 ≠ c2.
So, the triangle with the given sides is not a right triangle.
Illustration 2
A ladder 25 m long reaches a window of a building 20 m above the ground. Determine the distance of the foot of the ladder from the building.
Solution
Suppose that AB is the ladder, B is the window and CB is the building. Then, triangle ABC is a right triangle, with right angle at C. 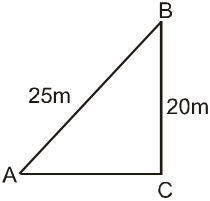
∴ AB2 = AC2 + BC2
⇒ 252 = AC2 + 202
⇒ AC2 = 625 – 400 = 225
![]()
Illustration 3
A ladder 17 m long reaches a window which is 8 m above the ground on one side of the street. Keeping its foot at the same point, the ladder is turned to the other side of the street to reach a window at a height of 15 m. Find the width of the street.
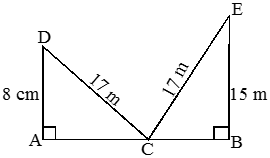
Solution
Let AB be the street and C be the foot of the ladder. Let D and E be the windows at the height of 8 m and 15m respectively from the ground.
Then, CD and CE are the two positions of the ladder.
In right triangle, DDAC, we have
AC2 + AD2 = CD2
⇒ AC2 = (CD2 – AD2)
= {(17)2 – (8)2} m2 = 289 – 64 = 225 m2
![]()
In right triangle, DCBE, we have
CB2 + BE2 = CE2
⇒ CB2 = (CE2 – BE2) = {(17)2 – (15)2} m2 = 64 m2
![]()
Hence, width of the street = AB = (AC + CB) = (15 + 8) m = 23 m.
Illustration 4
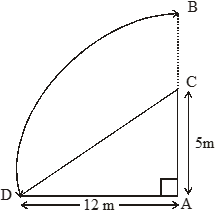
A tree has broken at a height of 5 m from the ground and its top touches the ground at a distance of 12m from the base of the tree. Find the original height of tree.
Solution
Let AB be the tree and Let C be the point at which it broke.
Then CB takes the position CD.
Original height of tree i.e., AB
i.e. AC + BC⇒ AC + CD (∵
i.e. ∆ACD, using pythagoras theorm, we
CD2 = AC2 + AD2
CD2 = (5)2 + (12)2 = 25 + 144 = 169
CD2 = 132
CD = 13 m
So. height of tree = AC + BC
= AC + CD
= (5+13) m
= 18 m
Hence, height of the tree = 18 m.

 ReginaTagebücher
ReginaTagebücher
 Param Publication
Param Publication
