- Books Name
- Class 6 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 6
- Subject
- Mathmatics
Chapter -5
Understanding Elementary Shapes
Line Segments, Angles and Triangles
Measuring a line,
LINES AND ANGLES
Babilonians used geometry during the period 3000 BC to 2000 BC. They found formulae for areas and perimeters of rectangle and square. To mark the boundaries of the fields that were affected by the floods due to the over flow of river Nile and to compute their areas, geometry came to help of Egyptians. From ancient Vedic times geometry got special importance in our country. Geometry was developed as a science along with astronomy in our country. ‘Kalpa’ is a part of vedas. Later on, geometry was developed as ‘sulbha sutras’. Great people like Boudhayana, Apasthambha, Katyana etc., became famous authors of such ‘sulbha sutras’.
Basic Geometrical Concepts
Axioms: The basic facts which are taken for granted without proof are called axioms.
E.g.:
Halves of equals are equal
The whole is greater than each of its parts
A line contains infinitely many points
Statements: A sentence which can be judged to be true or false is called a statement.
E.g.:
The sum of the angles of a triangle is 1800 is a true statement
x + 8 > 12 is a sentence but not a statement
Theorems: A statement that requires a proof is called a theorem. Establishing the truth of a theorem is known as proving the theorem.
E.g.:
The sum of the angles of a triangle is 180°.
Corollary: A statement, whose truth can easily be deducted from a theorem, is called its corollary.
Fundamental Geometrical Terms
Point: A point is a mark of position. A fine dot represents a point. We denote a point by a capital letter A, B, P, Q etc. A point has no length, breadth or thickness.
Line Segment: The straight path between two points A and B is the line segment AB, represented as ABAB.
The points A and B are called its end points.
A line segment has a definite length.

The distance between two points A and B gives the length of the line segment ABAB.
Ray: A line segment AB when extended indefinitely in one direction is the ray AB−→−AB→.
It has one end point A.

A ray has no definite length. A ray cannot be drawn; it can simply be represented on the plane of a paper.
Line: A line segment AB when extended indefinitely in both the directions is called line AB←→AB↔.

A line has no end points. A line has no definite length. A line cannot be drawn; it can simply be represented on the plane of a paper.
Incidence Axioms on Lines
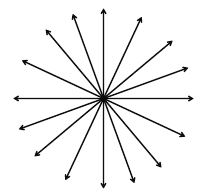
A line contains infinitely many points
An infinite number of lines can be drawn to pass through a given point
One and only one line can be drawn to pass through two given points A and B.

Collinear Points: Three or more points are said to be collinear, if there is a line which contains them all.
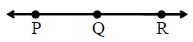
In the above figure; P, Q, R are collinear points.
Plane: A flat surface extended endlessly in all the four directions is called a plane. The surface of a smooth wall, the surface of the top of the table, the surface of a smooth blackboard, the surface of a sheet of paper etc. are close examples of a plane. These surfaces are limited in extent but the geometrical plane extends endlessly in all directions. Two lines lying in a plane either intersect exactly at one point or are parallel.
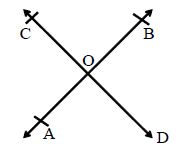
Intersecting Lines: Two lines having a common point are called intersecting lines. The point common to two given lines is called their point of intersection. In the figure, the lines AB and CD intersect at a point O.
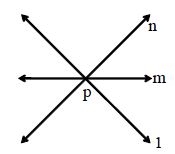
Concurrent Lines: Three or more lines in a plane are said to be concurrent, if all of them intersect at the same point. In the figure below, the lines l, m, n all intersect at the same point P; so they are concurrent.
Parallel Lines: Two lines l and m in a plane are said to be parallel, if they have no point in common and is written as l || m. The distance between two parallel lines always remains the same.

Angle and its Angle Types,
Angles: Two rays OA and OB having a common end point O form angle AOB, written as ∠∠AOB.
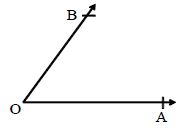
OA and OB are called the arms of the angle and O is called as its vertex.
Measure of an Angle: The amount of turning from OA to OB is called the measure of ∠∠AOB is written as ∠∠ AOB. An angle is measured in degrees, denoted by.
A complete rotation around a point makes an angle of 360°.
1° = 60 minutes, written as 60′.
1′ = 60 seconds, written as 60″.
We use a protractor to measure an angle.
Kinds of Angles
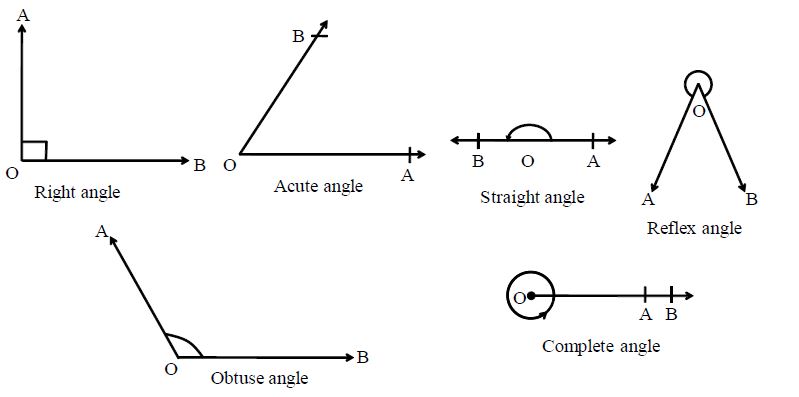
Right Angle: An angle whose measure is 90° is called a right angle.
Acute Angle: An angle, whose measure is more than 0° but less than 90°, is called an angle.
Obtuse Angle: An angle whose measure is more than 90° but less than 180° is called an obtuse angle.
Straight Angle: An angle whose measure is 180° is called a straight angle.
Reflex Angle: An angle whose measure is more than 180° but less than 360° is called a reflex angle.
Complete Angle: An angle whose measure is 360° is called a complete Angle.
Equal Angles: Two angles are said to be equal, if they have the same measure.
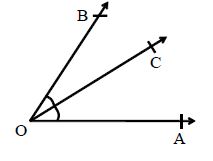
Bisector of an Angle: A ray OC is called the bisector of ∠∠AOB, if m ∠∠AOC= m ∠∠BOC.
Complementary Angles: Two angles are said to be complementary, if the sum of their measures is 90°.
Two complementary angles are called the complement of each other.
Thus, Complement of an angle of 36° = An angle of (90° – 36°) = 54°.
Supplementary Angles: Two angles are said to be supplementary, if the sum of their measures is 180°. Two supplementary angles are called the supplement of each other.
Thus, supplement of an angle of 42° = An angle of (180° – 42°) = 138°.
Supplement of an angle of 115° = an angle of (180° – 115°) = 65°.
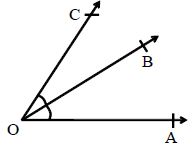
Adjacent Angles: Two angles are said to be adjacent angles, if they have a common vertex and a common arm such that the other arms of the two angles are on either side of their common arm.
In the adjoining figure, ∠∠AOB and ∠∠BOC are adjacent angles.
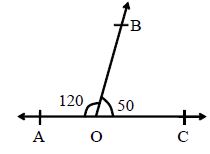
Linear Pair: If the sum of two adjacent angles is 180°, they are said to form a linear pair. In the adjoining figure, ∠∠AOB + ∠∠COB =.
So AOB and BOC together form a linear pair.
Important Results
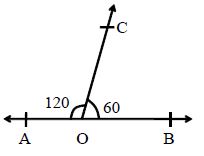
Linear Pair Axiom: If a ray stands on a straight line, then the sum of the adjacent angles so formed is 180°. Thus, ∠∠AOC + ∠∠COB = 180° where AOB is a straight line.
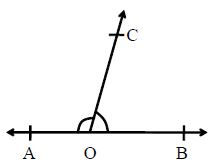
Converse of a Linear Pair Axiom: If two adjacent angles are supplementary, then the non-common arms of two angles are in a straight line. Thus if two adjacent angles ∠∠AOC and ∠∠BOC with common arm OB are such that ∠∠ AOC + ∠∠BOC = 180° then OA and OB are in the same straight line i.e. AOB is a straight line.
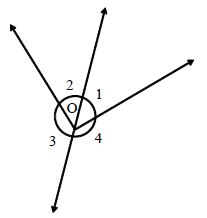
Angles at a Point: The sum of all the angles at a point is 360°.
In the given figure, we have ∠1 + ∠2 + ∠3 + ∠4 = 360°.
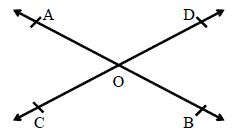
Vertically Opposite Angles: If two straight lines AB and CD intersect at a point O, then ∠AOC and ∠BOD form one pair of vertically opposite angles and the angles AOD and BOC form another pair of vertically opposite angles. When two lines intersect each other, then vertically opposite angles are always equal. In the given figure, we have: ∠AOC = ∠BOD and ∠BOC = ∠AOD.
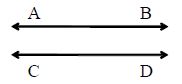
Parallel Lines: Two straight lines lying in the same plane are said to be parallel if they do not intersect no matter how long they are produced on either side. In the given figure, AB and CD are parallel lines and we write AB || CD.
Transversal: A straight line that intersects two or more lines is called a transversal. Let two lines AB and CD are cut by a transversal l, and then the following angles are formed.
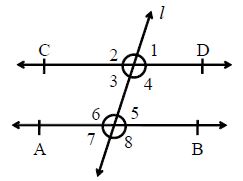
Pairs of Corresponding Angles (abbreviated as cores angel s): (angle 1, angle 5), (angle 2, angle 6), (angle 4, angle8), (angle 3, angle 7)
Pairs of Alternate Interior Angles (abbreviated as Alt. Int. angels): (angle 3, angle 5) and (angle 4, angle 6)
Pairs of Alternate Exterior Angles: (angle 2, angle 8) and (angle 1, angle 7)
Pairs of Consecutive Interior Angles (abbreviated as co. Int. s): (angle 4, angle 5) and (angle 3, angle 6)
Properties of Angles Associated with Parallel Lines
If two parallel straight lines are intersected by a transversal, then
Corresponding angles are equal. Angle 1 = angle 5, angle 2 = angle 6, angle 4 = angle 8 and angle 3 = angle 7
Alternate interior angles are equal. Angle 3 = angle 5 and angle 4 = angle 6
Alternate exterior angles are equal. Angle 2 = angle 8 and angle1 = angle 7
Co-interior angles (consecutive interiors) are supplementary. Angle 4 + angle 5 = 180° and angle 3 + angle 6 =180°.
Conditions of Parallelism: The converse of the above results is also true.
If two straight lines are intersected by transversal such that pair of corresponding angles is equal, then the two lines are parallel.
If two straight lines are intersected by a transversal such that pair of alternate angles is equal, then the two lines are parallel.
If two straight lines are intersected by a transversal such that a pair of consecutive interior angles is supplementary, then the two lines are parallel.
Basic Axiom of Parallel Lines: (Euclidian postulate)
There exists one and only one line which is parallel to a given line from a given point.
If two lines are parallel to the same line then the lines are parallel to each other.
TRIANGLE
A closed plane figure bounded by three line segments is called a Triangle. We denote a triangle by the symbol Δ∆. Δ∆ABC has:
Three vertices, namely A, B and C
Three sides, namely AB, BC and CA
Three angles, namely, ∠A, ∠B and ∠C.
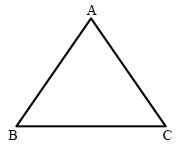
The three sides and the three angles are known as elements or parts of the Triangle.
Kinds of Triangles
Classification of Triangles according to Sides:
Scalene Triangle: A triangle, in which all sides are of different lengths, is called a scalene triangle.
In the following figure, ΔPQR∆PQR is a scalene triangle
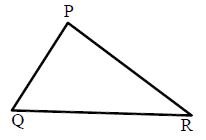
since PQ≠QR≠PRPQ≠QR≠PR
Isosceles Triangle: In an isosceles triangle, the angles opposite to the equal sides are equal. A triangle having two sides equal is called an isosceles triangle.
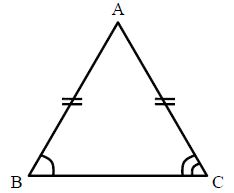
In ΔABC; AB=AC⇒∠B=∠CΔABC; AB=AC⇒∠B=∠C.
Equilateral Triangle: A triangle which is having equal sides is called an equilateral triangle. The measure of each angle of an equilateral triangle is 60°.
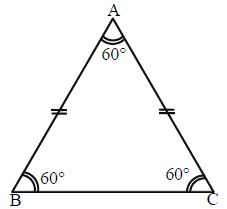
Classification of Triangles according to Angles:
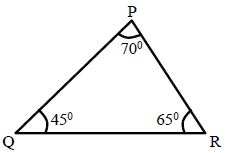
Acute-Angled Triangle: A triangle, in which every angle measures more than 0° but less than 90°, is called an acute-angled triangle. In the below figure Δ∆PQR, we have: ∠P = 70°, Q = 45° and R = 65°.
Thus, each angle of PQR is acute.
Right-Angled Triangle: A triangle in which one of the angles measures 90° is called a right angled triangle or simply a right triangle. In a right-angled triangle the side opposite to the right angle is called its hypotenuse and the remaining two sides are called its legs.
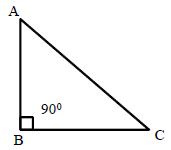
Δ∆ABC is a right triangle and ∠B = 90°, AC is the hypotenuse and AB and BC are its legs.
Obtuse-Angled Triangle: A triangle in which one of the angles measures more than 90° but less than 180° is called an obtuse- angled triangle.
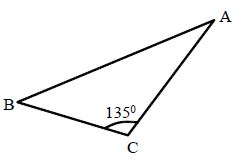
Here, Δ∆ABC is an obtuse-angled triangle in which ∠C =135°.
Median: A line segment joining a vertex to the mid-point of the opposite side of a triangle is called a median of the triangle. In the below figure, D is the mid-point of side BC of ABC. AD is a median of ABC. A triangle has 3 medians.
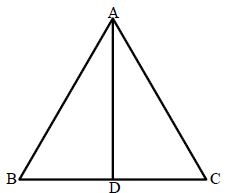
All the three medians of a triangle are concurrent i.e. they intersect at a point
Centroid: The point of intersection (concurrence) of the three medians of a triangle is called its centroid.
In the below figure, the three medians AD, BE and CF intersect at the point G.
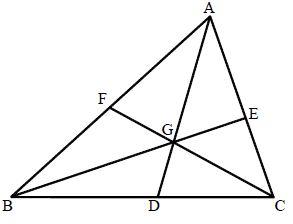
G is the centroid of Δ∆ABC
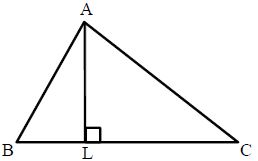
Altitude: The length of perpendicular from a vertex to the opposite side of a triangle is called its altitude and the side on which the perpendicular is being drawn, is called its base. In the below figure, AL⊥⊥BC.
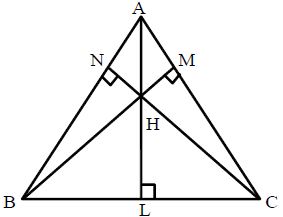
So BC is the base and AL is the corresponding altitude of the triangle. A triangle has three altitudes. All the three altitudes of a triangle are concurrent i.e., they intersect at a point.
Orthocentre: The point of intersection (concurrence) of the three altitudes of a triangle is called its orthocentre. In the figure below, the three altitudes AL, BM and CN of Δ∆ABC intersect at a point H.
Therefore, H is the orthocentre of ABC.
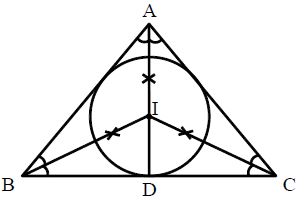
In centre and in circle: The point of intersection of the internal bisectors of the angles of a triangle is called its in centre in the below figure, the bisectors of the internal angles of a Δ∆ABC meet at a point I. So, ‘I’ is the in centre of ABC. The in centre of a triangle is the center of a circle which touches all the sides of the triangle and this circle is called the in circle of the triangle. If ID⊥⊥BC, then ID is called the radius of the in circle.
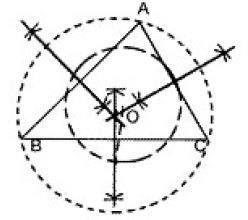
Circumcentre and Circumcircle: The point of intersection of the perpendicular bisectors of the sides of a triangle is called its circumcentre. In the below figure, the perpendicular bisectors of the sides AB, BC and CA of Δ∆ABC intersect at a point O. So O is the Circumcentre of the triangle. The circumcentre of a triangle is the centre of a circle which passes through the vertices of the triangle and this circle is called the circumcircle of the triangle. Clearly, OA = OB = OC = radius of circumcircle.
Exterior and Interior Opposite Angles of a Triangle: Take a triangle ABC whose one side BC will make to D; then an exterior angle is triangle ACD. and its interior opposite angles is the angles A and B .
Properties of Triangles
Angle Sum Property: The angles of a triangle have the sum of 180°.
When the two sides of a triangle are equal in length, then the opposite angles to them are of equal measures.
In a triangle, the sum of angles of any two sides is always greater than the angles of third side.
Whenever the 2 sides of a triangle are of not equal length, then the greater side of the triangle has the greater angle of triangle opposite to it.
If any one side of a triangle is making the exterior angle then it is equal to sum of all other interior opposite angles.
In a triangle the outer angle is always, greater than its inner opposite angle. The sum of (outer) exterior angles of a triangle is always 360°.

 Param Publication
Param Publication
 ReginaTagebücher
ReginaTagebücher
