1. Direction cosines and direction ratios of a line joining two points.
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Chapter 11
Three-Dimensional Geometry
Direction Cosines
In three-dimensional geometry, we have three axes: namely, the x, y, and z-axis. Let us assume a line OP passes through the origin in the three-dimensional space. Then, the line will make an angle each with the x-axis, y-axis, and z-axis respectively.
The cosines of each of these angles that the line makes with the x-axis, y-axis, and z-axis respectively are called direction cosines of the line in three-dimensional geometry. Normally, it is tradition to denote these direction cosines using the letters l, m, n respectively.
Note that these cosines can be found only once we have found the angles that the line makes with each of the axes. Also, it is interesting to note that if we reverse the direction of this line, the angles will obviously change.
Consequently, the direction cosines i.e. the cosines of these angles will also be different once the direction of the line is reversed. We will now look at a slightly different situation where our line does not pass through the origin (0,0,0).
1.Direction cosines and direction ratios of a line joining two points:
Let a line AB in 3D space make angles α, β, γ respectively with the +ve direction of coordinate axes X, Y, Z. Therefore, we express cosα, cosβ, cosγ as direction cosines of the line AB in the 3D space. Clearly; direction cosines fix the direction cosines of a line in space. Also, parallel lines have the same direction cosines. Direction cosines are denoted by l, m, n respectively. i.e. l = cosα, m = cosβ and n = cosγ. The direction of a line cannot be fixed in space by knowing anyone or any two angles.
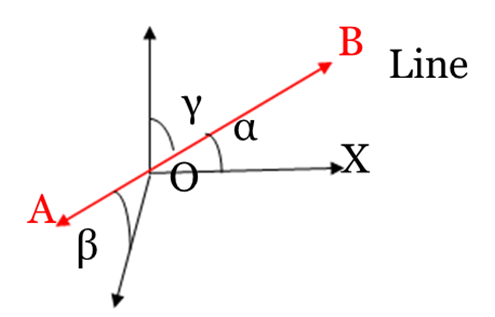
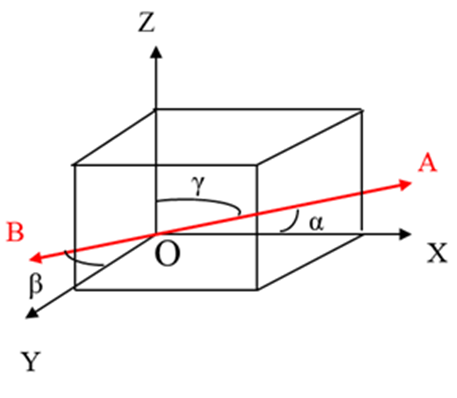
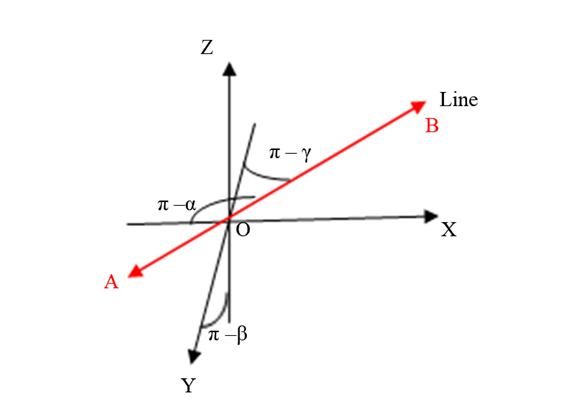
If a line in space makes angles α, β, γ respectively with the +ve direction of X, Y, Z axes then we can assume that the line will make angles π – α, π – β, π – γ with the -ve direction of axes. Therefore, the direction cosines can also be written as cos π -α, cos π -β, cos π –γ. Thus, direction cosines of the same line may also be taken as – cosα, –cosβ, –cosγ.
Three numbers a, b, c proportional to direction cosine l, m, n of a line in space. These numbers are called direction ratios OR direction numbers of the line. Therefore, the direction cosines of a line will be fixed but not the direction ratios:
![]()
Let direction cosine of any line in space be l, m, n and direction ratios(d.r.’s) are a:b:c.
Let P(x,y,z) be any point on the line and PM is perpendicular from P on X-axis. Then, in right triangle PMO,
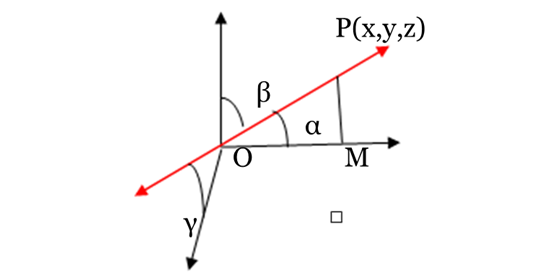
We can see that cosα=OMOP=x/r . In this case x = OM and r = OP or l=x/r
Similarly, we take the perpendicular point P on y and axis to obtain: m=y/r ; n=z/r
Hence, we conclude that
r2=x2+y2+z2=(lr)2+(mr)2+(nr)2
- r2=[l2+m2+n2] r2
- l2+m2+n2=1

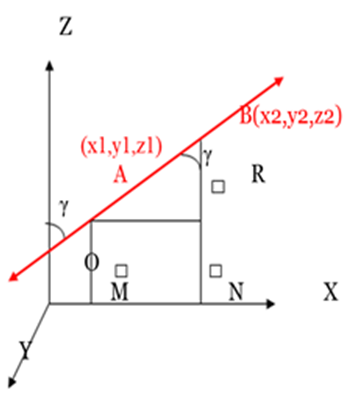
Let AB be a line that is inclined at angles α, β, γ with positive x, y, z-axis at points A (x1, y1, z1) and B at (x2, y2, z2) to form direction ratios. Line AB makes angle γ with the z-axis which is a part of a right angle triangle ∆ARB where,
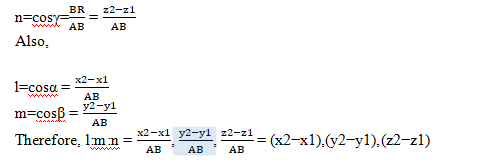
Solved Examples
Example : Find the direction ratios and direction cosines of a line joining the points (3, -4, 6) and (5, 2, 5).
Solution:
Given points are A(3, -4, 6) and B(5, 2, 5)
The direction ratios of the line joining AB is
a = x2 – x1 = 5 – 3 = 2
b = y2 – y1 = 2 + 4 = 6
c = z2 – z1 = 5 – 6 = -1
AB =
So direction cosines of the line = 2/√41, 6/√41, -1/√41.
Example : Find the direction cosines of the line joining the points (2,1,2) and (4,2,0).
Solution:
Let the points are A(2,1,2) and B(4,2,0).
x2-x1 = 4-2 = 2
y2-y1 = 2-1 = 1
z2-z1 = 0-2 = -2
AB = √(22+12+(-2)2)= 3
Hence the direction cosines are ⅔, ⅓, -⅔.
Example : Find the direction cosines of the line joining the points (2,3,-1) and (3,-2,1).
Solution:
Let the points are A(2,3,-1) and B(3,-2,1).
x2-x1 = 3-2 = 1
y2-y1 = -2-3 = -5
z2-z1 = 1- (-1) = 2
AB = √(12+(-5)2+22)= √30
Hence the direction cosines are 1/√30, -5/√30, 2/√30.
2. Concepts of Lines and Cartesian equation and vector equation of a line
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Concepts of Lines and Cartesian equation and vector equation of a line:
It is known that we can uniquely determine a line if:
- It passes through a particular point in a specific direction, or
- It passes through two unique points
Equation of a Line passing through a point and parallel to a vector:
Let us consider that the position vector of the given point be ![]() with respect to the origin.
with respect to the origin.
The line passing through point A is given by l and it is parallel to the vector ![]()
as shown below. Let us choose any random point R on the line l and its position vector with respect to origin of the rectangular co-ordinate system is given by 


It is vector equation of line passing through a point and parallel to a vector.
Cartesian form:
If the three-dimensional co-ordinates of the point ‘A’ are given as (x1, y1, z1) and the direction cosines of this point is given as a, b, c then considering the rectangular co-ordinates of point P as (x, y, z):
Let
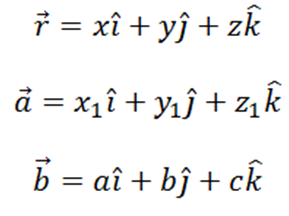
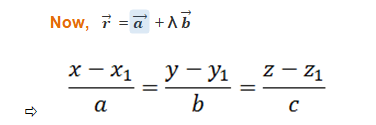
It is cartesian equation of line passing through a point and parallel to a vector.
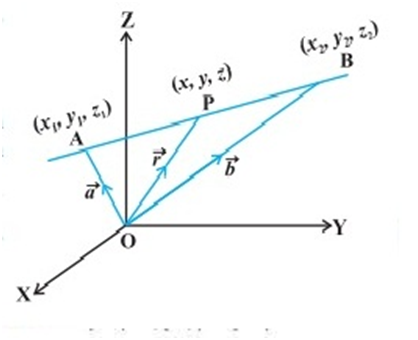
Equation of a Line passing through two unique given point:
Let us consider that the position vector of the given two point be ![]() and
and ![]() with respect to the origin.
with respect to the origin.
Let us choose any random point P on the line and its position vector with respect to origin of the rectangular co-ordinate system is given by ![]() .
.
Point P lies on the line AB if and only if the vectors ![]()
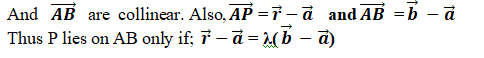
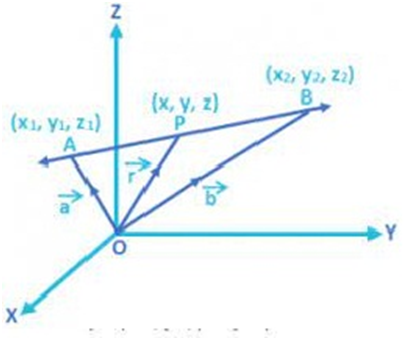
![]()
It is vector equation of line passing through two point .
Cartesian Form:

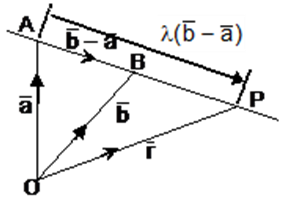
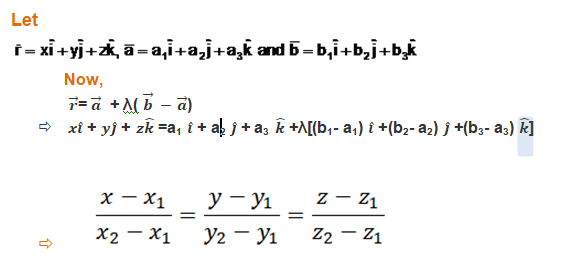
It is the Cartesian equation of a line. passing through two given points.
Example:
Find the vector and Cartesian equations of the line passing through the points A(3,4,−6) and B(5,−2,7)
Solution:
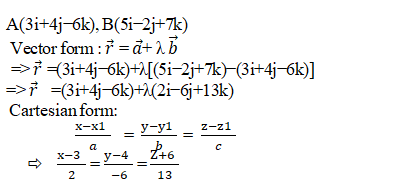
Example:
Write vector and the cartesian equations of the lines that passes through the origin and (5,−2,3)
Solution:
The line passing through (0,0,0) and (5,−2,3)

Example:
Find the cartesian equation of the line which passes through the points (7,4,6) and (9,1,8).
Solution:
Here , (x1,y1,z1) = (7,4,6) and (x2,y2,z2) = (9,1,8)
Direction ratios of the line are x2−x1 = 2, y2−y1 = -3 , z2−z1=2
Equation of line :
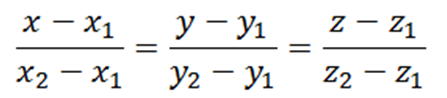
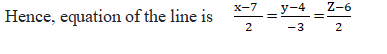
3. Angle between two lines,coplanar and skew lines
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Angle Between Two lines

Cartesian Form:
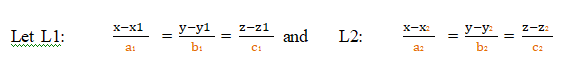
be two lines then angle between two lines is
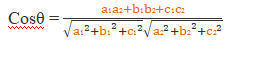
Note:- If a₁,b₁,c₁, and a₂,b₂,c₂, are the direction ratios of two lines then
i) the lines are parallel if ![]()
ii) the lines are perpendicular if ![]()
Skew lines: Skew lines are lines in space which are neither parallel nor
intersecting. They lie in different planes.
Angle between two skew lines: Angle between skew lines is the angle between
two intersecting lines drawn from any point (preferably through the origin)
parallel to each of the skew lines.
Example: Find the angle between the pair of lines given by:
(x + 3)/3 = (y – 1)/5 = (z + 3)/4 and (x + 1)/1 = (y – 4)/1 = (z – 5)/2
Answer: We can solve this problem by finding the cosine of the angle between the two lines and then taking an inverse of the cosine. Let q be the angle between the two lines. We know from the formula that:
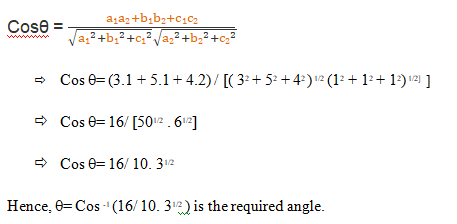
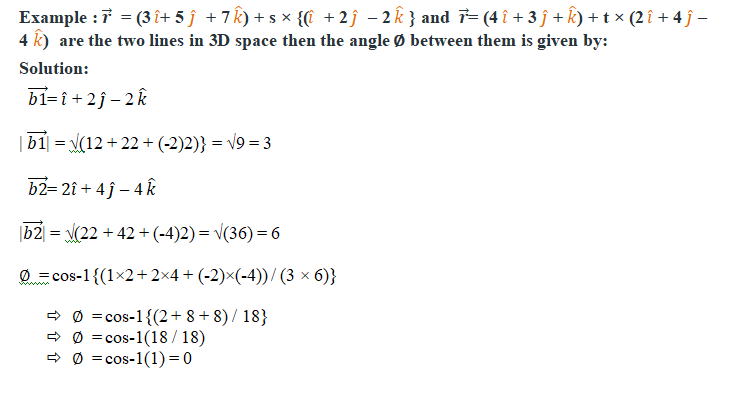
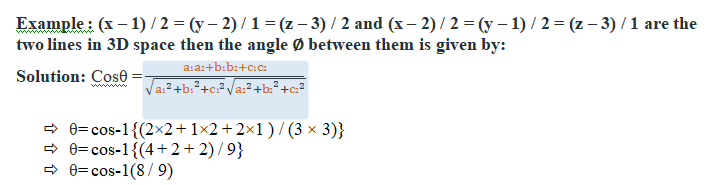
Coplanarity of Two Lines:
Coplanar lines are the lines that lie on the same plane. Prove that two lines are coplanar using the condition in vector form and Cartesian form.
Condition for Coplanarity in Vector Form
In vector form, let us consider the equations of two straight lines to be as under:
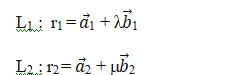
What do these equations mean? It means that the first line passes through a point, say L, whose position vector is given by ![]() and is parallel to
and is parallel to ![]() . Similarly, the second line is said to pass through another point whose position vector is given by
. Similarly, the second line is said to pass through another point whose position vector is given by ![]() and is parallel to
and is parallel to ![]()
The condition for coplanarity is that the line joining the two points must be perpendicular to the product of the two vectors, m1 and m2. To illustrate this, we know that the line joining the two said points can be written in vector form as ![]() . So, we have:
. So, we have:
![]()
Condition for Coplanarity in Cartesian Form
The derivation of the condition for coplanarity in Cartesian form stems from the vector form. Let us consider two points L (x1, y1, z1) & M (x2, y2, z2) in the Cartesian plane. Let there be two vectors ![]() and
and ![]() . Their direction ratios are given by a1, b1, c1 and a2, b2, c2 respectively.
. Their direction ratios are given by a1, b1, c1 and a2, b2, c2 respectively.
The vector equation of the line joining L and M can be given as:
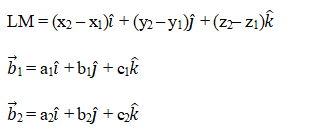
Now use the above condition in vector form to derive our condition in Cartesian form.
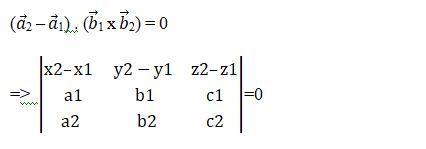
Question : Are the lines (x + 3)/3 = (y – 1)/1 = (z – 5)/5 and (x + 1)/ -1 = (y – 2)/2 = (z – 5)/5 coplanar?
Answer: Comparing the equations with the general form, we have:
(x1, y1, z1) = (-3, 1, 5) and (x2, y2, z2) = (-1, 2, 5).
Note that a1, b1, c1 = -3, 1, 5 and a2, b2, c2 = -1, 2, 5.
So, by Cartesian form, we must solve the matrix:
= 2(5 – 10) – 1(-15 + 5) + 0(-6 + 1) = -10 + 10 = 0
Since the solution of the matrix gives us 0, we can say that the given lines are coplanar
This can be used as is for calculation purposes. By the condition above, the two lines would be coplanar if LM. (m1 x m2) = 0. Therefore, in Cartesian form, the matrix representing this equation is given as 0.
4. shortest distance between two lines
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Shortest Distance between Two Lines:
- If lines are intersecting then the shortest distance is zero.
- If lines are skew lines , the line of the shortest distance will be perpendicular to both the lines.
- If lines are parallel lines , the line of the shortest distance will be perpendicular distance.
Distance between two skew lines:
In a space, there are lines which are neither intersecting nor parallel. In fact,such pair of lines are non coplanar and are called skew lines.
Vector Form
We shall consider two skew lines, say l1 and l2 and we are to calculate the distance between them. The equations of the lines are:
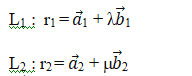

where d measures the distance or the length of the perpendicular.

Cartesian form:
The shortest distance between the lines
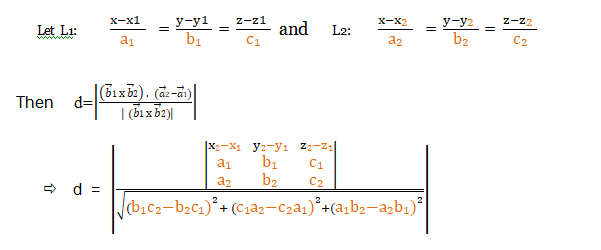
Distance between parallel lines:
If two lines l1 and l2 are parallel, then they are coplanar.
Let the lines be given by
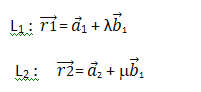

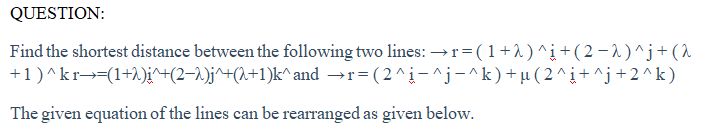
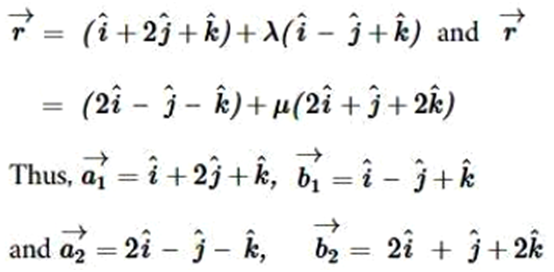
Shortest distance between LINES
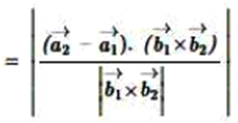
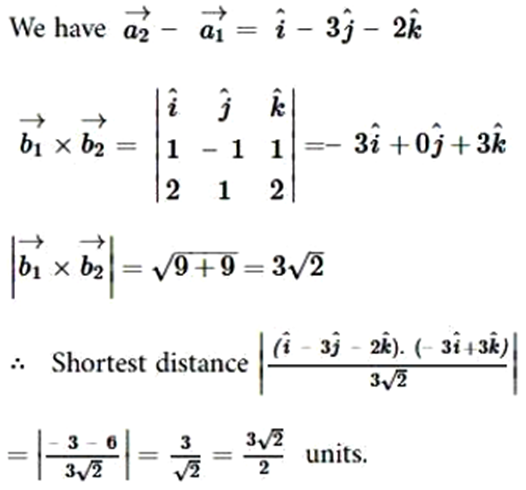
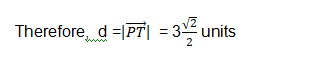
5. Concepts of Planes and Cartesian and vector equation of a plane
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Concepts of Planes and Cartesian and vector equation of a plane
Plane:
A plane is determined uniquely if any one of the following is known:
(i) the normal to the plane and its distance from the origin is given, i.e., equation of
a plane in normal form.
(ii) it passes through a point and is perpendicular to a given direction.
(iii) it passes through three given non collinear points.
Equation of a plane in normal form.:
Consider a plane whose perpendicular distance from the origin is d (d ¹ 0).

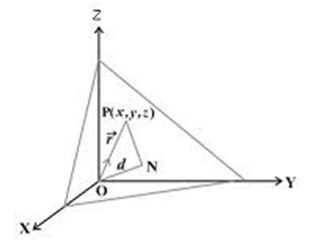
Cartesian form


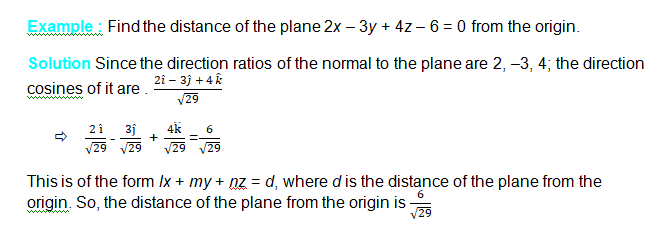
Example :Find the coordinates of the foot of the perpendicular drawn from the
origin to the plane 2x – 3y + 4z – 6 = 0.
Solution Let the coordinates of the foot of the perpendicular P from the origin to the
plane is (x1, y1,z1)
Then, the direction ratios of the line OP are
x1, y1, z1.
Since the direction ratios of the normal to the plane are 2, –3, 4;
Writing the equation of the plane in the normal

Note: If d is the distance from the origin and l, m, n are the direction cosines of the normal to the plane through the origin, then the foot of the perpendicular is (ld, md, nd).
Equation of a plane perpendicular to a given vector and passing through a given point:

Cartesian Form:
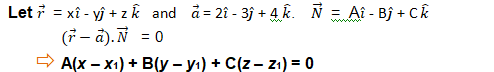
This is the cartesian equation of the plane.
Example : Find the vector and cartesian equations of the plane which passes through the point (5, 2, – 4) and perpendicular to the line with direction ratios 2, 3, – 1.

which is the Cartesian equation of the plane.
Equation of a plane passing through three non collinear points:
Let R, S and T be three non collinear points on the plane with position vectors ![]()
Respectively.
The vectors RS and RT are in the given plane. Therefore, the vector ![]()
is perpendicular to the plane containing points R, S and T. Let ![]() be the position vector
be the position vector
of any point P in the plane. Therefore, the equation of the plane passing through R and perpendicular to the vector ![]()
![]()
This is the equation of the plane in vector form passing through three non-collinear points.
Cartesian form
Let (x1, y1, z1), (x2, y2, z2) and (x3, y3, z3) be the coordinates of the points R, S and T respectively. Let (x, y, z) be the coordinates of any point P on the plane with position

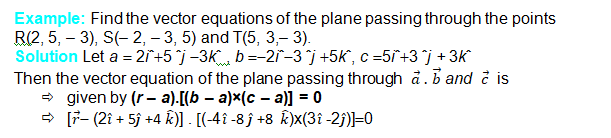
Intercept form of the equation of a plane:
Let the equation of the plane be
Ax + By + Cz + D = 0 (D ¹ 0) .................... (1)
Let the plane make intercepts a, b, c on x, y and z axes, respectively .
Hence, the plane meets x, y and z-axes at (a, 0, 0),(0, b, 0), (0, 0, c), respectively.
Plane passing through the intersection of two given planes:
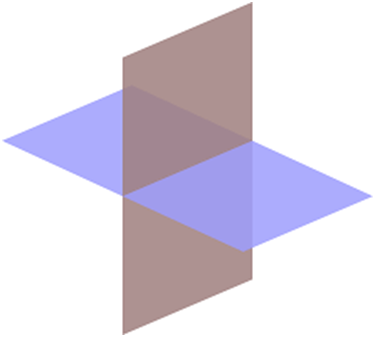
Two planes can intersect in the three-dimensional space. Imagine two adjacent pages of a book. These two pages are nothing but an intersection of planes, intersecting each other and the line between them is called the line of intersection. A new plane i.e. a third plane can be given to be passing through this line of intersection of planes. We are to find out the equation of this plane.
Let us assume that the equation of the first plane is π1 and that of the second is π2. The equation of our required plane is π and we are to find out this equation itself. This equation is given by –
![]()
The position vector of any point on the line of intersection must
satisfy both the equations.
Vector form
If the equation of the two planes is given in Vector form –
So the equation of the required plane by using (1) can be written as –
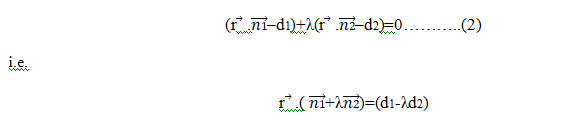
is equation of plane in vector form
Cartesian form:
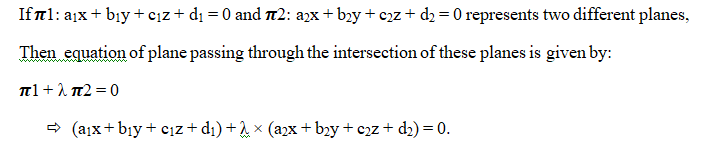
is equation of plane in cartesian form.
If a point on the required plane is given, you must substitute the coordinates for the values of x, y and z to obtain the value of λ in order to then replace it in the above equation.
Question:
The equation of the plane passing through the intersection of the planes x+y+z=6 and 2x+3y+4z+5=0, and the point (1,1,1) is
Solution:
Given equation of planes are

⇒x+y+z−6+λ(2x+3y+4z+5)=0
Given, it also passes through (1,1,1)
⇒1+1+1+−6+λ(2+3+4+5)=0⇒λ=143
Hence, required plane is, 14(x+y+z−6)+3(2x+3y+4z+5)=0
⇒20x+23y+26z−69=0
Question:
The d.r's of the line of intersection of the planes x+y+z−1 =0 and 2x+3y+4z−7 =0 are

6. Angle between two planes a line and a plane
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Angle between Two Planes:
The angle between normal to two planes is the angle between the two planes.

Cartesian form:
Let A1 x + B1 y + C1z + D1 = 0 and A2x + B2y + C2 z + D2 = 0 be the equation of two planes aligned to each other at an angle θ where A1, B1, C1 and A2, B2, C2 are the direction ratios of the normal to the planes, then the cosine of the angle between the two planes is given by:
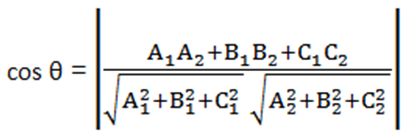
Example: Determine the angle between the two planes whose vector equations are given as r.(2i + 2j - 3k) = 4 and r.(3i - 3j + 5k) = 3.
Solution: The equations of the planes are given in vector form. Now to find the angle between the planes r.(2i + 2j - 3k) = 4 and r.(3i - 3j + 5k) = 3, we will use the formula cos θ = |(n1 . n2)|/(|n1|.|n2|). We have,
n1 = 2i + 2j - 3k, n2 = 3i - 3j + 5k
|n1| = √(22 + 22 + (-3)2) = √(4 + 4 + 9) = √17
|n2| = √(32 + (-3)2 + 52) = √(9 + 9 + 15) = √43
Scalar product of the normal vectors is given by, n1 . n2 = (2i + 2j - 3k) . (3i - 3j + 5k) = 2 × 3 + 2 × (-3) + (-3) × 5 = 6 - 6 - 15 = -15
Substituting these values into the formula, we have
cos θ = |(-15)|/(√17 . √43)
= 15/√731
⇒ θ = cos-1(15/√731)
Example: Find the angle between two planes with equations 2x + y - 2z = 5 and 3x - 6y - 2z = 7.
Solution: Since the equations of the two planes are given in the cartesian form, we will determine the angle between two planes in cartesian form using the formula cos θ = |(A1A2 + B1B2 + C1C2)|/[√(A12 + B12 + C12)√(A22 + B22 + C22)]. The equations of the planes are 2x + y - 2z = 5 and 3x - 6y - 2z = 7. Here, A1 = 2, B1 = 1, C1 = -2, A2 = 3, B2 = -6, C2 = -2. Substituting these values into the formula, we have
cos θ = (2×3 + 1×(-6) + (-2)×(-2))/[√(22 + 12 + (-2)2)√(32 + (-6)2 + (-2)2)]
= (6 + (-6) + 4)/[√(4 + 1 + 4)√(9 + 36 + 4)]
= 4/(√9 √49)
= 4/(3×7)
= 4/21
⇒ θ = cos-1(4/21)
Important Notes on Angle Between Two Planes
- The angle between two planes is equal to the angle between the normal vectors to the two planes and is called the dihedral angle.
- For planes, r.n1 = d1 and r.n2 = d2, the angle between them is given by, cos θ = |(n1 . n2)/(|n1|.|n2|)
- For planes, A1x + B1y + C1z + D1 = 0 and A2x + B2y + C2z + D2 = 0, the angle between two planes in cartesian form is given by, cos θ = |(A1A2 + B1B2 + C1C2)|/[√(A12 + B12 + C12)√(A22 + B22 + C22)]
7. Distance of a point from a plane and Distance between two planes
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Distance of a Point from a Plane
The distance between point and plane is the length of the perpendicular to the plane passing through the given point.
If we want to determine the distance between the point P with coordinates (xo, yo, zo) and the given plane with equation Ax + By + Cz = D, then the distance between point P and the given plane is given by d= |Axo + Byo+ Czo + D|/√(A2 + B2 + C2).

Example: Determine the distance between the point P = (1, 2, 5) and the plane π: 3x + 4y + z + 7 = 0
Solution: We know that the formula for distance between point and plane is: d = |Axo + Byo + Czo + D |/√(A2 + B2 + C2)
Here, A = 3, B = 4, C = 1, D = 7, xo = 1, yo = 2, zo = 5
Substituting the values in the formula, we have
d = |Axo + Byo + Czo + D |/√(A2 + B2 + C2)
= |3 × 1 + 4 × 2 + 1 × 5 + 7|/√(32 + 42 + 12)
= |3 + 8 + 5|/√(9 + 16 + 1)
= |16|/√26
= 8√26/13 units
Important Notes on Distance Between Point and Plane
- Distance Between Point and Plane Formula: |Axo + Byo + Czo + D |/√(A2 + B2 + C2)
- Distance Between Point and Plane is zero if the given point lies on the given plane.
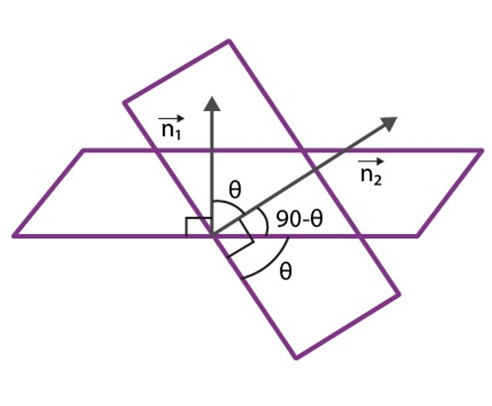
Angle between a Line and a Plane:

![]()
Let θ be the angle between the line and the normal to the plane. Its value can be given by the following equation:
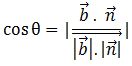
Φ is the angle between the line and the plane which is the complement of θ or 90 – θ. We know that cos θ is equal to sin (90 – θ). So Φ can be given by:
sin (90 – θ) = cos θ
or
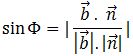
or
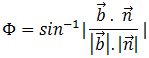
Problem: A line has an equation
![]()
The equation of a plane is 3x + 4y – 12z = 7. Find the angle between them.
Solution: Let θ be the angle between the line and the normal to the plane. In the vector form, the equations can be written as:
![]()
The equation of the plane in the vector form can be given by:
![]()
So we have
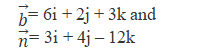
Finding the value of the Φ between the line and the plane:
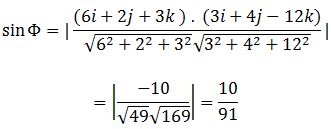
The value of Φ can be found by
![]()
Definition : The angle between a line and a plane is the complement of the angle between the line and normal to the plane

 KRISHNA PUBLICATIONS
KRISHNA PUBLICATIONS
