- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
Standard equations , Properties and Application of a ellipse
Ellipse
Definition: An ellipse is the set of all points in a plane, the sum of whose distances from two fixed points in the plane is a constant. The two fixed points are called the foci (plural of ‘focus’) of the ellipse.
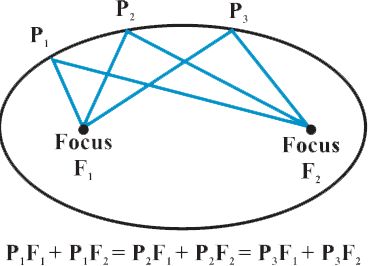
The mid point of the line segment joining the foci is called the centre of the ellipse. The line segment through the foci of the ellipse is called the major axis and the line segment through the centre and perpendicular to the major axis is called the minor axis. The end points of the major axis are called the vertices of the ellipse
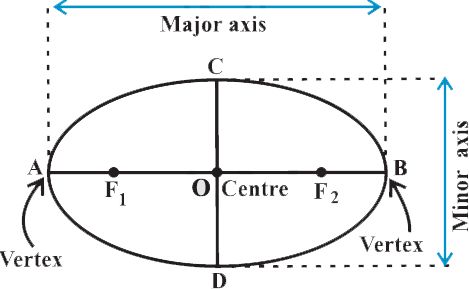
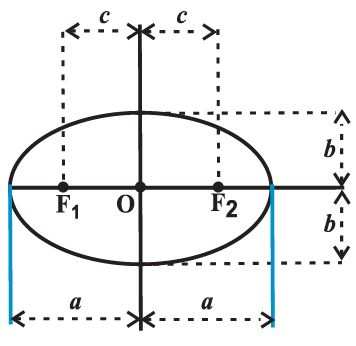
We denote the length of the major axis by 2a, the length of the minor axis by 2b and the distance between the foci by 2c. Thus, the length of the semi major axis is a and semi-minor axis is b
Relationship between semi-major axis, semi-minor axis and the distance of the focus from the centre of the ellipse:
Sum of the distances of the point P to the foci is F1 P + F2P = F1O + OP + F2P
(Since, F1P = F1O + OP)
= c + a + a – c = 2a
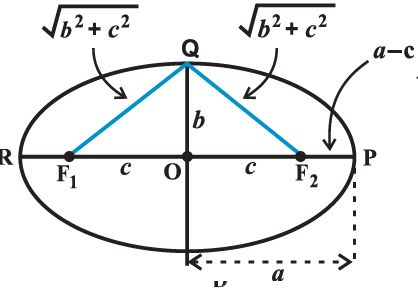
a2 = b2 + c2
Special cases of an ellipse In the equation c2 = a2 – b2 obtained above, if we keep a fixed and vary c from 0 to a, the resulting ellipses will vary in shape.
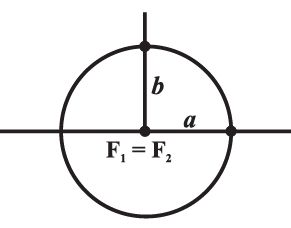
Case (i) When c = 0, both foci merge together with the centre of the ellipse and a2 = b2, i.e., a = b, and so the ellipse becomes circle . Thus, circle is a special case of an ellipse.
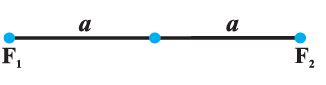
Case (ii) When c = a, then b = 0. The ellipse reduces to the line segment F1F2 joining the two foci.
Eccentricity
Definition: The eccentricity of an ellipse is the ratio of the distances from the centre of the ellipse to one of the foci and to one of the vertices of the ellipse (eccentricity is denoted by e) i.e., e= c/a
Standard equations of an ellipse The equation of an ellipse is simplest if the centre of the ellipse is at the origin and the foci are on the x-axis or y-axis.
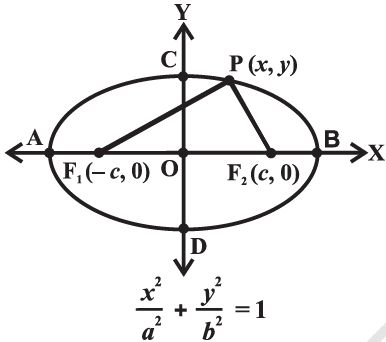
Let F1 and F2 be the foci and O be the midpoint of the line segment F1F2. Let O be the origin and the line from O through F2 be the positive x-axis and that through F1as the negative x-axis.
Let, the line through O perpendicular to the x-axis be the y-axis. Let the coordinates of F1 be (– c, 0) and F2 be (c, 0) .
Let P(x, y) be any point on the ellipse such that the sum of the distances from P to the two foci be 2a
so given PF1 + PF2 = 2a.
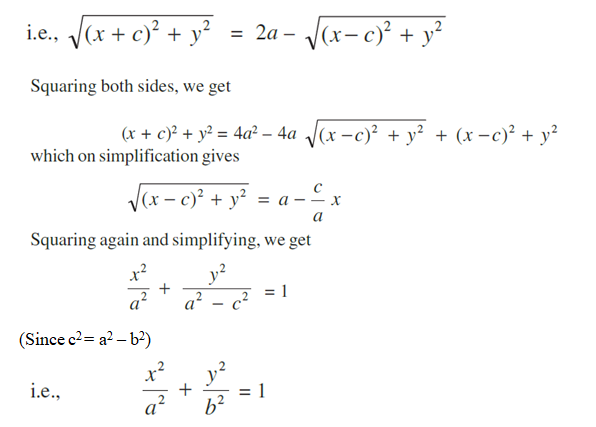
Hence any point on the ellipse satisfies satisfies
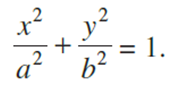
the geometric condition and so P(x, y) lies on the ellipse.
Therefore, the ellipse lies between the lines x = – a and x = a and touches these lines.
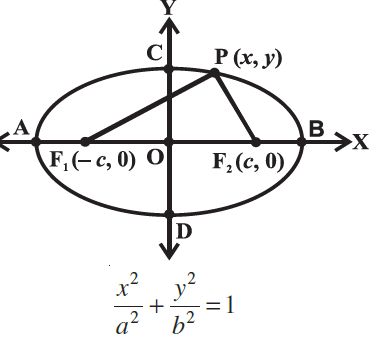
Similarly, the ellipse lies between the lines y = – b and y = b and touches these lines.
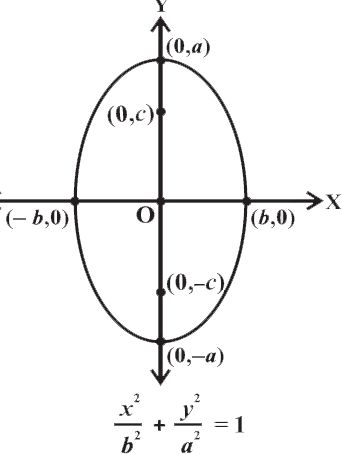
Similarly, we can derive the equation of the ellipse.
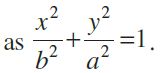
These two equations are known as standard equations of the ellipses.
Properties:
1. Ellipse is symmetric with respect to both the coordinate axes since if (x, y) is a point on the ellipse, then (– x, y), (x, –y) and (– x, –y) are also points on the ellipse.
2. The foci always lie on the major axis. The major axis can be determined by finding the intercepts on the axes of symmetry. That is, major axis is along the x-axis if the coefficient of x2 has the larger denominator and it is along the y-axis if the coefficient of y2 has the larger denominator.
Latus rectum
Definition: Latus rectum of an ellipse is a line segment perpendicular to the major axis through any of the foci and whose end points lie on the ellipse.
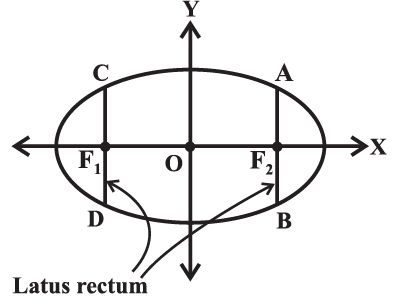
Let the length of AF2 be l. Then the coordinates of A are (c, l ),
i.e., (ae, l )
Since A lies on the ellipse
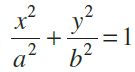
we have
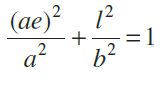
- l2 = b2 (1 – e2) but e2=c2/a2 = 1- (b2/a2)
Therefore, l2 = b4/a2
- l = b2/a
Since the ellipse is symmetric with respect to y-axis (of course, it is symmetric w.r.t. both the coordinate axes), AF2 = F2B and so length of the latus rectum is 2l =2b2/a
Example: Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the latus rectum of the ellipse
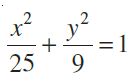
Solution Since denominator of x2/25 is larger than the denominator of y2/9 , the major
axis is along the x-axis.
a = 5 and b = 3. Also
c =√(a2 – b2)
=√(25 – 9)
=4
Therefore, the coordinates of the foci are (– 4,0) and (4,0), vertices are (– 5, 0) and
(5, 0). Length of the major axis is 10 units length of the minor axis 2b is 6 units and the
eccentricity is 4/5. and latus rectum is 2b2/a = 18 /5

 KRISHNA PUBLICATIONS
KRISHNA PUBLICATIONS
