- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
Chapter 11
Conic Sections
Sections of a cone: circle, parabola, hyperbola, ellipse:
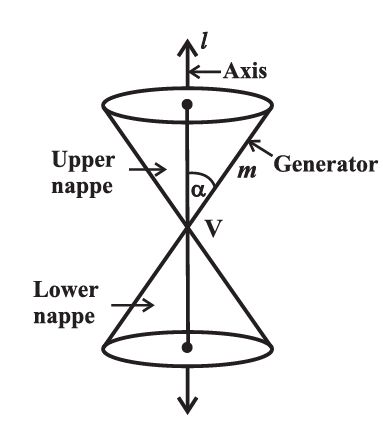
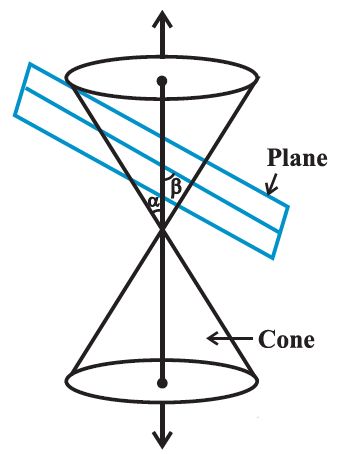
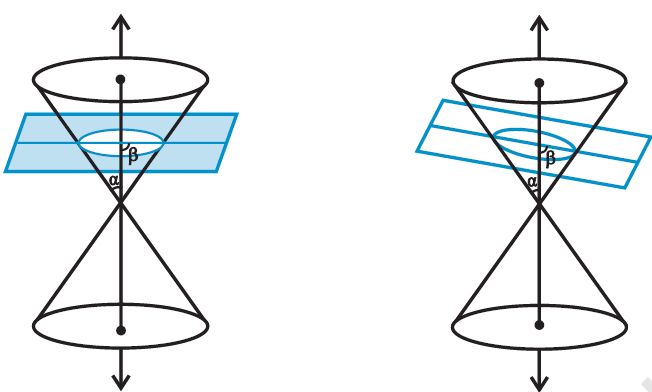
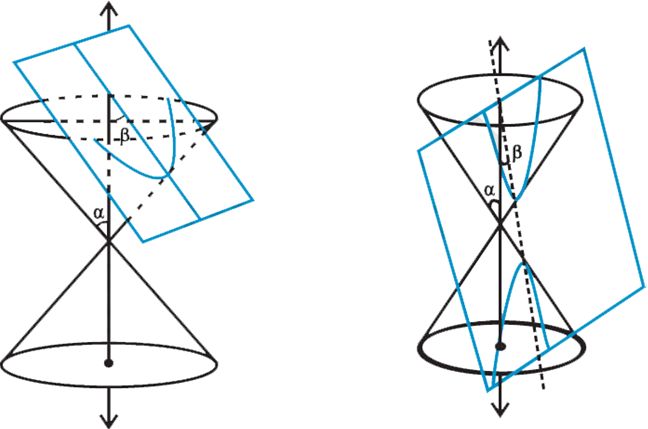
When the plane cuts the nappe (other than the vertex) of the cone, we have the following situations:
(a) When b = 90o, the section is a circle .
(b) When a < b < 90o, the section is an ellipse .
(c) When b = a; the section is a parabola .
(In each of the above three situations, the plane cuts entirely across one nappe of the cone).
(d) When 0 £ b < a; the plane cuts through both the nappes and the curves of intersection is a hyperbola .
Circle: Set of points in a plane equidistant from a fixed point. A circle with radius r and centre (h, k) can be represented as (x – h)2 + (y – k)2 = r2
Parabola: Set of points in a plane that are equidistant from a fixed-line and point. A parabola with a > 0, focus at (a, 0), and directrix x = – a can be represented as y2 = 4ax
In parabola y2 = 4ax, the length of the latus rectum is given by 4a.
Ellipse: The sum of distances of a set of points in a plane from two fixed points is constant. An ellipse with foci on the x-axis can be represented as: 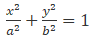
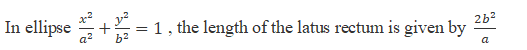
Hyperbola: The difference of distances of set of points in a plane from two fixed points is constant. The hyperbola with foci on the x-axis can be represented as: ![]()

 KRISHNA PUBLICATIONS
KRISHNA PUBLICATIONS
