- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
Standard equations , Properties and Application of a parabola
Parabola:
Definition: A parabola is the set of all points in a plane that are equidistant from a fixed line
and a fixed point (not on the line) in the plane.
The fixed line is called the directrix of the parabola and the fixed point F is called the focus 11. (‘Para’ means ‘for’ and ‘bola’ means ‘throwing’, i.e., the shape described when you throw a ball in the air).
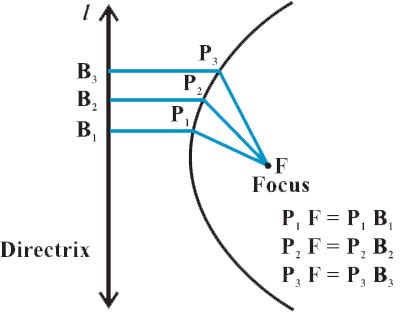
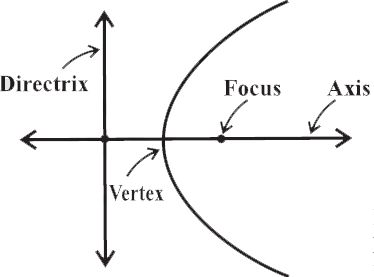
A line through the focus and perpendicular to the directrix is called the axis of the parabola.
The point of intersection of parabola with the axis is called the vertex of the parabola.
Standard equations of parabola
The equation of a parabola is simplest if the vertex is at the origin and the axis of symmetry is along the x-axis or y-axis. The four possible such orientations of parabola.
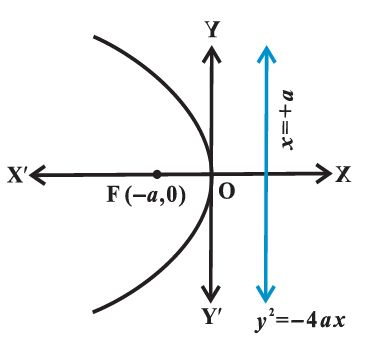
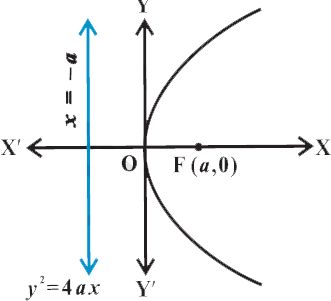
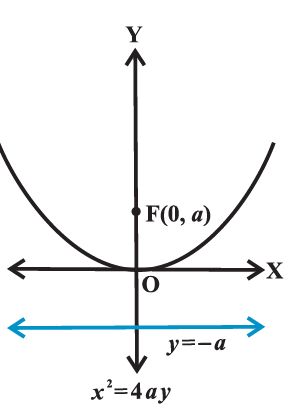
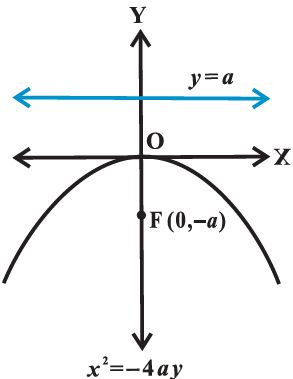
Let P(x, y) be any point on the parabola such that
PF = PB, ... (1)
where PB is perpendicular to l. The coordinates of B are (– a, y). By the distance
formula, we have
(PF) 2 = (x – a)2 + y2 and (PB) 2 = (x + a) 2
Since PF = PB, we have
(x – a) 2 + y2 = (x + a) 2
or x2 – 2ax + a2 + y2 = x2 + 2ax + a2
or y2 = 4ax ( a > 0). is Standard equation of Parabola.
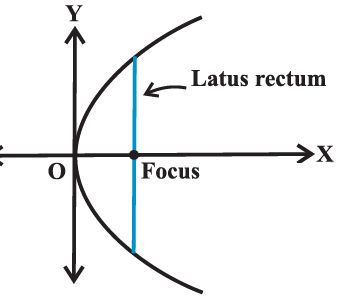
Latus rectum
Definition : Latus rectum of a parabola is a line segment perpendicular to the axis of
the parabola, through the focus and whose end points lie on the parabola .
To find the Length of the latus rectum of the parabola y2 = 4ax .
By the definition of the parabola, AF = AC.
But AC = FM = 2a
Hence AF = 2a.
And since the parabola is symmetric with respect to x-axis AF = FB and so
AB = Length of the latus rectum = 4a.
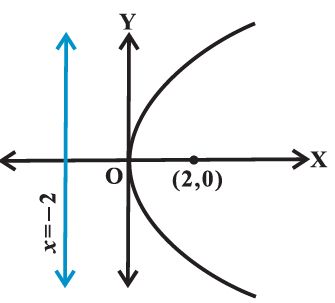
Example : Find the coordinates of the focus, axis, the equation of the directrix and latus rectum of the parabola y2 = 8x.
Solution The given equation involves y2, so the axis of symmetry is along the x-axis.
The coefficient of x is positive so the parabola opens to the right. Comparing with the given equation y2 = 4ax, we find that a = 2.
Thus, the focus of the parabola is (2, 0) and the equation of the directrix of the parabola is
x = – 2 .
Length of the latus rectum is 4a = 4 × 2 = 8.
Properties:
- Parabola is symmetric with respect to the axis of the parabola.If the equation
has a y2 term, then the axis of symmetry is along the x-axis and if the
equation has an x2 term, then the axis of symmetry is along the y-axis.
2. When the axis of symmetry is along the x-axis the parabola opens to the
(a) right if the coefficient of x is positive,
(b) left if the coefficient of x is negative.
3. When the axis of symmetry is along the y-axis the parabola opens
(c) upwards if the coefficient of y is positive.
(d) downwards if the coefficient of y is negative
Example: Find the equation of the parabola with focus (2,0) and directrix x = – 2.
Solution :Since the focus (2,0) lies on the x-axis, the x-axis itself is the axis of the
parabola. Hence the equation of the parabola is of the form either
y2 = 4ax
- y2 = – 4ax. Since the directrix is x = – 2 and the focus is (2,0), the parabola
is to be of the form y2 = 4ax with a = 2.
Hence the required equation is
y2 = 4(2)x = 8x
Example: Find the equation of the parabola with vertex at (0, 0) and focus at (0, 2).
Solution: Since the vertex is at (0,0) and the focus is at (0,2) which lies on y-axis, the
y-axis is the axis of the parabola. Therefore, equation of the parabola is of the form
x2 = 4ay. thus, we have
x2 = 4(2)y, i.e., x2= 8y.

 KRISHNA PUBLICATIONS
KRISHNA PUBLICATIONS
