Equation of Motion

Equation of Motion:

Condition: If acceleration is Constant

 

 

 

 

    Motion Under Gravity

If any mass is throwing in air then a downward gravitational force mg acts on the mass and this type of motion is known as motion under gravity.

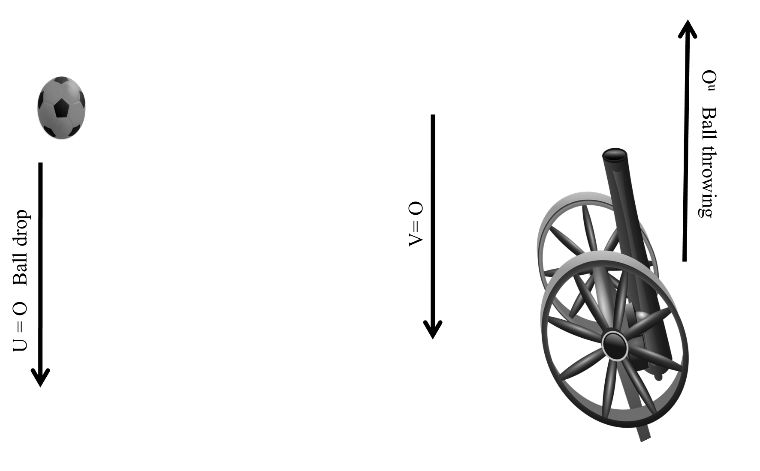
Case I:-  When ball is dropping from the top equations of motion.

V = u + gt

v² = u² + 2 gh

Ball drops from any height then its initial velocity.

                           u = 0

Case II:-  When  ball is throwing upward with initial velocity u.

Equations of motion ,

v = u – gt

v² = u² – 2gh

At the top when ball reaches its maximum height then it final velocity.

                                     V = 0

Important case (1) :-

When a ball thrown vertical upward with velocity u and it is said that distance covered by ball in t^th  sec is equal to (t + 1)^th sec.

Þ It implied that final velocity of ball v becomes zero after time t.

Example:

If a ball is throw with initial velocity u and it distance travelled by the ball in 5^th sec and 6^th sec is equal then what will be the maximum height covered by the ball.

Solution:

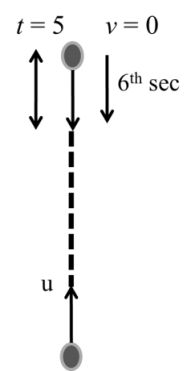
It is clear that time taken for upward motion of the ball is 5 sec there for down ward motion time will be 5 sec also.

For down ward motion    

= 125 meter   Ans

Important Case (2):-

If any object thrown vertically upward and it crosses certain height two time in a fixed interval of time.

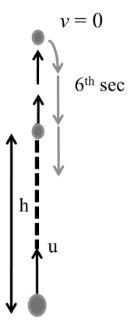
Example: A ball is thrown upward from the ground with an initial speed u. The ball is at a height of 80 meter at two times, the time interval being 6 sec. Find value of u.

Solution:-

Now,

 

5t² –ut + 80 = 0 

Now t must have two values t₁ & t₂

Using Sri Dharacharya

5t² – ut + 80 = 0

Compare with    ax² + bx + c = 0

a = 5, b = - u, c = 80

 

 

Now            t₂ – t₁ = 6

 

 

 

u² -1600 = 900

u = 50m/s

Important Case (3):-

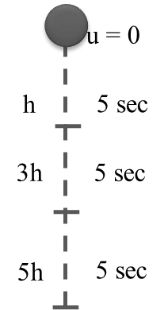
If any object starting from rest and moving with uniform acceleration has distance covered in equal interval of time will be in ratio of  1:3:5:7……….

Example:-
If body drops from a certain height and it covers h distance in first 5sec then distance covered in next 5 sec also in further next 5 sec will be = ?

Solution:- fixed time interval is 5 sec by the ratio:-

For each 5 sec

h₁ : h₂ : h₃ …. 1: 3: 5 : 7……

Important Case:- (4)

If a body starting from rest and moving with uniform acceleration then ratio of distance covered in 1sec, 2sec, 3sec…..   = 1: 4 : 9: ….

                                       = 1² : 2² : 3²….. 4²: 5²

Important Case: (5): Juggler’s moving balls.

Example: A juggler keeps on moving four balls in the air throws the balls in regular interval of time. When one ball leaves his hand with speed 20m/s the position of other balls will be (g = 10m/s²).

Solution:-

V = u – gt

O = 20 – 10t

t = 2 sec for each ball to reach max

Now for ball 1

                      

 

= 5 mt

From top so 15 mt from bottom

Maximum height

= 40 - 20

= 20 mt

Ball 1 is at 5 mt

5mt, 15mt, 20mt

Important Case (6):- Parachutist

Example: A parachutist after bailing out fells 50 meter without friction when parachute opens, it decelerates at 2m/s². He reaches the ground with a speed of 3 m/s At what height did he bail out.   (g = 9.8 ms²)

Important Case (6):- Parachutist

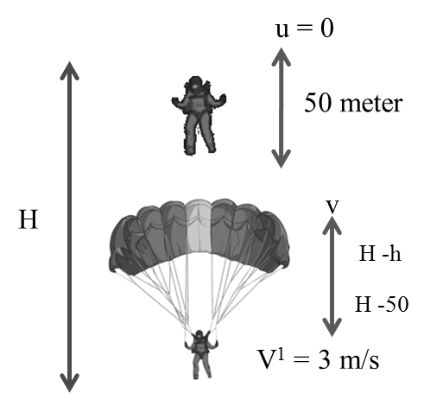
Example: A parachutist after bailing out tells 50 meter without friction when parachute opens, it decelerates at 2m/s². He reaches the ground with a speed of 3 m/s At what height did he bail out.   (g = 9.8 ms²)

Solution:-                                                  

V² = u² + 2 gh

V² = 2 x 9.8 x 50

Now after parachute opens

V² = V² -2a (H – h)

9 = 980 – 2 x 2 (H - h)

4 (H - h) = 980 – 9

  

H = 242.75 + h = 242.75 + 50

                               ≈ 293 mt.              Ans

Important Case:- (7)

Ball drops from rising balloon.

Example:- A ball is dropped from a balloon going up at a speed of 7 m/s. If the balloon was at a height 60 met at the time of dropping the ball, how long will the ball take in reaching the ground

Solution:-                                  

Using

 

Sigh convention

 

 

5t² – 7t - 60 = 0

Compare ax² + bx + c = 0

Taking  +  sigh

    

Graph of kinematics

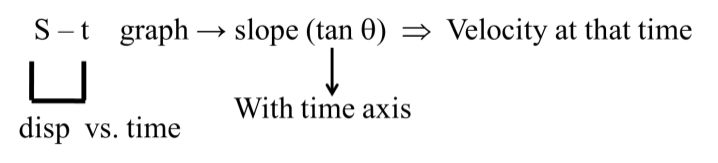
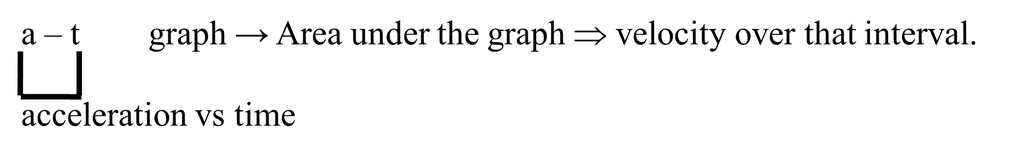
Examples:-

(1) A body is moving with constant speed (v) and covers distance (s) in time (t)

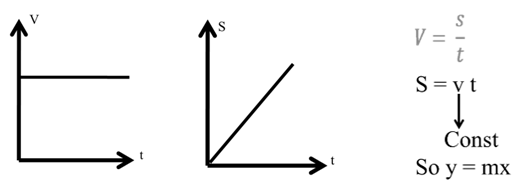
(2) A body starts from rest and moves with constant acceleration (a) attained velocity (Ѵ) and covers a displacement (s) in time t.

 Ѵ = u + at

Ѵ = o + at

 Ѵ = at

By y = mx                                                                              

(3) A body is  moving with speed u then accelerate with constant acceleration (a) and attain speed u as well as covered distance (s) in time t

Example based on graph

A train starts from rest and moves with a constant acceleration of 2 m/s² for half a minute. The breaks are then applied and trains comes to rest in one minute.

Find (i) Total distance moved by the train.

        (ii) The maximum speed attained by the train

Solution: He we will draw V-t graph

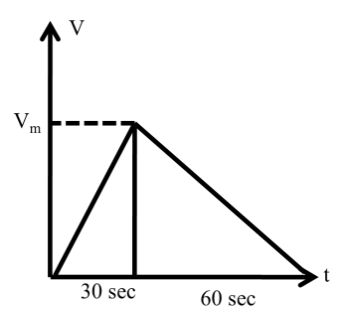
Now slope of V-t group Þ acceleration

V_max  = 60 m/s

to get total distance moved by the train we will get total area under the curve.

 

               

A₁ + A₂ = 2700 mt

             = 2.7 km                         Ans.