Kinematics

KINEMATICS
Rest and motion:-
Rest: “if position of any object or particle is not changing with respect to any observer then this object is said to be at rest”
Motion: “if position of any object or particle is changing with respect to any observers then this object is said to be in motion”
“Absolute rest and absolute motion is impossible”
Sate of rest and motion depends upon reference frame (State of observer)
Type of motion
(1) One dimensional (1-D) motion:
If position of any object is changing any of x axis, or y-axis or z axis.
All 1-D motion will be always straight line motion”
(2) Two dimensional (2-D) motion (Motion in a plane)
X-Y plane
Z- X plane
Y-Z plane
“ If position of Any object is changing in x –y or y-z or z-x plane”
Example:
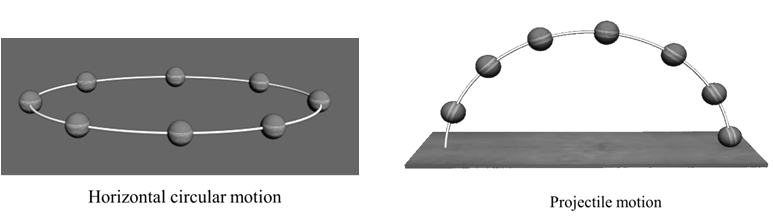
2-D motion may be straight line motion”
“Writing on board or copy is also 2-D event”
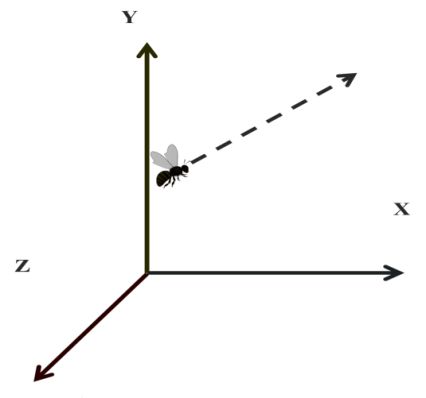
(3) Three dimensional (3-D) motion:-
“ if position of any object is changing along all 3 – axis (x-y z)”
Example:-

Human can move in 1-D, 2-D, or 3-D motion”

![]()
BASIC TERMS IN KINEMATICS
(1) Displacement:
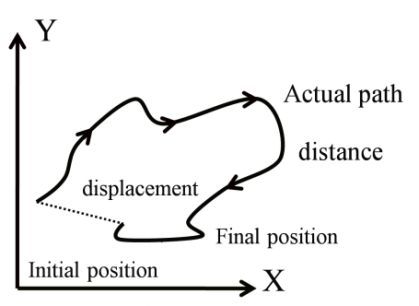
“length of straight line drawn between initial and final position
of any object”
“Shortest path between initial and final position of any object”
It is vector quantity so it may be +, - , zero.
(2) Distance:-
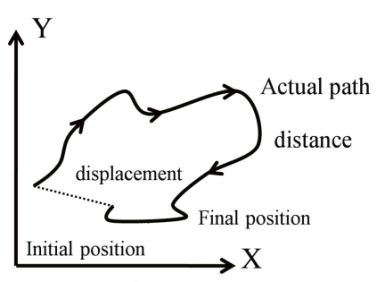
“length of actual path travelled by any object” It is scalar quantity so it will be always positive.
Distance ≥ Displacement
![]()
For straight line motion distance will equal to displacement.
UNDERSTANDING OF DISPLACEMENT AND DISTANCE
Example:-
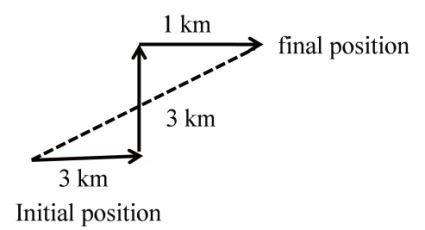
“A person is moving 3 km towards east then take left turn and move 3 km towards north then person take a right turn and move 1 km further due east and stops.
(i) What will be the total distance travelled by person.
(ii) What will be the net displacement of the person.
Solution: As we study in vectors and scalars.
(i) Distance: length of actual path so distance = 3 km + 3 km + 1 km = 7 km
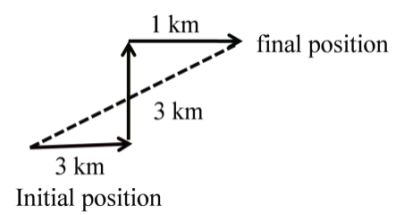
(ii) Displacement: length of straight line
First method:
![]()
![]()
![]()
Second method
![]()
Applying Pythagoras = 5 km
Example: 2 An object is moving in a circular path of radius of ![]()
meter shown in figure Find magnitude of distance
and displacement.
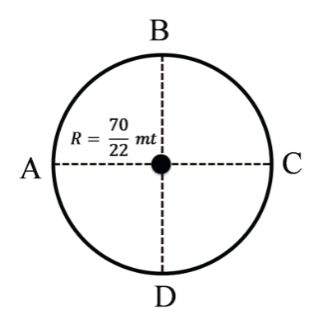
(i) From A to B
(ii) From A to C
(iii) From A to D
(iv) From A to A
Solution
A to B
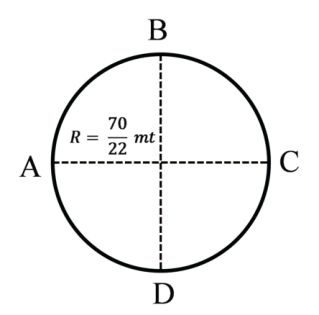
![]()
![]()
![]()
= 5 meter
![]()
![]()
A to D
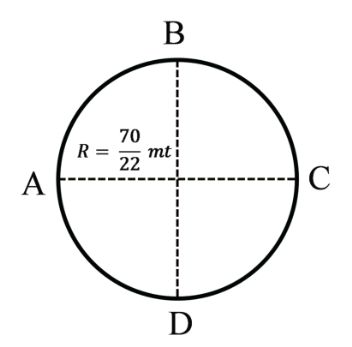
![]()
![]()
= 15 meter
![]()
![]()
A to C
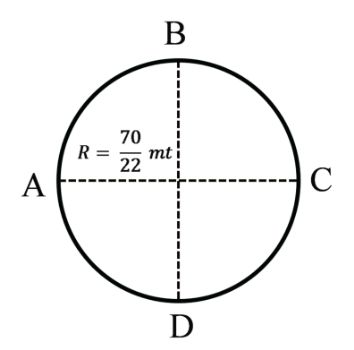
![]()
![]()
![]()
= 10 meter
![]()
![]()
A to A
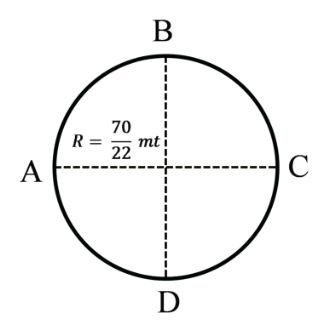
Distance = 2pR
![]()
= 20mt
Displacement = 0
Velocity
VELOCITY
“Rate of change of displacement:
Vector so may be + , - , zero ,
Unit: meter/sec , km/hr , cm/sec etc
Dimensional formula: [LT-1]
![]() condition Þ Direction of velocity and displacement must be same
condition Þ Direction of velocity and displacement must be same
![]()
Example: There are four persons are standing at the four corners of a square. Assume that all four persons start with Constant
speed v and move towards each other. Find the time when all four persons will meet to each other. If length of each side is given l.
Solution:
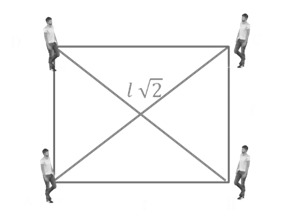
AC2 = AB2 + BC2
= l2 + l2
![]()
![]()
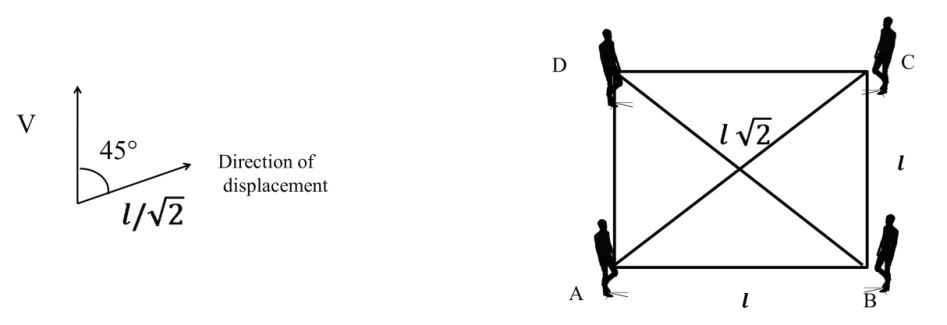
Now for person A direction of V
Component of v along direction of displacement is v ![]()
![]()
Note: General result for above Concept
Trick: If there is n person and polygon of n sides then time require to meet each other
![]()
Example. If there are 6 persons moving towards each other with Constant speed v. Initially all 6 persons standing at the Corner
of a hexagon then time required to meet
Solution: Use above result for general Case
![]()
![]()
Note: Similarly if there are three persons standing at the corners of a equilateral triangle.
![]()
MEAN OR AVERAGE VELOCITY
![]()
Case I Same time (S.T.)
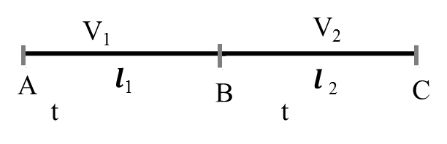
Now (Vav) AtoC = ?
![]()
![]()
![]()
![]()
![]()
As above
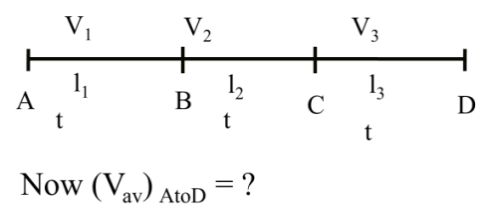
l1 = V1 t
l2 = V2t and l3 = V3 t
![]()
![]()
![]()
![]()
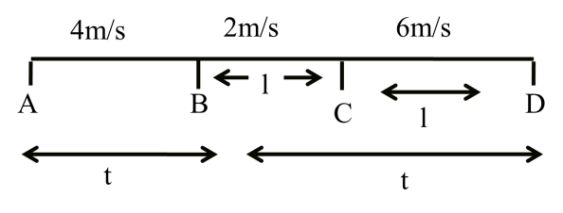
Case II Same gap (S. G.)
Now (Vav) AtoC = ?
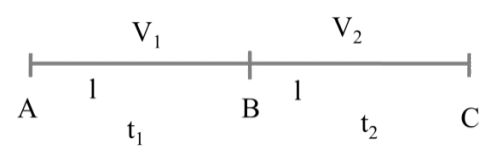
![]()
![]()
![]()
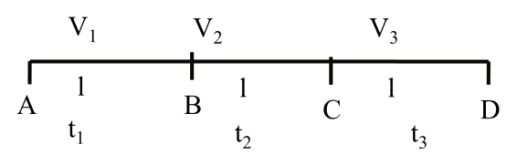
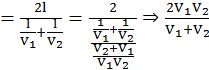
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Now Case I (S.T.) + Same gap (S.G.)
Example
Solution: Now for B to D Same gap
![]()
![]()
Acceleration:
“Rate of change of velocity
Vectors, so may be + , - , zero
Unit : met/sec2
Dimensional formula [LT-2],
![]()
Case I : Acceleration due to change in magnitude of velocity
If magnitude of velocity is increasing Þ

If magnitude of velocity is decreasing Þ

Retardation or Deceleration
Case II : Acceleration due to change in direction of velocity
![]()
![]()
![]()
![]()
![]()
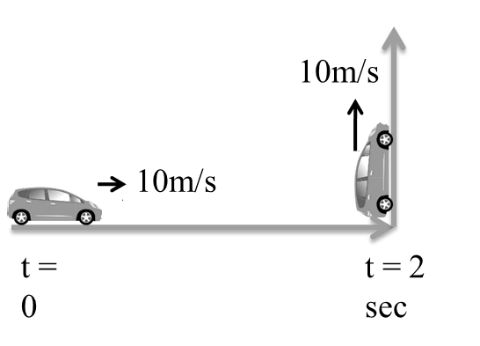
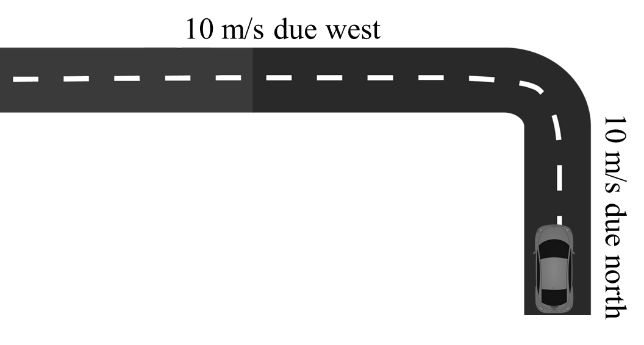
Example: A car is moving with 10 m/s due north after 2 second it take left turn and keep moving with 10m/s due west. Acceleration the Car will be
![]()
![]()
c 52m/s2 due S-E
d 52m/s2 due S-W
Solution:
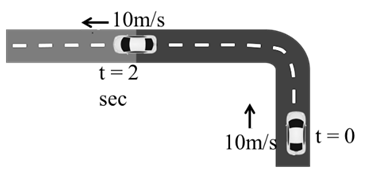
Initial velocity V1=10j m/s
Final Velocity V2=-10i m/s
Due North – West direction
a=V2-V1∆t
=-10i-10j2
a= -5i-5j
a=52 m/s2
Answer is (d)
For direction of acceleration
Ans 52 m/s2S-Wdirection
CONVERSION OF GRAPH
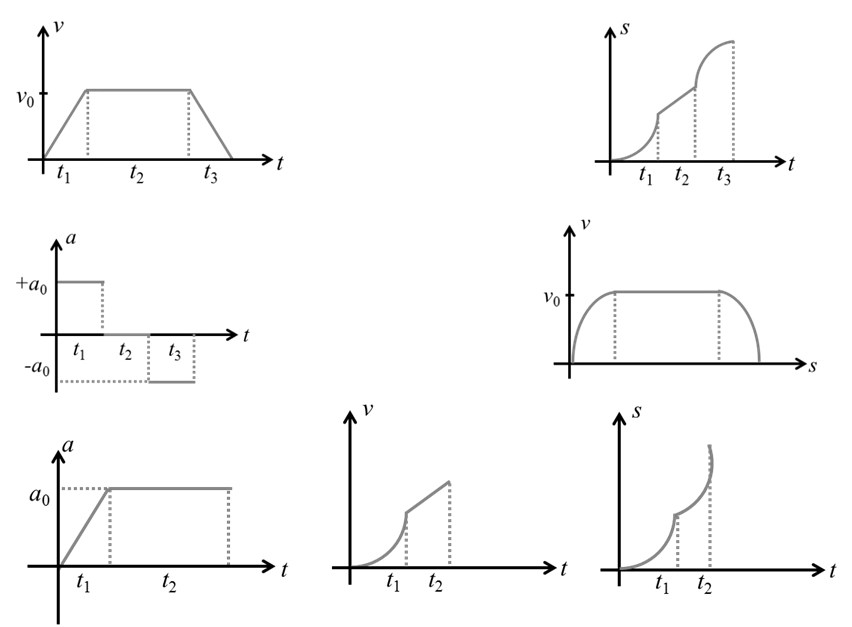
SOME IMPOSSIBLE (NON REALISTIC) GRAPH
(1) Distance never decrease

(2) Time never constant never decrease

(3) At a time no multiple values
Equation of Motion
Equation of Motion:
Condition: If acceleration is Constant
![]()
![]()
![]()
![]()
Motion Under Gravity
If any mass is throwing in air then a downward gravitational force mg acts on the mass and this type of motion is known as motion under gravity.
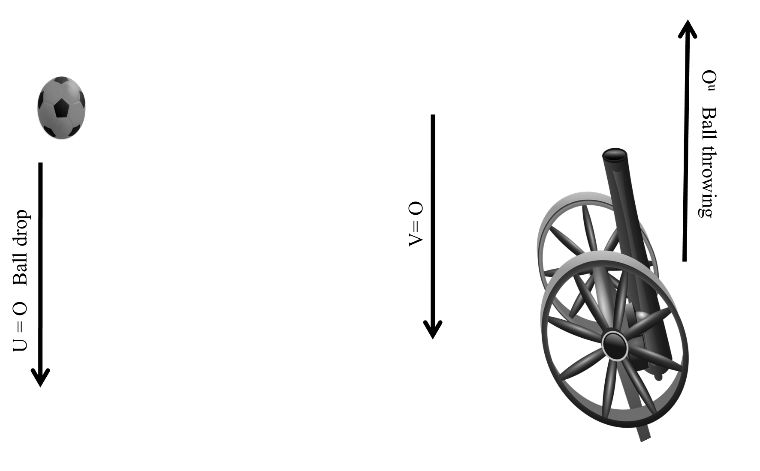
Case I:- When ball is dropping from the top equations of motion.
V = u + gt
![]()
v2 = u2 + 2 gh
Ball drops from any height then its initial velocity.
u = 0
Case II:- When ball is throwing upward with initial velocity u.
Equations of motion ,
v = u – gt
![]()
v2 = u2 – 2gh
At the top when ball reaches its maximum height then it final velocity.
V = 0
Important case (1) :-
When a ball thrown vertical upward with velocity u and it is said that distance covered by ball in tth sec is equal to (t + 1)th sec.
Þ It implied that final velocity of ball v becomes zero after time t.
Example:
If a ball is throw with initial velocity u and it distance travelled by the ball in 5th sec and 6th sec is equal then what will be the maximum height covered by the ball.
Solution:
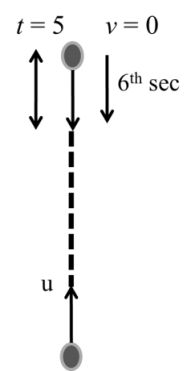
It is clear that time taken for upward motion of the ball is 5 sec there for down ward motion time will be 5 sec also.
For down ward motion
![]()
![]()
= 125 meter Ans
Important Case (2):-
If any object thrown vertically upward and it crosses certain height two time in a fixed interval of time.
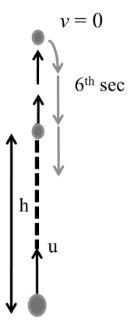
Example: A ball is thrown upward from the ground with an initial speed u. The ball is at a height of 80 meter at two times, the time interval being 6 sec. Find value of u.
Solution:-
Now,
![]()
![]()
5t2 –ut + 80 = 0
Now t must have two values t1 & t2
Using Sri Dharacharya
5t2 – ut + 80 = 0
Compare with ax2 + bx + c = 0
a = 5, b = - u, c = 80
![]()
![]()
Now t2 – t1 = 6
![]()
![]()
![]()
u2 -1600 = 900
u = 50m/s
Important Case (3):-
If any object starting from rest and moving with uniform acceleration has distance covered in equal interval of time will be in ratio of 1:3:5:7……….
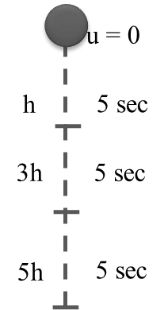
Example:-
If body drops from a certain height and it covers h distance in first 5sec then distance covered in next 5 sec also in further next 5 sec will be = ?
Solution:- fixed time interval is 5 sec by the ratio:-
For each 5 sec
h1 : h2 : h3 …. 1: 3: 5 : 7……
Important Case:- (4)
If a body starting from rest and moving with uniform acceleration then ratio of distance covered in 1sec, 2sec, 3sec….. = 1: 4 : 9: ….
= 12 : 22 : 32….. 42: 52
Important Case: (5): Juggler’s moving balls.
Example: A juggler keeps on moving four balls in the air throws the balls in regular interval of time. When one ball leaves his hand with speed 20m/s the position of other balls will be (g = 10m/s2).
Solution:-

V = u – gt
O = 20 – 10t
t = 2 sec for each ball to reach max
Now for ball 1
![]()
![]()
= 5 mt
From top so 15 mt from bottom
Maximum height
![]()
![]()
= 40 - 20
= 20 mt
Ball 1 is at 5 mt
5mt, 15mt, 20mt
Important Case (6):- Parachutist
Example: A parachutist after bailing out fells 50 meter without friction when parachute opens, it decelerates at 2m/s2. He reaches the ground with a speed of 3 m/s At what height did he bail out. (g = 9.8 ms2)
Important Case (6):- Parachutist
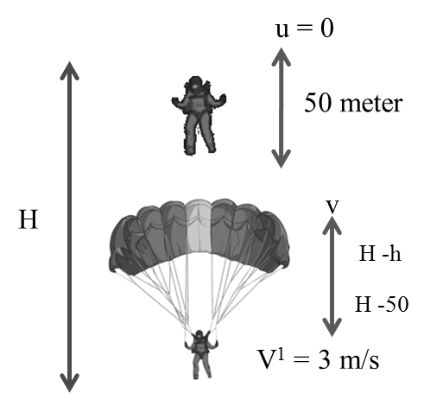
Example: A parachutist after bailing out tells 50 meter without friction when parachute opens, it decelerates at 2m/s2. He reaches the ground with a speed of 3 m/s At what height did he bail out. (g = 9.8 ms2)
Solution:-
V2 = u2 + 2 gh
V2 = 2 x 9.8 x 50
![]()
Now after parachute opens
V2 = V2 -2a (H – h)
9 = 980 – 2 x 2 (H - h)
4 (H - h) = 980 – 9
![]()
H = 242.75 + h = 242.75 + 50
≈ 293 mt. Ans
Important Case:- (7)
Ball drops from rising balloon.
Example:- A ball is dropped from a balloon going up at a speed of 7 m/s. If the balloon was at a height 60 met at the time of dropping the ball, how long will the ball take in reaching the ground
Solution:-
Using
![]()
Sigh convention

![]()
![]()
5t2 – 7t - 60 = 0
Compare ax2 + bx + c = 0
![]()
![]()
Taking + sigh
![]()
Graph of kinematics
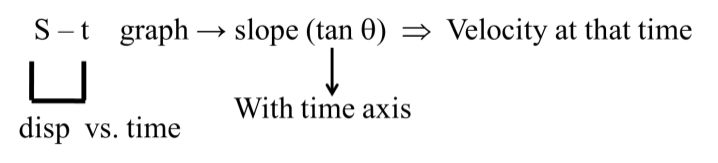

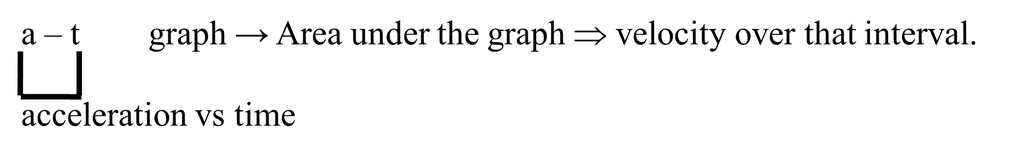
Examples:-
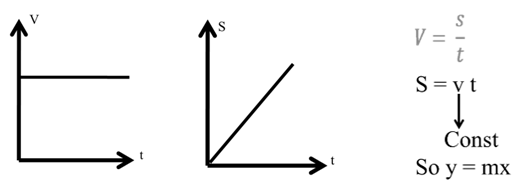
(1) A body is moving with constant speed (v) and covers distance (s) in time (t)
(2) A body starts from rest and moves with constant acceleration (a) attained velocity (Ѵ) and covers a displacement (s) in time t.

Ѵ = u + at
Ѵ = o + at
Ѵ = at
By y = mx
(3) A body is moving with speed u then accelerate with constant acceleration (a) and attain speed u as well as covered distance (s) in time t
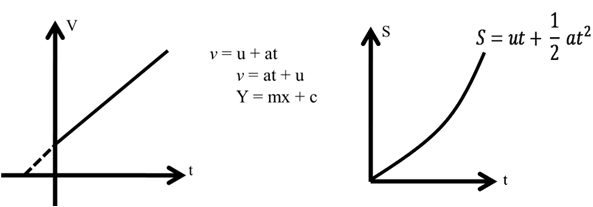
Example based on graph
A train starts from rest and moves with a constant acceleration of 2 m/s2 for half a minute. The breaks are then applied and trains comes to rest in one minute.
Find (i) Total distance moved by the train.
(ii) The maximum speed attained by the train
Solution: He we will draw V-t graph
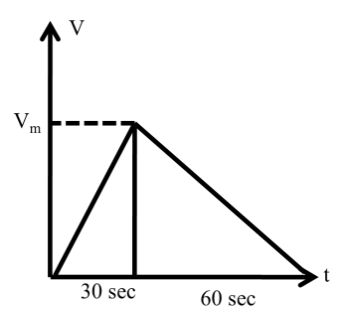
Now slope of V-t group Þ acceleration
![]()
Vmax = 60 m/s
to get total distance moved by the train we will get total area under the curve.
![]()
![]()
![]()
A1 + A2 = 2700 mt
= 2.7 km Ans.

 Kaysons Publication
Kaysons Publication
