- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
BOHR’S MODEL FOR HYDROGEN ATOM
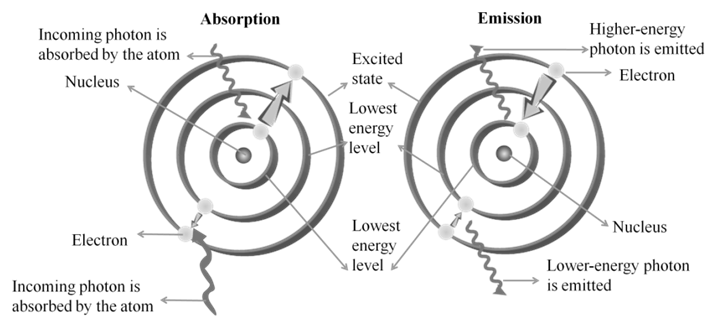
a. An electron in the hydrogen atom can move around the nucleus in a circular path of fixed radius and energy. These paths are called orbits or energy levels. These orbits are arranged concentrically around the nucleus.
b. As long as an electron remains in a particular orbit, it does not lose or gain energy and its energy remains constant.
c. When transition occurs between two stationary states that differ in energy, the frequency of the radiation absorbed or emitted can be calculated. n = DE/h = (E2-E1)/h
n= Frequency of radiation
h = Planck's constant
E1 Energy of lower energy state
E2 Energy of higher energy state
d. An electron can move only in those orbits for which its angular momentum is an integral multiple of h/2p Þ mevr = n ![]() where n = 1, 2 ,3 ….
where n = 1, 2 ,3 ….
Bohr’s theory for hydrogen atom:
a. Stationary states for electron are numbered in terms of Principal Quantum numbered as n=1, 2, 3…
b. For hydrogen atom: The radii of the stationary states is expressed as rn = n2a0 where a0= 52.9 pm
c. Energy of stationary state En = -RH![]() where n 1, 2,3,.... and RH is 2.18x10-18 ( rhydberg’s constant)
where n 1, 2,3,.... and RH is 2.18x10-18 ( rhydberg’s constant)
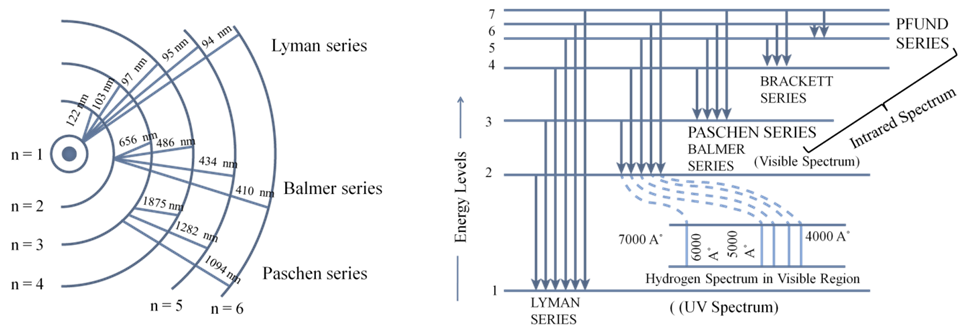
CALCULATION OF WAVELENGTH FOR HYDROGEN SPECTRUM
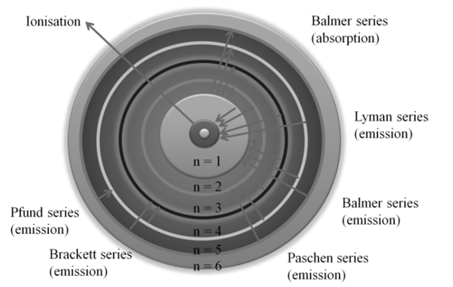
BOHR MODEL OF THE HYDROGEN ATOM
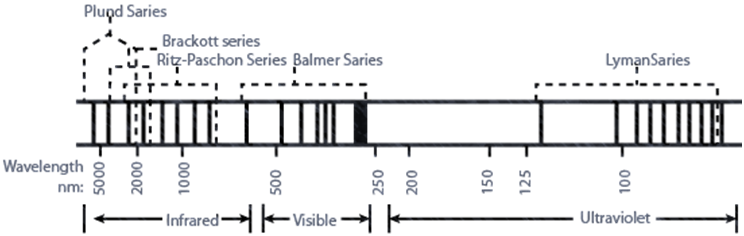

![]()
For equilibrium Þ centripetal force = centrifugal force
![]()
q1 = Ze q2 = e
![]()
On solving equation (1) & (3)
![]()
![]()
From equation (3)
Þ rn = r1 x n2 Different orbit Some Atom (DOSA)
![]() Same Orbit Different Atom (SODA)
Same Orbit Different Atom (SODA)
From equation (4)
Þ Vn = V1 / n DOSA
Þ VZ = VH x Z SODA
Total Energy = K.E. + P.E.
![]()
Putting value form equation (3) & (4) ![]()
![]()
From equation (5)
![]() D.O.S.A
D.O.S.A
![]() S.O.D.A
S.O.D.A
For Hydrogen Atom Z =1
As per Bohr model
∆E = hv
![]()
![]()
![]()
RH=109677 cm-1 and is called Rydberg’s constant
SUCCESS AND FAILURES OF BOHR’S MODEL OF ATOM
Success of Bohr’s model
1. The frequencies of spectrum in hydrogen lines were successfully explained.
2. The value of Rydberg’s constant calculated matched the experimental value.
3. It could explain the spectrum of hydrogen like species like He+, Li+2 etc
LIMITATIONS OF BOHR’S MODEL OF ATOM
-
- Bohr’s model failed to account for the finer details of the hydrogen spectrum. For instance splitting of a line in the spectrum into two closely spaced lines.
- Bohr’s model was also unable to explain spectrum of atoms containing more than one electron.
- Bohr’s model was unable to explain Zeeman Effect i.e. splitting of spectral line in presence of magnetic effect.
- Bohr’s model also failed to explain Stark effect i.e. splitting of spectral line in presence of electric field.
- Bohr’s model could not explain the ability of atoms to form molecules by chemical bonds

 Kaysons Publication
Kaysons Publication
