Polynomials in one variable
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Polynomials
Polynomials are algebraic expressions that consist of variables and coefficients. Variables are also sometimes called indeterminates. We can perform arithmetic operations such as addition, subtraction, multiplication and also positive integer exponents for polynomial expressions but not division by variable. An example of a polynomial with one variable is x2+x-12. In this example, there are three terms: x2, x and -12.
Also, Check: What is Mathematics
The word polynomial is derived from the Greek words ‘poly’ means ‘many‘ and ‘nominal’ means ‘terms‘, so altogether it said “many terms”. A polynomial can have any number of terms but not infinite. Learn about degree, terms, types, properties, polynomial functions in this article.
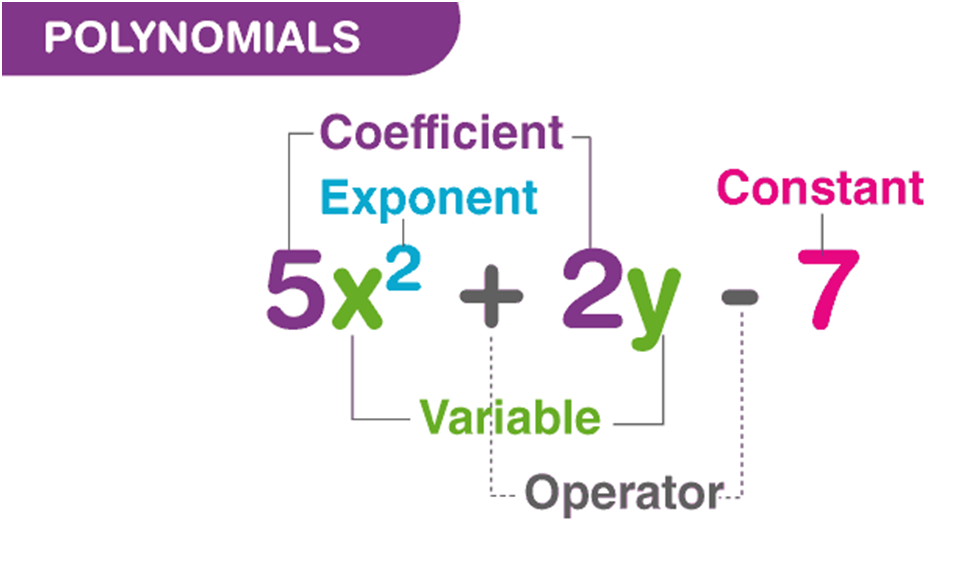
What is a Polynomial?
Polynomial is made up of two terms, namely Poly (meaning “many”) and Nominal (meaning “terms.”). A polynomial is defined as an expression which is composed of variables, constants and exponents, that are combined using the mathematical operations such as addition, subtraction, multiplication and division (No division operation by a variable). Based on the numbers of terms present in the expression, it is classified as monomial, binomial, and trinomial. Examples of constants, variables and exponents are as follows:
- Constants. Example: 1, 2, 3, etc.
- Variables. Example: g, h, x, y, etc.
- Exponents: Example: 5 in x5 etc.
Notation
The polynomial function is denoted by P(x) where x represents the variable. For example,
P(x) = x2-5x+11
If the variable is denoted by a, then the function will be P(a)
Polynomials in one variable
Chapter 2 - Polynomials
Polynomials
Polynomials are algebraic expressions that consist of variables and coefficients. Variables are also sometimes called indeterminates. We can perform arithmetic operations such as addition, subtraction, multiplication and also positive integer exponents for polynomial expressions but not division by variable. An example of a polynomial with one variable is x2+x-12. In this example, there are three terms: x2, x and -12.
Also, Check: What is Mathematics
The word polynomial is derived from the Greek words ‘poly’ means ‘many‘ and ‘nominal’ means ‘terms‘, so altogether it said “many terms”. A polynomial can have any number of terms but not infinite. Learn about degree, terms, types, properties, polynomial functions in this article.
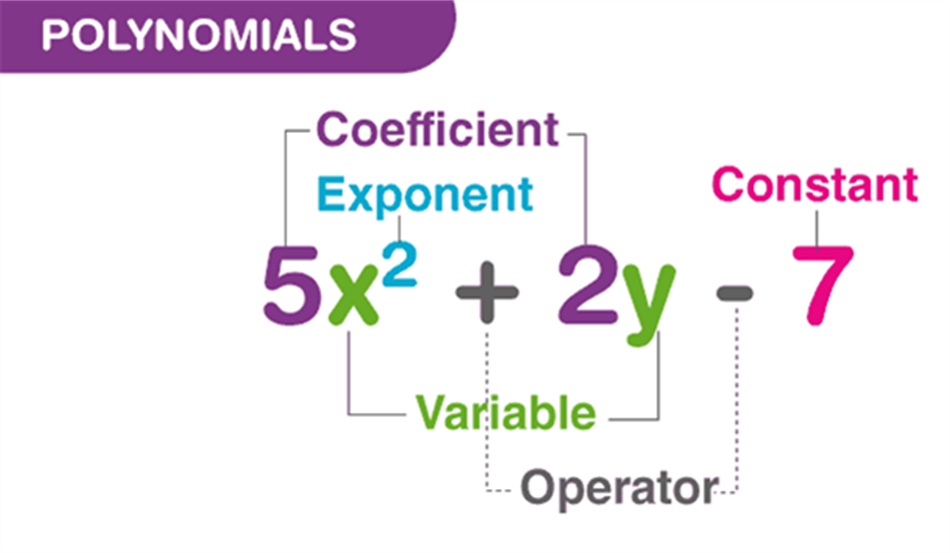
What is a Polynomial?
Polynomial is made up of two terms, namely Poly (meaning “many”) and Nominal (meaning “terms.”). A polynomial is defined as an expression which is composed of variables, constants and exponents, that are combined using the mathematical operations such as addition, subtraction, multiplication and division (No division operation by a variable). Based on the numbers of terms present in the expression, it is classified as monomial, binomial, and trinomial. Examples of constants, variables and exponents are as follows:
- Constants. Example: 1, 2, 3, etc.
- Variables. Example: g, h, x, y, etc.
- Exponents: Example: 5 in x5 etc.
Notation
The polynomial function is denoted by P(x) where x represents the variable. For example,
P(x) = x2-5x+11
If the variable is denoted by a, then the function will be P(a)
Remainder Theorem
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Remainder Theorem
Remainder Theorem is an approach to Euclidean division of polynomials. According to this theorem, if we divide a polynomial P(x) by a factor ( x – a); that isn’t essentially an element of the polynomial; you will find a smaller polynomial along with a remainder. This remainder that has been obtained is actually a value of P(x) at x = a, specifically P(a). So basically, x -a is the divisor of P(x) if and only if P(a) = 0. It is applied to factorize polynomials of each degree in an elegant manner.
For example: if f(a) = a3-12a2-42 is divided by (a-3) then the quotient will be a2-9a-27 and the remainder is -123.
if we put, a-3 = 0
then a = 3
Hence, f(a) = f(3) = -123
Thus, it satisfies the remainder theorem.

Remainder Theorem Definition
The Remainder Theorem begins with a polynomial say p(x), where “p(x)” is some polynomial p whose variable is x. Then as per theorem, dividing that polynomial p(x) by some linear factor x – a, where a is just some number. Here go through a long polynomial division, which results in some polynomial q(x) (the variable “q” stands for “the quotient polynomial”) and a polynomial remainder is r(x). It can be expressed as:
p(x)/x-a = q(x) + r(x)
Factor Theorem
Factor Theorem is generally applied to factoring and finding the roots of polynomial equations. It is the reverse form of the remainder theorem. Problems are solved based on the application of synthetic division and then to check for a zero remainder.
When p(x) = 0 then y-x is a factor of the polynomial Or if we consider the other way, then When y-x is a factor of the polynomial then p(x) =0
Remainder Theorem Proof
Theorem functions on an actual case that a polynomial is comprehensively dividable, at least one time by its factor in order to get a smaller polynomial and ‘a’ remainder of zero. This acts as one of the simplest ways to determine whether the value ‘a’ is a root of the polynomial P(x).
That is when we divide p(x) by x-a we obtain
p(x) = (x-a)·q(x) + r(x),
as we know that Dividend = (Divisor × Quotient) + Remainder
But if r(x) is simply the constant r (remember when we divide by (x-a) the remainder is a constant)…. so we obtain the following solution, i.e
p(x) = (x-a)·q(x) + r
Observe what happens when we have x equal to a:
p(a) = (a-a)·q(a) + r
p(a) = (0)·q(a) + r
p(a) = r
Hence, proved.
Steps to Divide a Polynomial by a Non-Zero Polynomial
- First, arrange the polynomials (dividend and divisor) in the decreasing order of its degree
- Divide the first term of the dividend by the first term of the divisor to produce the first term of the quotient
- Multiply the divisor by the first term of the quotient and subtract this product from the dividend, to get the remainder.
- This remainder is the dividend now and divisor will remain same
- Again repeat from the first step, until the degree of the new dividend is less than the degree of the divisor.
Remainder Theorem of Polynomial
Let us understand the remainder theorem in polynomials with the example given below:
Divide 3x3 + x2 + 2x + 5 by x + 1.
Solution:
From the given,
Dividend = p(x) = 3x3 + x2 + 2x + 5
Divisor = g(x) = (x + 1)

Here, quotient = q(x) = 3x2 – 2x + 4
Remainder = r(x) = 1
Verification:
Given, the divisor is (x + 1), i.e. it is a factor of the given polynomial p(x).
Let x + 1 = 0
x = -1
Substituting x = -1 in p(x),
p(-1) = 3(-1)3 + (-1)2 + 2(-1) + 5
= 3(-1) + 1 – 2 + 5
= -3 + 4
= 1
Remainder = Value of p(x) at x = -1.
Hence proved the remainder theorem.
Alternatively,
p(x) = (x – a)·q(x) + r
Observe what happens when we have x equal to a:
p(a) = (a – a)·q(a) + r
Substituting the values,
p(-1) = [-1 – (-1)]·q(-1) + (-1)
p(-1) = 0.q(-1) – 1
p(-1) = -1
p(-1) = remainder
Hence proved.
Remainder Theorem Problems
Consider the following example:-
Example- Determine that x = 1 is a root of P(x),
Explanation:
It suggests that x = 1 may be a root of P(x), and (x – 1) may be a factor of P(x)
Then if we tend to divide synthetically from P(x) by (x – 1), we will get a new smaller polynomial and a remainder of zero:
|
Example: Find the root of the polynomial Solution: So, (x-4) must be a factor of Example: Find the remainder when is divided by t – 1. Solution: Here, , and the zero of t – 1 is 1. ∴ p (1) = (1)3 – 2(1)2 + 1 + 1= 2 By the Remainder Theorem, 2 is the remainder when is divided by t – 1. |
Euler Remainder Theorem
Euler’s theorem states that if n and X are two co-prime positive integers, then
Xφ(n) = 1 (mod n)
where, φ(n) is Euler’s function or Euler’s totient function, which is equal to;
φ(n) = n (1-1/a).(1-1/b).(1-1/c)
where, n is a natural number, such that n = ap. bq . cr,
Here, a, b, c are prime factors of n and p, q, r are positive integers.
|
Example: Find the Euler totient function of 35. Solution: The factors of 35 are as follows: Thus the totient function of 35 is 24. |
Questions of the form:
|
Example: Find the remainder when is divided by 35. Solution: Here m = 3, a = 76 and n = 35, In an example above we have already found the totient function of 35, which is equal to 24. Remainder of = 4 Remaining power is 4, which when divided by 35 given the resultant remainder. which is, Thus the remainder comes out to be 11. |
Factoring Polynomials: How To Factorise
Factoring polynomials is the reverse procedure of multiplication of factors of polynomials. An expression of the form axn + bxn-1 +kcxn-2 + ….+kx+ l, where each variable has a constant accompanying it as its coefficient is called a polynomial of degree ‘n’ in variable x. Thus, a polynomial is an expression in which a combination of a constant and a variable is separated by an addition or a subtraction sign.
Remainder Theorem
Remainder Theorem
Remainder Theorem is an approach of Euclidean division of polynomials. According to this theorem, if we divide a polynomial P(x) by a factor ( x – a); that isn’t essentially an element of the polynomial; you will find a smaller polynomial along with a remainder. This remainder that has been obtained is actually a value of P(x) at x = a, specifically P(a). So basically, x -a is the divisor of P(x) if and only if P(a) = 0. It is applied to factorize polynomials of each degree in an elegant manner.
For example: if f(a) = a3-12a2-42 is divided by (a-3) then the quotient will be a2-9a-27 and the remainder is -123.
if we put, a-3 = 0
then a = 3
Hence, f(a) = f(3) = -123
Thus, it satisfies the remainder theorem.

The Remainder Theorem begins with a polynomial say p(x), where “p(x)” is some polynomial p whose variable is x. Then as per theorem, dividing that polynomial p(x) by some linear factor x – a, where a is just some number. Here go through a long polynomial division, which results in some polynomial q(x) (the variable “q” stands for “the quotient polynomial”) and a polynomial remainder is r(x). It can be expressed as:
p(x)/x-a = q(x) + r(x)
Factor Theorem
Factor Theorem is generally applied to factoring and finding the roots of polynomial equations. It is the reverse form of the remainder theorem. Problems are solved based on the application of synthetic division and then to check for a zero remainder.
When p(x) = 0 then y-x is a factor of the polynomial Or if we consider the other way, then When y-x is a factor of the polynomial then p(x) =0
Theorem functions on an actual case that a polynomial is comprehensively dividable, at least one time by its factor in order to get a smaller polynomial and ‘a’ remainder of zero. This acts as one of the simplest ways to determine whether the value ‘a’ is a root of the polynomial P(x).
That is when we divide p(x) by x-a we obtain
p(x) = (x-a)·q(x) + r(x),
as we know that Dividend = (Divisor × Quotient) + Remainder
But if r(x) is simply the constant r (remember when we divide by (x-a) the remainder is a constant)…. so we obtain the following solution, i.e
p(x) = (x-a)·q(x) + r
Observe what happens when we have x equal to a:
p(a) = (a-a)·q(a) + r
p(a) = (0)·q(a) + r
p(a) = r
Hence, proved.
Steps to Divide a Polynomial by a Non-Zero Polynomial
- First, arrange the polynomials (dividend and divisor) in the decreasing order of its degree
- Divide the first term of the dividend by the first term of the divisor to produce the first term of the quotient
- Multiply the divisor by the first term of the quotient and subtract this product from the dividend, to get the remainder.
- This remainder is the dividend now and divisor will remain same
- Again repeat from the first step, until the degree of the new dividend is less than the degree of the divisor.
Remainder Theorem of Polynomial
Let us understand the remainder theorem in polynomials with the example given below:
Divide 3x3 + x2 + 2x + 5 by x + 1.
Solution:
From the given,
Dividend = p(x) = 3x3 + x2 + 2x + 5
Divisor = g(x) = (x + 1)
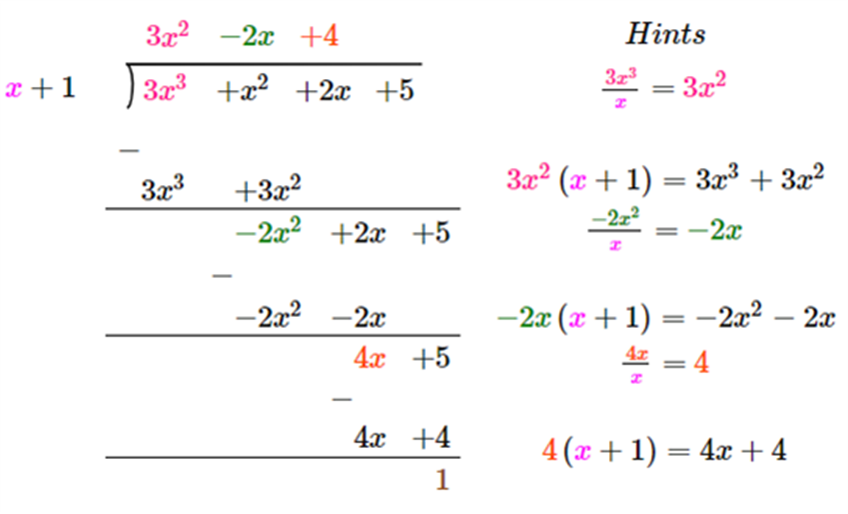
Here, quotient = q(x) = 3x2 – 2x + 4
Remainder = r(x) = 1
Verification:
Given, the divisor is (x + 1), i.e. it is a factor of the given polynomial p(x).
Let x + 1 = 0
x = -1
Substituting x = -1 in p(x),
p(-1) = 3(-1)3 + (-1)2 + 2(-1) + 5
= 3(-1) + 1 – 2 + 5
= -3 + 4
= 1
Remainder = Value of p(x) at x = -1.
Hence proved the remainder theorem.
Alternatively,
p(x) = (x – a)·q(x) + r
Observe what happens when we have x equal to a:
p(a) = (a – a)·q(a) + r
Substituting the values,
p(-1) = [-1 – (-1)]·q(-1) + (-1)
p(-1) = 0.q(-1) – 1
p(-1) = -1
p(-1) = remainder
Hence proved.
Remainder Theorem Problems
Consider the following example:-
Example- Determine that x = 1 is a root of P(x),
Explanation:
It suggests that x = 1 may be a root of P(x), and (x – 1) may be a factor of P(x)
Then if we tend to divide synthetically from P(x) by (x – 1), we will get a new smaller polynomial and a remainder of zero:
|
Example: Find the root of the polynomial Solution: So, (x-4) must be a factor of Example: Find the remainder when is divided by t – 1. Solution: Here, , and the zero of t – 1 is 1. ∴ p (1) = (1)3 – 2(1)2 + 1 + 1= 2 By the Remainder Theorem, 2 is the remainder when is divided by t – 1. |
Euler Remainder Theorem
Euler’s theorem states that if n and X are two co-prime positive integers, then
Xφ(n) = 1 (mod n)
where, φ(n) is Euler’s function or Euler’s totient function, which is equal to;
φ(n) = n (1-1/a).(1-1/b).(1-1/c)
where, n is a natural number, such that n = ap. bq . cr,
Here, a, b, c are prime factors of n and p, q, r are positive integers.
|
Example: Find the Euler totient function of 35. Solution: The factors of 35 are as follows: Thus the totient function of 35 is 24. |
Questions of the form:
|
Example: Find the remainder when is divided by 35. Solution: Here m = 3, a = 76 and n = 35, In an example above we have already found the totient function of 35, which is equal to 24. Remainder of = 4 Remaining power is 4, which when divided by 35 given the resultant remainder. which is, Thus the remainder comes out to be 11. |
Factoring Polynomials: How To Factorise
Factoring polynomials is the reverse procedure of multiplication of factors of polynomials. An expression of the form axn + bxn-1 +kcxn-2 + ….+kx+ l, where each variable has a constant accompanying it as its coefficient is called a polynomial of degree ‘n’ in variable x. Thus, a polynomial is an expression in which a combination of a constant and a variable is separated by an addition or a subtraction sign.
Factorisation of Polynomials
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Factorization of Polynomial
The process of finding factors of a given value or mathematical expression is called factorization. Factors are the integers that are multiplied to produce an original number. For example, the factors of 18 are 2, 3, 6, 9 and 18, such as;
18 = 2 x 9
18 = 2 x 3 x 3
18 = 3 x 6
Similarly, in the case of polynomials, the factors are the polynomials which are multiplied to produce the original polynomial. For example, the factors of x2 + 5x + 6 is (x + 2) (x + 3). When we multiply both x +2 and x+3, then the original polynomial is generated. After factorization, we can also find the zeros of the polynomials. In this case, zeroes are x = -2 and x = -3.
Types of Factoring polynomials
There are six different methods for factorizing polynomials. The six methods are as follows:
- Greatest Common Factor (GCF)
- Grouping Method
- Sum or difference in two cubes
- Difference in two squares method
- General trinomials
- Trinomial method
In this article, let us discuss the two basic methods which we are using frequently to factorize the polynomial. Those two methods are the greatest common factor method and the grouping method. Apart from these methods, we can factorize the polynomials by the use of general algebraic identities. Similarly, if the polynomial is of a quadratic expression, we can use the quadratic equation to find the roots/factor of a given expression. The formula to find the factors of the quadratic expression (ax2+bx+c) is given by:
How to Solve Polynomials?
There are a certain number of methods by which we can solve polynomials. Let us discuss these methods.
Greatest Common Factor
We have to find out the greatest common factor, of the given polynomial to factorize it. This process is nothing but a type of reverse procedure of distributive law, such as;
p( q + r) = pq + pr
But in the case of factorization, it is just an inverse process;
pq + pr = p(q + r)
where p is the greatest common factor.
Factoring Polynomials By Grouping
This method is also said to be factoring by pairs. Here, the given polynomial is distributed in pairs or grouped in pairs to find the zeros. Let us take an example.
Example: Factorise x2-15x+50
Find the two numbers which when added gives -15 and when multiplied gives 50.
So, -5 and -10 are the two numbers, such that;
(-5) + (-10) = -15
(-5) x (-10) = 50
Hence, we can write the given polynomial as;
x2-5x-10x+50
x(x-5)-10(x-5)
Taking x – 5 as common factor we get;
(x-5)(x-10)
Hence, the factors are (x – 5) and (x – 10).
Factoring Using Identities
The factorisation can be done also by using algebraic identities. The most common identities used in terms of the factorisation are:
- (a + b)2 = a2 + 2ab + b2
- (a – b)2 = a2 – 2ab + b2
- a2 – b2= (a + b)(a – b)
Let us see an example:
Factorise (x2 – 112)
Using the identity, we can write the above polynomial as;
(x+11) (x-11)
Factor theorem
For a polynomial p(x) of degree greater than or equal to one,
- x-a is a factor of p(x), if p(a) = 0
- If p(a) = 0, then x-a is a factor of p(x)
Where ‘a’ is a real number.
Factoring Polynomial with Four Terms
Let us learn how to factorize the polynomial having four terms. For example, x3 + x2 – x – 1 is the polynomial.
Break the given polynomial into two parts first.
(x3 + x2)+( –x – 1)
Now find the highest common factor from both the parts and take that factor out of the bracket.
We can see, from the first part, x2 is the greatest common factor and from the second part we can take out the minus sign. Thus,
x2(x+1)-1(x+1)
Again, regrouping the terms as the factors.
(x2-1) (x+1)Therefore, the factorisation of x3+ x2 – x – 1 gives (x2 -1) (x+1)
Solved Examples
Question 1:
Check whether x+3 is a factor of x3 + 3x2 + 5x +15.
Solution:
Let x + 3= 0
=> x = -3
Now, p(x) = x3 + 3x2 + 5x +15
Let us check the value of this polynomial for x = -3.
p(-3) = (-3)3 + 3 (-3)2 + 5(-3) + 15 = -27 + 27 – 15 + 15 = 0
As, p(-3) = 0, x+3 is a factor of x3 + 3x2 + 5x +15.
Factoring By Splitting the Middle Term
Question 2:
Factorize x2 + 5x + 6.
Solution:
Let us try factorizing this polynomial using splitting the middle term method.
Factoring polynomials by splitting the middle term:
In this technique we need to find two numbers ‘a’ and ‘b’ such that a + b =5 and ab = 6.
On solving this we obtain, a = 3 and b = 2
Thus, the above expression can be written as:
x2 + 3x + 2x + 6 = x(x + 3) + 2(x + 3) = (x + 3)(x + 2)
Thus, x+3 and x+2 are the factors of the polynomial x2 + 5x + 6.
Factorisation of Polynomials
Factorisation of Polynomial
The process of finding factors of a given value or mathematical expression is called factorisation. Factors are the integers that are multiplied to produce an original number. For example, the factors of 18 are 2, 3, 6, 9 and 18, such as;
18 = 2 x 9
18 = 2 x 3 x 3
18 = 3 x 6
Similarly, in the case of polynomials, the factors are the polynomials which are multiplied to produce the original polynomial. For example, the factors of x2 + 5x + 6 is (x + 2) (x + 3). When we multiply both x +2 and x+3, then the original polynomial is generated. After factorisation, we can also find the zeros of the polynomials. In this case, zeroes are x = -2 and x = -3.
Types of Factoring polynomials
There are six different methods to factorising polynomials. The six methods are as follows:
- Greatest Common Factor (GCF)
- Grouping Method
- Sum or difference in two cubes
- Difference in two squares method
- General trinomials
- Trinomial method
In this article, let us discuss the two basic methods which we are using frequently to factorise the polynomial. Those two methods are the greatest common factor method and the grouping method. Apart from these methods, we can factorise the polynomials by the use of general algebraic identities. Similarly, if the polynomial is of a quadratic expression, we can use the quadratic equation to find the roots/factor of a given expression. The formula to find the factors of the quadratic expression (ax2+bx+c) is given by:
How to Solve Polynomials?
There are a certain number of methods by which we can solve polynomials. Let us discuss these methods.
Greatest Common Factor
We have to find out the greatest common factor, of the given polynomial to factorise it. This process is nothing but a type of reverse procedure of distributive law, such as;
p( q + r) = pq + pr
But in the case of factorisation, it is just an inverse process;
pq + pr = p(q + r)
where p is the greatest common factor.
Factoring Polynomials By Grouping
This method is also said to be factoring by pairs. Here, the given polynomial is distributed in pairs or grouped in pairs to find the zeros. Let us take an example.
Example: Factorise x2-15x+50
Find the two numbers which when added gives -15 and when multiplied gives 50.
So, -5 and -10 are the two numbers, such that;
(-5) + (-10) = -15
(-5) x (-10) = 50
Hence, we can write the given polynomial as;
x2-5x-10x+50
x(x-5)-10(x-5)
Taking x – 5 as common factor we get;
(x-5)(x-10)
Hence, the factors are (x – 5) and (x – 10).
Factoring Using Identities
The factorisation can be done also by using algebraic identities. The most common identities used in terms of the factorisation are:
- (a + b)2 = a2 + 2ab + b2
- (a – b)2 = a2 – 2ab + b2
- a2 – b2= (a + b)(a – b)
Let us see an example:
Factorise (x2 – 112)
Using the identity, we can write the above polynomial as;
(x+11) (x-11)
Factor theorem
For a polynomial p(x) of degree greater than or equal to one,
- x-a is a factor of p(x), if p(a) = 0
- If p(a) = 0, then x-a is a factor of p(x)
Where ‘a’ is a real number.
Factoring Polynomial with Four Terms
Let us learn how to factorize the polynomial having four terms. For example, x3 + x2 – x – 1 is the polynomial.
Break the given polynomial into two parts first.
(x3 + x2)+( –x – 1)
Now find the highest common factor from both the parts and take that factor out of the bracket.
We can see, from the first part, x2 is the greatest common factor and from the second part we can take out the minus sign. Thus,
x2(x+1)-1(x+1)
Again, regrouping the terms as the factors.
(x2-1) (x+1)Therefore, the factorisation of x3+ x2 – x – 1 gives (x2 -1) (x+1)
Solved Examples
Question 1:
Check whether x+3 is a factor of x3 + 3x2 + 5x +15.
Solution:
Let x + 3= 0
=> x = -3
Now, p(x) = x3 + 3x2 + 5x +15
Let us check the value of this polynomial for x = -3.
p(-3) = (-3)3 + 3 (-3)2 + 5(-3) + 15 = -27 + 27 – 15 + 15 = 0
As, p(-3) = 0, x+3 is a factor of x3 + 3x2 + 5x +15.
Factoring By Splitting the Middle Term
Question 2:
Factorize x2 + 5x + 6.
Solution:
Let us try factorizing this polynomial using splitting the middle term method.
Factoring polynomials by splitting the middle term:
In this technique we need to find two numbers ‘a’ and ‘b’ such that a + b =5 and ab = 6.
On solving this we obtain, a = 3 and b = 2
Thus, the above expression can be written as:
x2 + 3x + 2x + 6 = x(x + 3) + 2(x + 3) = (x + 3)(x + 2)
Thus, x+3 and x+2 are the factors of the polynomial x2 + 5x + 6.
Zeros of a polynomial.
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
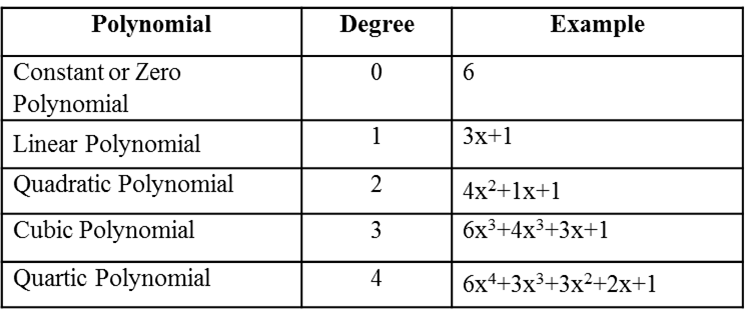
Degree of a Polynomial
The degree of a polynomial is defined as the highest degree of a monomial within a polynomial. Thus, a polynomial equation having one variable which has the largest exponent is called a degree of the polynomial.
|
Polynomial |
Degree |
Example |
|
Constant or Zero Polynomial |
0 |
6 |
|
Linear Polynomial |
1 |
3x+1 |
|
Quadratic Polynomial |
2 |
4x2+1x+1 |
|
Cubic Polynomial |
3 |
6x3+4x3+3x+1 |
|
Quartic Polynomial |
4 |
6x4+3x3+3x2+2x+1 |
Example: Find the degree of the polynomial 6s4+ 3x2+ 5x +19
Solution:
The degree of the polynomial is 4.
Terms of a Polynomial
The terms of polynomials are the parts of the equation which are generally separated by “+” or “-” signs. So, each part of a polynomial in an equation is a term. For example, in a polynomial, say, 2x2 + 5 +4, the number of terms will be 3. The classification of a polynomial is done based on the number of terms in it.
|
Polynomial |
Terms |
Degree |
|
P(x) = x3-2x2+3x+4 |
x3, -2x2, 3x and 4 |
3 |
Types of Polynomials
Polynomials are of 3 different types and are classified based on the number of terms in it. The three types of polynomials are:
- Monomial
- Binomial
- Trinomial
These polynomials can be combined using addition, subtraction, multiplication, and division but is never division by a variable. A few examples of Non Polynomials are: 1/x+2, x-3
Monomial
A monomial is an expression that contains only one term. For an expression to be a monomial, the single term should be a non-zero term. A few examples of monomials are:
- 5x
- 3
- 6a4
- -3xy
Binomial
A binomial is a polynomial expression that contains exactly two terms. A binomial can be considered as a sum or difference between two or more monomials. A few examples of binomials are:
- – 5x+3,
- 6a4 + 17x
- xy2+xy
Trinomial
A trinomial is an expression that is composed of exactly three terms. A few examples of trinomial expressions are:
- – 8a4+2x+7
- 4x2 + 9x + 7
|
Monomial |
Binomial |
Trinomial |
|
One Term |
Two terms |
Three terms |
|
Example: x, 3y, 29, x/2 |
Example: x2+x, x3-2x, y+2 |
Example: x2+2x+20 |
Properties
Some of the important properties of polynomials along with some important polynomial theorems are as follows:
Property 1: Division Algorithm
If a polynomial P(x) is divided by a polynomial G(x) results in quotient Q(x) with remainder R(x), then,
P(x) = G(x) • Q(x) + R(x)
Property 2: Bezout’s Theorem
Polynomial P(x) is divisible by binomial (x – a) if and only if P(a) = 0.
Property 3: Remainder Theorem
If P(x) is divided by (x – a) with remainder r, then P(a) = r.
Property 4: Factor Theorem
A polynomial P(x) divided by Q(x) results in R(x) with zero remainders if and only if Q(x) is a factor of P(x).
Property 5: Intermediate Value Theorem
If P(x) is a polynomial, and P(x) ≠ P(y) for (x < y), then P(x) takes every value from P(x) to P(y) in the closed interval [x, y].
Property 6
The addition, subtraction and multiplication of polynomials P and Q result in a polynomial where,
Degree(P ± Q) ≤ Degree(P or Q)
Degree(P × Q) = Degree(P) + Degree(Q)
Property 7
If a polynomial P is divisible by a polynomial Q, then every zero of Q is also a zero of P.
Property 8
If a polynomial P is divisible by two coprime polynomials Q and R, then it is divisible by (Q • R).
Property 9
If P(x) = a0 + a1x + a2x2 + …… + anxn is a polynomial such that deg(P) = n ≥ 0 then, P has at most “n” distinct roots.
Property 10: Descartes’ Rule of Sign
The number of positive real zeroes in a polynomial function P(x) is the same or less than by an even number as the number of changes in the sign of the coefficients. So, if there are “K” sign changes, the number of roots will be “k” or “(k – a)”, where “a” is some even number.
Property 11: Fundamental Theorem of Algebra
Every non-constant single-variable polynomial with complex coefficients has at least one complex root.
Property 12
If P(x) is a polynomial with real coefficients and has one complex zero (x = a – bi), then x = a + bi will also be a zero of P(x). Also, x2 – 2ax + a2 + b2 will be a factor of P(x).
Polynomial Equations
The polynomial equations are those expressions which are made up of multiple constants and variables. The standard form of writing a polynomial equation is to put the highest degree first then, at last, the constant term. An example of a polynomial equation is:
b = a4 +3a3 -2a2 +a +1
Polynomial Functions
A polynomial function is an expression constructed with one or more terms of variables with constant exponents. If there are real numbers denoted by a, then function with one variable and of degree n can be written as:
|
f(x) = a0xn + a1xn-1 + a2xn-2 + ….. + an-2x2 + an-1x + an |
Solving Polynomials
Any polynomial can be easily solved using basic algebra and factorization concepts. While solving the polynomial equation, the first step is to set the right-hand side as 0. The explanation of a polynomial solution is explained in two different ways:
- Solving Linear Polynomials
- Solving Quadratic Polynomials
Solving Linear Polynomials
Getting the solution of linear polynomials is easy and simple. First, isolate the variable term and make the equation as equal to zero. Then solve as basic algebra operation. An example of finding the solution of a linear equation is given below:
Example: Solve 3x – 9
Solution:
First, make the equation as 0. So,
3x – 9 = 0
⇒ 3x = 9
⇒ x = 9/3
Or, x = 3.
Thus, the solution of 3x-9 is x = 3.
Solving Quadratic Polynomials
To solve a quadratic polynomial, first, rewrite the expression in the descending order of degree. Then, equate the equation and perform polynomial factorization to get the solution of the equation. An example to find the solution of a quadratic polynomial is given below for better understanding.
Example: Solve 3x2 – 6x + x3 – 18
Solution:
First, arrange the polynomial in the descending order of degree and equate to zero.
⇒ x3 + 3x2 -6x – 18 = 0
Now, take the common terms.
x2(x+3) – 6(x+3) =0
⇒ (x2-6)(x+3)=0
So, the solutions will be x =-3 and
x2 = 6
Or, x = √6
For a polynomial, there could be some values of the variable for which the polynomial will be zero. These values are called zeros of a polynomial. Sometimes, they are also referred to as roots of the polynomials. In general, we find the zeros of quadratic equations, to get the solutions for the given equation.
The standard form of a polynomial in x is anxn + an-1xn-1 +….. + a1x + a0, where an, an-1, ….. , a1, a0 are constants, an ≠0 and n is a whole number. For example, algebraic expressions such as √x + x + 5, x2 + 1/x2 are not polynomials because all exponents of x in terms of the expressions are not whole numbers.
Zeros of a polynomial can be defined as the points where the polynomial becomes zero as a whole. A polynomial having value zero (0) is called zero polynomial. The degree of a polynomial is the highest power of the variable x.
- A polynomial of degree 1 is known as a linear polynomial.
The standard form is ax + b, where a and b are real numbers and a≠0.
2x + 3 is a linear polynomial. - A polynomial of degree 2 is known as a quadratic polynomial.
Standard form is ax2 + bx + c, where a, b and c are real numbers and a ≠ 0
x2+ 3x + 4 is an example for quadratic polynomial. - Polynomial of degree 3 is known as a cubic polynomial.
Standard form is ax3+ bx2 + cx + d, where a, b, c and d are real numbers and a≠0.
x3 + 4x + 2 is an example for cubic polynomial.
Similarly,
y6 + 3y4 + y is a polynomial in y of degree 6.
Formula
Consider, P(x) = 4x + 5 to be a linear polynomial in one variable.
Let ‘a’ be zero of P(x), then,
P(a) = 4k+5 = 0
Therefore, k = -5/4
In general, if k is zero of the linear polynomial in one variable: P(x) = ax +b, then;
P(k) = ak+b = 0
k = -b/a
It can also be written as,
Zero of Polynomial K = -(Constant/ Coefficient of x)
Solved Example
Example 1: What is the value of ‘a’ if degree of polynomial, x3 + xa-4 + x2 + 1, is 4?
Solution:
Degree of a polynomial P(x) is the highest power of x in P(x).
Therefore, xa-4 = x4
a-4 = 4, a = 4+4 =8
Therefore, the value of ‘a’ is 8.
Note: In general; if P(x) is a polynomial in x and k is any real number, then the value of P(k) at x = k is denoted by P(k) is found by replacing x by k in P(x).
Example 2: In the polynomial x2 – 3x + 2,
Replacing x by 1 gives,
P(1) = 1 – 3 + 2 = 0
Similarly, replacing x by 2 gives,
P(2) = 4-6+2 = 0
For a polynomial P(x), real number k is said to be zero of polynomial P(x), if P(k) = 0.
Therefore, 1 and 2 are the zeros of polynomial x2 – 3x + 2.
Zeros of a polynomial.
Degree of a Polynomial
The degree of a polynomial is defined as the highest degree of a monomial within a polynomial. Thus, a polynomial equation having one variable which has the largest exponent is called a degree of the polynomial.
Example: Find the degree of the polynomial 6s4+ 3x2+ 5x +19
Solution:
The degree of the polynomial is 4.
Terms of a Polynomial
The terms of polynomials are the parts of the equation which are generally separated by “+” or “-” signs. So, each part of a polynomial in an equation is a term. For example, in a polynomial, say, 2x2 + 5 +4, the number of terms will be 3. The classification of a polynomial is done based on the number of terms in it.

Types of Polynomials
Polynomials are of 3 different types and are classified based on the number of terms in it. The three types of polynomials are:
- Monomial
- Binomial
- Trinomial
These polynomials can be combined using addition, subtraction, multiplication, and division but is never division by a variable. A few examples of Non Polynomials are: 1/x+2, x-3
Monomial
A monomial is an expression which contains only one term. For an expression to be a monomial, the single term should be a non-zero term. A few examples of monomials are:
- 5x
- 3
- 6a4
- -3xy
Binomial
A binomial is a polynomial expression which contains exactly two terms. A binomial can be considered as a sum or difference between two or more monomials. A few examples of binomials are:
- – 5x+3,
- 6a4 + 17x
- xy2+xy
Trinomial
A trinomial is an expression which is composed of exactly three terms. A few examples of trinomial expressions are:
- – 8a4+2x+7
- 4x2 + 9x + 7

Properties
Some of the important properties of polynomials along with some important polynomial theorems are as follows:
Property 1: Division Algorithm
If a polynomial P(x) is divided by a polynomial G(x) results in quotient Q(x) with remainder R(x), then,
P(x) = G(x) • Q(x) + R(x)
Property 2: Bezout’s Theorem
Polynomial P(x) is divisible by binomial (x – a) if and only if P(a) = 0.
Property 3: Remainder Theorem
If P(x) is divided by (x – a) with remainder r, then P(a) = r.
Property 4: Factor Theorem
A polynomial P(x) divided by Q(x) results in R(x) with zero remainders if and only if Q(x) is a factor of P(x).
Property 5: Intermediate Value Theorem
If P(x) is a polynomial, and P(x) ≠ P(y) for (x < y), then P(x) takes every value from P(x) to P(y) in the closed interval [x, y].
Property 6
The addition, subtraction and multiplication of polynomials P and Q result in a polynomial where,
Degree(P ± Q) ≤ Degree(P or Q)
Degree(P × Q) = Degree(P) + Degree(Q)
Property 7
If a polynomial P is divisible by a polynomial Q, then every zero of Q is also a zero of P.
Property 8
If a polynomial P is divisible by two coprime polynomials Q and R, then it is divisible by (Q • R).
Property 9
If P(x) = a0 + a1x + a2x2 + …… + anxn is a polynomial such that deg(P) = n ≥ 0 then, P has at most “n” distinct roots.
Property 10: Descartes’ Rule of Sign
The number of positive real zeroes in a polynomial function P(x) is the same or less than by an even number as the number of changes in the sign of the coefficients. So, if there are “K” sign changes, the number of roots will be “k” or “(k – a)”, where “a” is some even number.
Property 11: Fundamental Theorem of Algebra
Every non-constant single-variable polynomial with complex coefficients has at least one complex root.
Property 12
If P(x) is a polynomial with real coefficients and has one complex zero (x = a – bi), then x = a + bi will also be a zero of P(x). Also, x2 – 2ax + a2 + b2 will be a factor of P(x).
Polynomial Equations
The polynomial equations are those expressions which are made up of multiple constants and variables. The standard form of writing a polynomial equation is to put the highest degree first then, at last, the constant term. An example of a polynomial equation is:
b = a4 +3a3 -2a2 +a +1
Polynomial Functions
A polynomial function is an expression constructed with one or more terms of variables with constant exponents. If there are real numbers denoted by a, then function with one variable and of degree n can be written as:
f(x) = a0xn + a1xn-1 + a2xn-2 + ….. + an-2x2 + an-1x + an
Solving Polynomials
Any polynomial can be easily solved using basic algebra and factorization concepts. While solving the polynomial equation, the first step is to set the right-hand side as 0. The explanation of a polynomial solution is explained in two different ways:
- Solving Linear Polynomials
- Solving Quadratic Polynomials
Solving Linear Polynomials
Getting the solution of linear polynomials is easy and simple. First, isolate the variable term and make the equation as equal to zero. Then solve as basic algebra operation. An example of finding the solution of a linear equation is given below:
Example: Solve 3x – 9
Solution:
First, make the equation as 0. So,
3x – 9 = 0
⇒ 3x = 9
⇒ x = 9/3
Or, x = 3.
Thus, the solution of 3x-9 is x = 3.
Solving Quadratic Polynomials
To solve a quadratic polynomial, first, rewrite the expression in the descending order of degree. Then, equate the equation and perform polynomial factorization to get the solution of the equation. An example to find the solution of a quadratic polynomial is given below for better understanding.
Example: Solve 3x2 – 6x + x3 – 18
Solution:
First, arrange the polynomial in the descending order of degree and equate to zero.
⇒ x3 + 3x2 -6x – 18 = 0
Now, take the common terms.
x2(x+3) – 6(x+3) =0
⇒ (x2-6)(x+3)=0
So, the solutions will be x =-3 and
x2 = 6
Or, x = √6
For a polynomial, there could be some values of the variable for which the polynomial will be zero. These values are called zeros of a polynomial. Sometimes, they are also referred to as roots of the polynomials. In general, we find the zeros of quadratic equations, to get the solutions for the given equation.
The standard form of a polynomial in x is anxn + an-1xn-1 +….. + a1x + a0, where an, an-1, ….. , a1, a0 are constants, an ≠0 and n is a whole number. For example, algebraic expressions such as √x + x + 5, x2 + 1/x2 are not polynomials because all exponents of x in terms of the expressions are not whole numbers.
Zeros of a polynomial can be defined as the points where the polynomial becomes zero as a whole. A polynomial having value zero (0) is called zero polynomial. The degree of a polynomial is the highest power of the variable x.
- A polynomial of degree 1 is known as a linear polynomial.
The standard form is ax + b, where a and b are real numbers and a≠0.
2x + 3 is a linear polynomial. - A polynomial of degree 2 is known as a quadratic polynomial.
Standard form is ax2 + bx + c, where a, b and c are real numbers and a ≠ 0
x2+ 3x + 4 is an example for quadratic polynomial. - Polynomial of degree 3 is known as a cubic polynomial.
Standard form is ax3+ bx2 + cx + d, where a, b, c and d are real numbers and a≠0.
x3 + 4x + 2 is an example for cubic polynomial.
Similarly,
y6 + 3y4 + y is a polynomial in y of degree 6.
Formula
Consider, P(x) = 4x + 5 to be a linear polynomial in one variable.
Let ‘a’ be zero of P(x), then,
P(a) = 4k+5 = 0
Therefore, k = -5/4
In general, if k is zero of the linear polynomial in one variable: P(x) = ax +b, then;
P(k) = ak+b = 0
k = -b/a
It can also be written as,
Zero of Polynomial K = -(Constant/ Coefficient of x)
Solved Example
Example 1: What is the value of ‘a’ if degree of polynomial, x3 + xa-4 + x2 + 1, is 4?
Solution:
Degree of a polynomial P(x) is the highest power of x in P(x).
Therefore, xa-4 = x4
a-4 = 4, a = 4+4 =8
Therefore, the value of ‘a’ is 8.
Note: In general; if P(x) is a polynomial in x and k is any real number, then the value of P(k) at x = k is denoted by P(k) is found by replacing x by k in P(x).
Example 2: In the polynomial x2 – 3x + 2,
Replacing x by 1 gives,
P(1) = 1 – 3 + 2 = 0
Similarly, replacing x by 2 gives,
P(2) = 4-6+2 = 0
For a polynomial P(x), real number k is said to be zero of polynomial P(x), if P(k) = 0.
Therefore, 1 and 2 are the zeros of polynomial x2 – 3x + 2.
We have discussed polynomials and their zeros here. To learn more about polynomials, download – The Learning App.
Algebraic Identities
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Algebraic Identities
Algebraic identities are an important set of formulas in math. They form the foundation working principle of algebra and are helpful to perform computations in simple and easy steps. Certain algebraic problems require working across numerous mathematical step to obtain the answer. Here, with the use of algebraic identities, we are able to perform the calculations without any additional steps. Many of the algebraic identities have been obtained from the binomial expansion of terms.
An algebra identity means that the left-hand side of the equation is identically equal to the right-hand side, for all values of the variables. Here we shall try to acquaint ourselves with all the algebraic identities, their proofs, and how to use these identities in our math calculations.
What Are Algebraic Identities?
Algebraic identities are equations where the value of the left-hand side of the equation is identically equal to the value of the right-hand side of the equation. Unlike algebraic expressions, algebraic identities satisfy all the values of the variables. Let us consider an example to understand this better. Consider the equations: 5x - 3 = 12, 10x - 6 = 24, and x2 + 5x + 6 = 0. These equations satisfy only a unit value and do not work for any other values of the variables. Now let us consider an equation x2 - 9 = (x + 3)(x - 3). These equations satisfy any values of x.
From this, we can clearly understand that an algebra identity has an expression that satisfies any values for the variables. The basic algebraic identities are primarily helpful to work out the numerous math problems. The four basic algebraic identities are as follows.
- (a + b)2 = a2 + 2ab + b2
- (a - b)2 = a2 - 2ab + b2
- (a + b)(a - b) = a2 - b2
- (x + a)(x + b) = x2 + x(a + b) + ab
Algebraic Identities from Binomial Expansion Formula
IThe binomial expansion based on the binomial theorem is helpful to find derive all the algebraic identities. Let us gain a brief idea of the binomial theorem expansion, which would be helpful to derive algebraic identities of higher degrees. Generally, binomial expansion is used for expansion involving two variables and with n degree. The total number of terms of the binomial expansion is (n + 1) and in the expanded form the power of the variable is reducing, and the power of the second variable is increasing in sequential terms. Each of the terms in the binomial expansion has a coefficient associated with it.
The following algebraic identities have been derived from the binomial expansion for sum and difference of variable and for a maximum power of 3 the algebraic identities have been listed below as formulas. Further algebraic identities of higher degrees and more variables can also be derived using the above binomial expansion formula.
- (a + b)2 = a2 + 2ab + b2
- (a - b)2 = a2 - 2ab + b2
- (a + b)(a - b) = a2 - b2
- (a + b)3 = a3 +3a2b + 3ab2 + b3
- (a - b)3 = a3 - 3a2b + 3ab2 - b3
- (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ac
Algebraic Identities for Factorization
Algebraic identities are greatly helpful in easily factorizing algebraic expressions. The given expression representing the expanded form of the formula can be transformed and written as a set of factors using the below algebraic identities. Some of the higher algebraic identities such as a4 - b4 can be easily derived using the basic algebraic identities a2 - b2. The below list presents a set of algebraic identities helpful for the factorization of polynomials.
- a2 - b2 = (a - b)(a + b)
- x2 + x(a + b) + ab = (x + a)(x + b)
- a3 - b3 = (a - b)(a2 + ab + b2)
- a3 + b3 = (a + b)(a2 - ab + b2)
- a4 - b4 = (a - b)(a + b)(a2 + b2)
Algebraic Identities for Three Variables
The algebraic identities for three variables also has been derived using the binomial expansion formula. Further these identities are helpful to easily work across the algebraic expressions with the least number of steps.
- a2 + b2 + c2 = (a + b + c)2 - 2(ab + bc + ac)
- a3 + b3 + c3 - 3abc = (a + b + c)(a2 + b2 + c2 - ab - ca - bc)
- (a + b)(a + c)(b + c) = (a + b + c)(ab + ac + bc) - 3abc
Apart from these simple algebraic identities listed above, there are other algebraic identities that we will use in higher grades.
Proof of Algebraic Identities
The following proofs of algebraic identities will help us to visually understand each of the identities and better understand it. Let us look at the proofs of each of the basic algebraic identities.
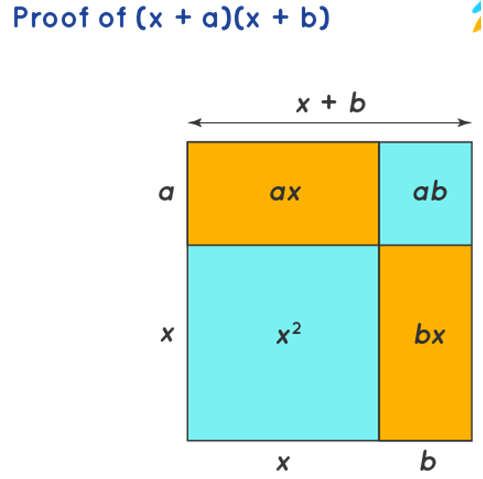
Proof of (x + a)(x + b) = x2 + x(a + b) + ab
(x+a)(x+b) is nothing but the area of a rectangle whose sides are (x+a) and (x+b) respectively. The area of a rectangle with sides (x+a) and (x+b) in terms of the individual areas of the rectangles and the square is x2, ax, bx , ab. Summing all these areas we have x2 + ax + bx + ab. This gives us the proof for the algebra identity (x + a)(x + b) = x2 + ax + bx + ab = x2 + x(a + b) + ab.
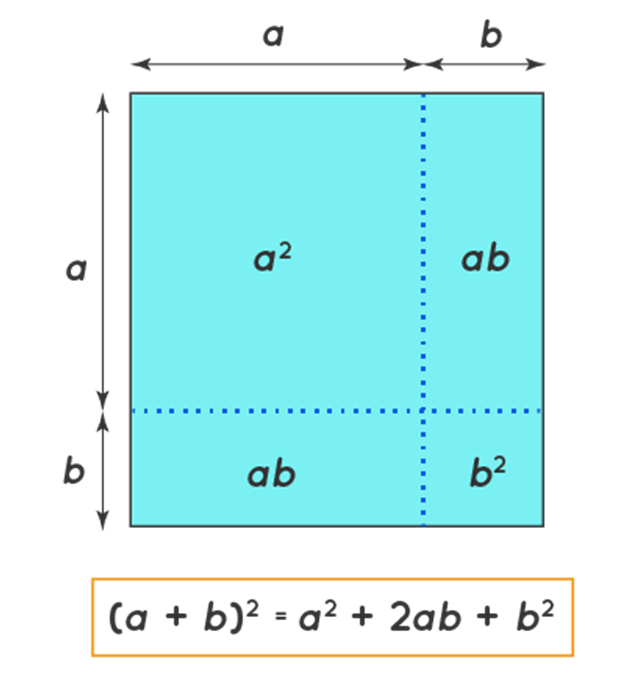
Proof of (a + b)2 = a2 + 2ab + b2
The algebraic expression (a+b)2 is nothing but (a+b) × (a+b). This can be visualized as a square whose sides are (a+b) and the area is (a+b)2. The square with a side of (a + b) can be visualized as four areas of a2, ab, ab, b2. The sum of these areas a2 + ab + ab + b2 gives the area of the square (a+b)2. The area of the square (a+b)2 = a2 + ab + ab + b2 proves the algebraic identity.
Proof of (a + b)(a - b) = a2 - b2
The objective is to find the value a2 - b2, which can be taken as the difference of the area of two squares of sides a units and b units respectively. This is equal to the sum of are areas of two rectangles as presented in the below figure. One rectangle has a length of a units and a breadth of (a - b) units. Another rectangle is taken with a length of (a - b) and a breadth of b units. Further, we take the areas of the two rectangles and sum the areas to obtain the resultant values. The respective areas of the two rectangles are (a - b) × a = a(a - b) , and (a - b) × b = b(a - b). Finally, we take the sum of these areas to obtain the resultant expression.
a(a + b) + b(a - b) = (a + b)(a - b)
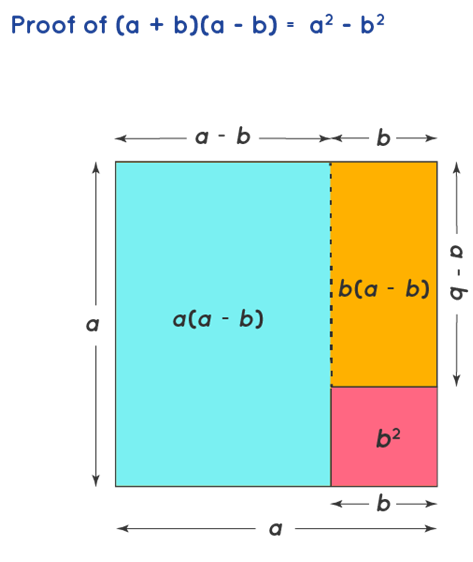
Re-arranging the individual squares and rectangles, we get:
(a+b)(a−b)=a2−b2
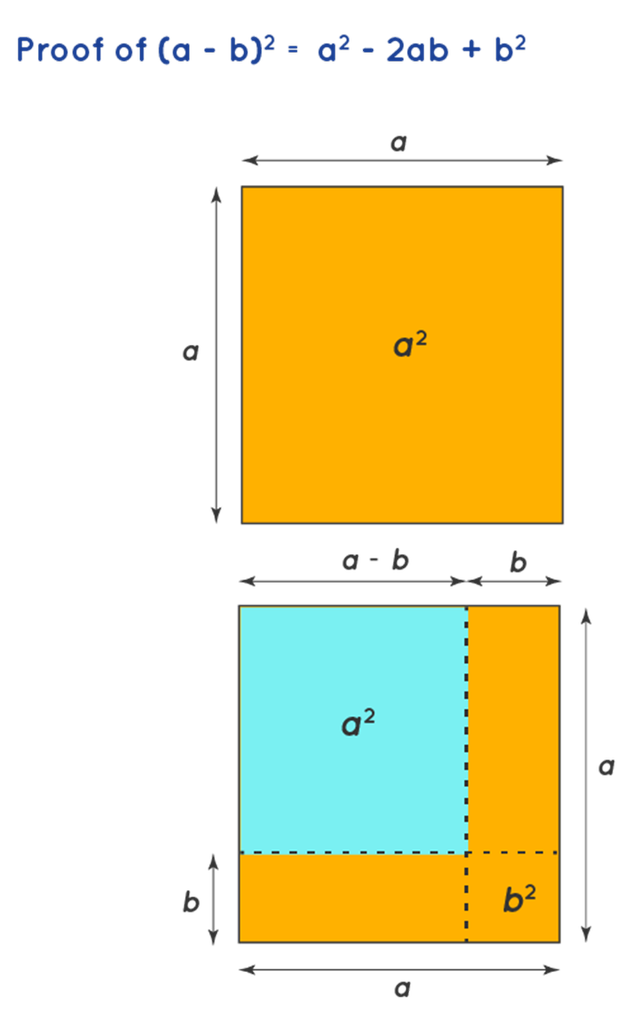
Proof of (a − b)2 = a2 −2 ab + b2
Once again, let’s think of (a - b)2 as the area of a square with length (a - b). To understand this, let's begin with a large square of area a2. We need to reduce the length of all sides by b, and it becomes a - b. We now have to remove the extra bits from a2 to be left with (a - b)2. In the figure below, (a - b)2 is shown by the blue area. To get the blue square from the larger orange square, we have to subtract the vertical and horizontal strips that have the area ab. However, removing ab twice will also remove the overlapping square at the bottom right corner twice. Hence, we add b2. Thus we have (a − b)2 = a2 − ab − ab + b2. Hence this proves the algebraic identity (a − b)2 = a2 − 2ab + b2
Algebraic Identities
Algebraic Identities
Algebraic identities are an important set of formulas in math. They form the foundation working principle of algebra and are helpful to perform computations in simple and easy steps. Certain algebraic problems require working across numerous mathematical step to obtain the answer. Here, with the use of algebraic identities, we are able to perform the calculations without any additional steps. Many of the algebraic identities have been obtained from the binomial expansion of terms.
An algebra identity means that the left-hand side of the equation is identically equal to the right-hand side, for all values of the variables. Here we shall try to acquaint ourselves with all the algebraic identities, their proofs, and how to use these identities in our math calculations.
What Are Algebraic Identities?
Algebraic identities are equations where the value of the left-hand side of the equation is identically equal to the value of the right-hand side of the equation. Unlike algebraic expressions, algebraic identities satisfy all the values of the variables. Let us consider an example to understand this better. Consider the equations: 5x - 3 = 12, 10x - 6 = 24, and x2 + 5x + 6 = 0. These equations satisfy only a unit value and do not work for any other values of the variables. Now let us consider an equation x2 - 9 = (x + 3)(x - 3). These equations satisfy any values of x.
From this, we can clearly understand that an algebra identity has an expression that satisfies any values for the variables. The basic algebraic identities are primarily helpful to work out the numerous math problems. The four basic algebraic identities are as follows.
- (a + b)2 = a2 + 2ab + b2
- (a - b)2 = a2 - 2ab + b2
- (a + b)(a - b) = a2 - b2
- (x + a)(x + b) = x2 + x(a + b) + ab
Algebraic Identities from Binomial Expansion Formula
IThe binomial expansion based on the binomial theorem is helpful to find derive all the algebraic identities. Let us gain a brief idea of the binomial theorem expansion, which would be helpful to derive algebraic identities of higher degrees. Generally, binomial expansion is used for expansion involving two variables and with n degree. The total number of terms of the binomial expansion is (n + 1) and in the expanded form the power of the variable is reducing, and the power of the second variable is increasing in sequential terms. Each of the terms in the binomial expansion has a coefficient associated with it.
The following algebraic identities have been derived from the binomial expansion for sum and difference of variable and for a maximum power of 3 the algebraic identities have been listed below as formulas. Further algebraic identities of higher degrees and more variables can also be derived using the above binomial expansion formula.
- (a + b)2 = a2 + 2ab + b2
- (a - b)2 = a2 - 2ab + b2
- (a + b)(a - b) = a2 - b2
- (a + b)3 = a3 +3a2b + 3ab2 + b3
- (a - b)3 = a3 - 3a2b + 3ab2 - b3
- (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ac
Algebraic Identities for Factorization
Algebraic identities are greatly helpful in easily factorizing algebraic expressions. The given expression representing the expanded form of the formula can be transformed and written as a set of factors using the below algebraic identities. Some of the higher algebraic identities such as a4 - b4 can be easily derived using the basic algebraic identities a2 - b2. The below list presents a set of algebraic identities helpful for the factorization of polynomials.
- a2 - b2 = (a - b)(a + b)
- x2 + x(a + b) + ab = (x + a)(x + b)
- a3 - b3 = (a - b)(a2 + ab + b2)
- a3 + b3 = (a + b)(a2 - ab + b2)
- a4 - b4 = (a - b)(a + b)(a2 + b2)
Algebraic Identities for Three Variables
The algebraic identities for three variables also has been derived using the binomial expansion formula. Further these identities are helpful to easily work across the algebraic expressions with the least number of steps.
- a2 + b2 + c2 = (a + b + c)2 - 2(ab + bc + ac)
- a3 + b3 + c3 - 3abc = (a + b + c)(a2 + b2 + c2 - ab - ca - bc)
- (a + b)(a + c)(b + c) = (a + b + c)(ab + ac + bc) - 3abc
Apart from these simple algebraic identities listed above, there are other algebraic identities that we will use in higher grades.
Check them on the page Algebraic Identities Formula and Examples.
Proof of Algebraic Identities
The following proofs of algebraic identities will help us to visually understand each of the identities and better understand it. Let us look at the proofs of each of the basic algebraic identities.
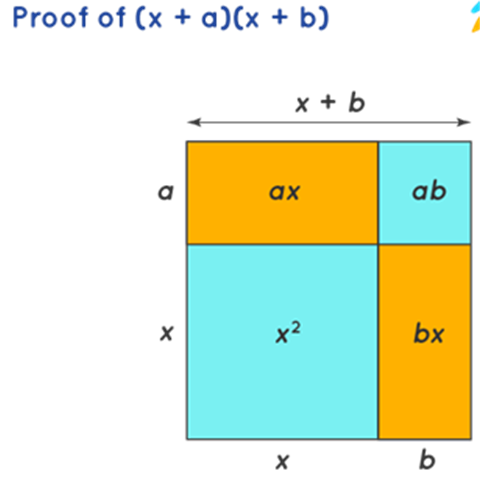
Proof of (x + a)(x + b) = x2 + x(a + b) + ab
(x+a)(x+b) is nothing but the area of a rectangle whose sides are (x+a) and (x+b) respectively. The area of a rectangle with sides (x+a) and (x+b) in terms of the individual areas of the rectangles and the square is x2, ax, bx , ab. Summing all these areas we have x2 + ax + bx + ab. This gives us the proof for the algebra identity (x + a)(x + b) = x2 + ax + bx + ab = x2 + x(a + b) + ab.
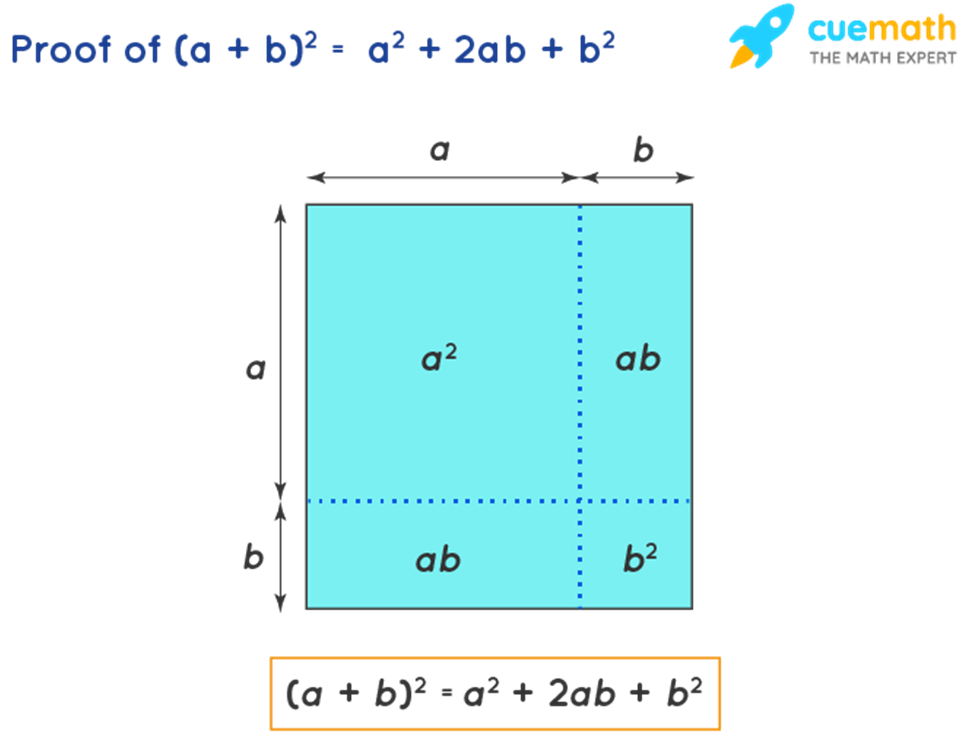
Proof of (a + b)2 = a2 + 2ab + b2
The algebraic expression (a+b)2 is nothing but (a+b) × (a+b). This can be visualized as a square whose sides are (a+b) and the area is (a+b)2. The square with a side of (a + b) can be visualized as four areas of a2, ab, ab, b2. The sum of these areas a2 + ab + ab + b2 gives the area of the square (a+b)2. The area of the square (a+b)2 = a2 + ab + ab + b2 proves the algebraic identity.
Proof of (a + b)(a - b) = a2 - b2
The objective is to find the value a2 - b2, which can be taken as the difference of the area of two squares of sides a units and b units respectively. This is equal to the sum of are areas of two rectangles as presented in the below figure. One rectangle has a length of a units and a breadth of (a - b) units. Another rectangle is taken with a length of (a - b) and a breadth of b units. Further, we take the areas of the two rectangles and sum the areas to obtain the resultant values. The respective areas of the two rectangles are (a - b) × a = a(a - b) , and (a - b) × b = b(a - b). Finally, we take the sum of these areas to obtain the resultant expression.
a(a + b) + b(a - b) = (a + b)(a - b)
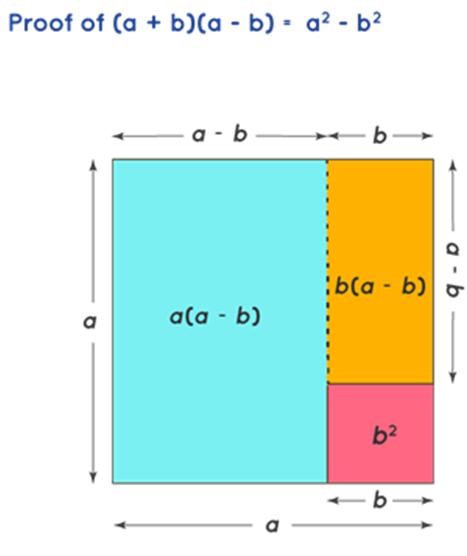
Re-arranging the individual squares and rectangles, we get:
(a+b)(a−b)=a2−b2
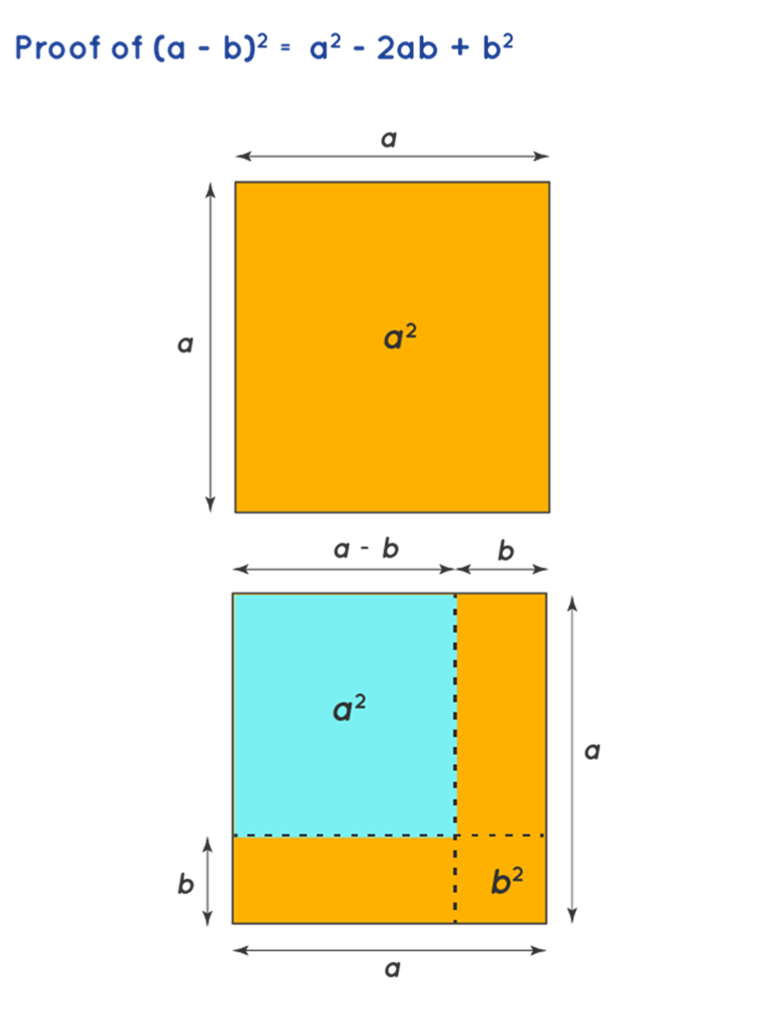
Proof of (a − b)2 = a2 −2 ab + b2
Once again, let’s think of (a - b)2 as the area of a square with length (a - b). To understand this, let's begin with a large square of area a2. We need to reduce the length of all sides by b, and it becomes a - b. We now have to remove the extra bits from a2 to be left with (a - b)2. In the figure below, (a - b)2 is shown by the blue area. To get the blue square from the larger orange square, we have to subtract the vertical and horizontal strips that have the area ab. However, removing ab twice will also remove the overlapping square at the bottom right corner twice. Hence, we add b2. Thus we have (a − b)2 = a2 − ab − ab + b2. Hence this proves the algebraic identity (a − b)2 = a2 − 2ab + b2

 ABCD CLASSES
ABCD CLASSES
