- Books Name
- CBSE Class 6 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 6
- Subject
- Mathmatics
Some problems on HCF and LCM
Ex. Find the greatest number which divides 43 and 91 leaving remainder 7 in each caes.
Sol. It is given that the required number when divides 43 and 91, the renainder is 7 in each case . This means that 43 – 7 = 36 and 91– 7 = 84 are completely divisible by required number .
Also, the required number is the greatest number satisfying the above property .
∴ It is the HCF of 36 and 84.
36 = 2 × 2 × 3 × 3
84 = 2 × 2 × 3 × 7
∴ Required HCF = 2 × 2 × 3 = 12
Hence, the required number = 12
Ex. Find the largest number that will divide 20, 57 and 85 leaving remainders 2, 3 and 4 respecitively.
Sol. Clearly, the required number is the HCF of the number 20 – 2 = 18, 57 – 3 = 54 and 85 – 4 = 81.
18 = 2 × 3 × 3
54 = 2 × 3 × 3 × 3
81 = 3 × 3 × 3 × 3
∴ Required HCF = 3 × 3 = 9
Hence, the required number = 9
Relationship between HCF and LCM
Let us take two numbers, say 16 and 24.
The HCFof 16 and 24 is 8.
The LCM of 16 and 24 is 48.
Since 8 is factor of 48, so we can say that HCF of the numbers is a factor of their LCM.
Product of HCF and LCM = 8 × 48 = 384
Product of Numbers = 16 x 24 = 384
So we can say that the product of two numbers is equal to the product of their HCF and LCM.
Let a and b are two numbers then
a x b = HCF × LCM
Ex. The HCF of two number is 29 and their LCM is 1160. If one of the number is 145, find the other.
Sol. We know that
Product of the number = HCF × LCM
x × 145 = 29 × 1160
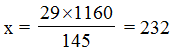
∴ Required number = 232
Ex. Find the least number which when divided by 6, 7, 8, 9 and 10 leaves reamainder 1.
Sol. As the remainder is same
Required number = LCM of divisors + Remainder
= LCM (6, 7, 8, 9, 10) +1
= 2520 + 1 = 2521
Ex. Find the least number which when decreased by 7 is exactly divisible by 12, 16, 18, 21 and 28.
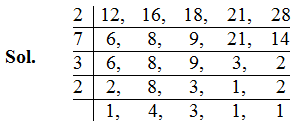
LCM = 2 × 7 × 3 × 2 × 4 × 3 = 1008
Required number = 1008 + 7 = 1015.

 ReginaTagebücher
ReginaTagebücher
 Param Publication
Param Publication
