- Books Name
- CBSE Class 6 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 6
- Subject
- Mathmatics
Representation of integers on a number line
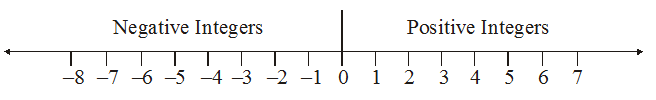
First we draw a line and mark some points at equal distance on it as shown in the figure. Mark a point as zero on it. Points to the right of zero are positive integers and are marked + 1, + 2, + 3, etc. or simply 1, 2, 3 etc. Points to the left of zero are negative integers and are marked – 1, – 2, – 3 etc.
In order to mark – 6 on this line, we move 6 points to the left of zero.
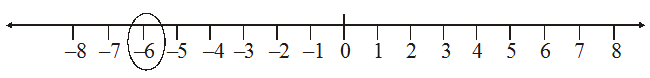
In order to mark + 2 on the number line, we move 2 points to the right of zero.
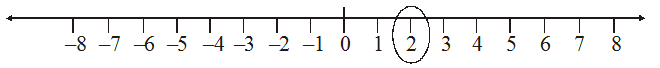
Ordering of integers
Let we observe the integers which are represented on the number line.
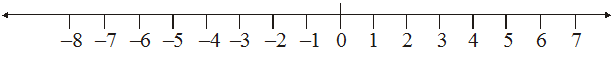
We know that 7 > 4 and from the number line shown above, we observe that 7 is to the right of 4.
Similarly, 4 > 0 and 4 is to the right of 0. Now, since 0 is to the right of –3 so, 0 > – 3. Again, – 3 is to the right of – 8 so, – 3 > – 8.
Thus, we see that on a number line the number increases as we move to the right and decreases as we move to the left.
Therefore, – 3 < – 2, – 2 < – 1, – 1 < 0, 0 < 1, 1 < 2, 2 < 3 so on.
Hence, the collection of integers can be written as..., –5, –4, – 3, – 2, – 1, 0, 1, 2, 3, 4, 5...
Ex. Write all integers between
(i) – 2 and 3 (ii) – 4 and 2
![]()
(i) The integers between – 2 and 3 are –1, 0, 1, 2.
(ii) The integers between – 4 and 2 are – 3, – 2, –1, 0, 1.

 Param Publication
Param Publication
