2. Quadrilaterals, Polygons and Three Dimensional Shapes

Line Segment
A line segment is a fixed portion of a line. This makes it possible to measure a line segment. This measure of each line segment is a unique number called its “length”. We use this idea to compare line segments.
To compare any two line segments, we find a relation between their lengths.
This can be done in several ways.
(i)     Comparison by observation: The method of comparing two segements by observations is not always correct. Therefore, we need a better method. 
(ii)     Comparison using Ruler and a Divider : 
(a)     Using a Ruler : Suppose we have to measure the length of a given   segment AB. Take a ruler with centimeter marks and place it along the segment AB such that the 

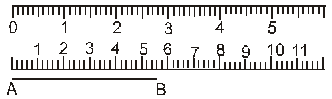
zero mark on the ruler is just at A as shown in the figure. Now read the mark on the ruler which corresponds to B. In this figure we see that the mark corresponding to B is the eighth small division after 5, i.e. AB contains 5 full centimeters and 8 millimeters. We say that the length of AB is 5.8 cm and write it as AB = 5.8 cm. 

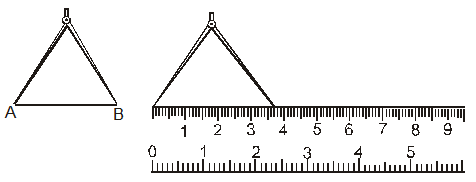
(b)    Using a Divider : We open the divider such that the point of one arm is at A and the second exactly at B, i.e. the segment AB is contained in the divider. Now lift the divider carefully without disturbing its opening and place it on the ruler so that one point of the divider is at zero (0) mark. We then read the mark which corresponds to the second point of the divider. 
In the adjoining figure the second point of the divider is at the seventh mark after 3, 
i.e. AB contains 3 complete centimetres and seven-tenths of a centimetre. We say that AB is 3 cm and 7 mm and write it as AB = 3.7 cm. 

Units for measurment of line segments :The unit of measurment of length is metre.
A metre is divided into 100 equal  parts, each called a centimetre. A centimetre is further subdivided into  10 equal parts, each called a millimetre.    
Thus we have the following table :
          10 Millimetres (mm) = 1 Centimetre (cm)
          10 Centimetres(cm) = 1 Decimetre (dm)
          10 Decimetres (dm) = 1 Metre (m)
 or ,    1 metre  = 10 decimetres
                        = 100 centimetres 
                        = 1000 millimetres 

Ex.    If B is the mid point of AC and C is the mid-point of BD where A, B, C and D are collinear, show that AB = CD ?

Sol.     B is the mid-point of AC
        ∴     AB = BC                   .....(i)
            Again C is the mid-point of BD
            CD = BC                  .....(ii)            
            From (i) and (ii), we get 
            AB = CD