- Books Name
- CBSE Class 6 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 6
- Subject
- Mathmatics
Construction of Special Angles
Constructing a 60° angle
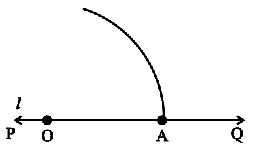
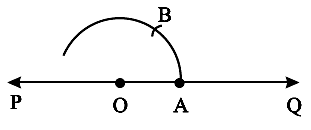
Step 1 Draw a line l and mark a point O on it.
![]()
Step 2 Place the pointer of the compasses at O and draw an arc of convenient radius which cuts the line PQ at a point say, A.
Step 3 With the pointer at A (as centre), now draw an arc that passes through O.
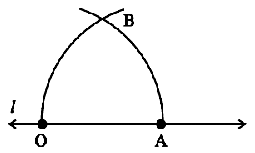
Step 4 Let the two arcs intersect at B. Join OB. We get ∠BOA whose measure is 60°.
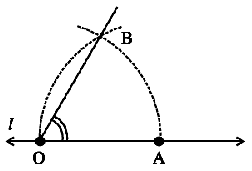
Constructing a 30° angle
Construct an angle of 60° as shown earlier. Now, bisect this angle. Each angle is 30°, verify by using a protractor.
Constructing a 120° angle
An angle of 120° is nothing but twice of an angle of 60°. Therefore, it can be constructed as follows :
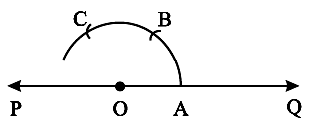
Step 1 Draw any line PQ and take a point O on it.
![]()
Step 2 Place the pointer of the compasses at O and draw an arc of convenient radius which cuts the line at A.
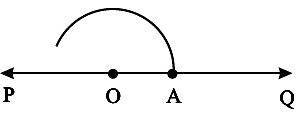
Step 3 Without disturbing the radius on the compasses, draw an arc with A as centre which cuts the first arc at B.
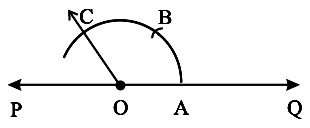
Step 4 Again without disturbing the radius on the compasses and with B as centre, draw an arc which cuts the first arc at C.
Step 5 Join OC, ∠COA is the required angle whose measure is 120°.
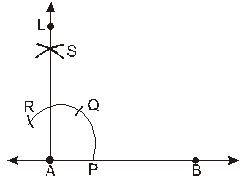
Constructing a 90° angle
Step 1 With A as centre and any suitable radius draw an arc cutting AB at P.
Step 2 With P as centre and the same radius as before cut the arc of Step 1 at Q. With Q as centre and the same radius cut the arc again at R.
Step 3 With Q and R as centres and any convenient radius (same for both) draw arcs cutting at S. Join A to S and produce A to L. Then ∠BAL = 90°, i.e., AL is perpendicular to AB at A.

 Param Publication
Param Publication
