- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
Practical Problems on Union and Intersection(Applications of Sets)
Daily Life Examples Of Sets
- In Kitchen. Kitchen is the most relevant example of sets. ...
- School Bags. ...
- Shopping Malls. ...
- Universe. ...
- Playlist. ...
- Rules. ...
- Representative House. etc…
Cardinality of Finite sets:
If A & B are two finite sets, then the cardinality of A È B is given by
|AÈB| = |A| + |B| - |A Ç B|
Note:
(1) n(AÈB )= |AÈB| = |A| + |B| if A Ç B = f, i.e. A & B are two finite disjoint sets.
(2) n(AÈBÈC)=|AÈBÈC| = |A| + |B| + |C| - |AÇB| - |BÇC| - |CÇA| + |AÇBÇC|
(3) n (A – B) = n (A ∪ B) – n (B)
n (B – A) = n (B) – n (A ∩ B)
(4) n (A ∪ B)′= n (U) – n (A ∪ B) = n (U) – n (A) – n (B) + n (A ∩ B)
(5) n ( A ∪ B )' = n ( U) – n ( A ∪ B)
Order pair:
Let A be a set and a, b Î A, then the order pair of a & b in A denoted by (a, b). Here a is called first co-ordinate & b is called the second co-ordinate.
N.B. In a order pair (a, b), the respective order of the entries is always constant, we can not alter their respective orders. If we do so, it will be an different element.
Cartesian product of two sets:
Definition:
If A and B are two non-empty sets, then their Cartesian product, denoted by A X B is defined to be the set of order pairs as
A X B = {(a, b) | x ÎA, b Î B}
Example: A = {a, b, c}
B = {1, 2, 3}
A X B = {(a, 1), (a, 2), (a,3), (b,1), (b, 2), (b,3), (b,1), (c, 2), (c, 3)}
Note:
(1) A X B ¹ B X A is A ¹ B i.e. Cartesian product is not commutative.
(2) If cardinality of A is n and cardinality of B is n then cardinality of (A X B) is mn.
(3) A X (B Ç C) = (A X B) Ç (A X C)
(4) A X (B ÈC) = (A X B) È (A X C)
Solved examples:
Q.1: Prove that A – B = A Ç B/, where A & B are any two sets.1
Proof: Let x Î A –B be an arbitrary element.
Û x Î& x Ï B
Û x Î A & x Î B/
Û x Î AÇB/
\ A – B Ì A Ç B/ ----------- (1)
And A Ç B/ Ì A – B ----------- (2)
From 1 & 2 we have,
A – B = A Ç B/
Q.2: Prove that A È B = B È A, where A & B are any two sets.
Proof: Let x Î A È B be an arbitrary element.
Now x Î A È B
Û x Î A or x Î B
Û x Î B or x Î A
Û x Î B È A
\ A È B Í B È A -------------- (i)
And B È A Í A È B --------------- (ii)
From (i) & (ii), we have
A È B = B È A
Q.3: Prove that A È (B Ç C) =(AÈB) Ç (A È C), for any three sets A, B & C.
Proof. Let x Î A È (B ÇC) be an arbitrary element.
Now x Î A È (B Ç C)
Û x Î A or x Î (B Ç C)
Û x Î A or (x Î B and x Î C)
Û (x Î A or x Î B) and x Î A or x Î C)
Û x Î A È B and x Î A È C
Û x Î (A È B) Ç (A È C)
\ A È (BÇC) Í (A È B) Ç (A È c) -------------- (i)
And (A È B) Ç (A È C) = A È (B Ç C) -------------- (ii)
From (i) and (ii) we have
A È (BÇC) = (A È B) Ç (A È c)
Q.4: Prove that A – (A – B) Í B for any two set A & B.
Proof: Let x Î A – (A –B) be arbitrary.
Þ x Î A and x Ï (A – B)
Þ x Î A and (x Ï A and x Î B)
Þ x Î B
Þ A – (A – B) Í B
Q.5: For any three sets A, B and C, prove that A Ç (B Ç C) = (A Ç B) Ç C
Proof: Let x Î A Ç (B Ç C) be an arbitrary element.
Now x Î A Ç (B Ç C)
Û x Î A and x Î (B Ç C)
Û x Î A and (x Î B and x Î C)
Û (x Î A and x Î B) and x Î C
Û x Î A Ç B) Ç C
\A Ç (B Ç C) Í (A Ç B) Ç C ------------ (1)
And (A Ç B) Ç C Í A Ç (B Ç C) ------------ (2)
From 1 & 2, we have
A Ç (B Ç C) = (A Ç B) Ç C
Q.6: If A D B = B D C, then prove that A = C for any three set A, B and C.
Proof: Given that A D B = B D C
Þ (A È B) – (A Ç B) = (B È C) – (B Ç C)
Þ A ÈB = BÈC and A Ç B = B Ç C
Þ (A ÈB) Ç Bc = (C È B) Ç Bc and A Ç B = B Ç C
Þ (A Ç Bc) È f = (C Ç Bc) È f and A Ç B = B Ç C
Þ (A Ç Bc) = C Ç Bc and A Ç B = B Ç C
Þ A – B = C – B and A Ç B = B Ç C
Þ (A – B) È A Ç B = (C – B) È (B Ç C)
Þ A = C
Q.7: Prove that for any three sets A, B, C
|AÈBÈC| = |A| + |B| + |C| - |A ÇB| - |BÇC| - |CÇA| + |AÇBÇC|
Proof: Let B È C = D
Now |AÈBÈC| = |AÈD|
= |A| + |D| - |A Ç D|
= |A| + |BÈC| - |AÇD|
= |A| + |B| + |C| - |BÇC| - |AÇ(BÈC)|
= |A| + |B| + |C| - |BÇC| - |(AÇB) È (AÇC)|
= |A| + |B| + |C| - |BÇC| - {|AÇB| + |AÇC| - |(AÇB) Ç (AÇC)|}
= |A| + |B| + |C| - |BÇC| - |AÇB|-|AÇC| + |AÇBÇC|
Þ |AÈBÈC| = |A| + |B| + |C| - |AÇB| - |BÇC| - |CÇA| + |AÇBÇC|
Q.8: A company must hire 25 programmers to handle systems programming jobs and 40 programmers for applications programming of those hired, 10 will be expected to perform jobs for both types. How many programmers must be hired?
Ans. A = Set of system programmers hired
B = Set of application programmers hired.
According to the question
|A| = 25, |B| = 40 , |A Ç B| = 10
The number of programmers that must be hired is
|A È B| = |A| + |B| - |A Ç B|
= 20 + 40 – 10 = 55
Hence 55 programmers must be hired.
Q.9: In a class of 35 students, 17 have taken mathematics, 10 have taken mathematics but not economics. Find the number of students who have taken both mathematics and economics and the number of students who have taken economics but not mathematics. If it is given that each student can have either mathematics or economic or both.
Ans. Let
A = Set of students who have taken mathematics.
B = Set of students who have taken economics.
Hence as per question,
|A È B| = 35
|A| = 17
|A – B| = 10
Now |(A)| = |A – B| + |A Ç B|
Þ 17 = 10 + |A Ç B|
Þ |A Ç B| = 7
Hence 7 students have taken both mathematics and economics.
Now |A ÈB| = |A| + |B| - |A Ç B|
Þ 35 = 17 + |B| - 7
Þ |B| = 35 – 10
= 25
Now |B| = |B – A| + |A Ç B|
Þ 25 = |B – A| + 7
Þ |B – A| = 25 – 7
= 18
Hence 18 students have taken economics but not mathematics.
Q.10: In a class, 38 students play football. 15 play basketball, 20 play cricket.
In a survey of 60 readers, it was found that 25 read Times of India, 26 read The Hindu, 26 read Indian Express, 9 read both Times of India and The Hindu, 11 both Times of India and Indian Express, 8 read The Hindu and Indian Express and 3 read all the three News Papers. Find the number of readers who read at least one of the three News Papers and also find the no. of people who read only Times of India.
Ans: Let T = Set of readers who read Times of India.
H = Set of readers who read The Hindu.
E = Set of people who read Indian Express.
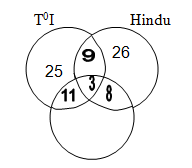
According to the question
|T| = 25
|H| = 26
|E| = 26
|TÇ H| = 9
|TÇE| = 11, |H Ç E| = 8
& |TÇHÇE| = 3
Now |TÈ H È E| = |T| + |H| + |E| - |TÇH| - |HÇE| - |EÇT| + |TÇHÇE|
= 25 + 26 + 26 – 9 -11 – 8 + 3 = 52
Thus the number of readers who read at least one, of the three news paper is 52.
Now the number of readers who read only Times of
= |T| - |TÇH| - |TÇS| + |TÇHÇE|
= 25 – 9 -11 + 3 = 8
Hence 8 readers read only Times of India.
Q.11: If A = {1, 2, 3} B = {4, 5, 6}. Find A X B & B X A
Ans: A = {1, 2, 3}
B = {4, 5, 6}
A X B = {(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6)}
B X A = {(4, 1), (4, 2), (4, 3), (5, 1), (5, 2), (5, 3), (6, 1), (6, 2), (6, 3)}
Q.12: Prove that for any three sets A, B, C A X (BÇC) = (A X B) Ç (A X C)
Proof: Let (x, y) Î A x (B Ç c) be an arbitrary order pair.
(x, y) Î A X (B Ç C)
Û x ÎA and y Î (B Ç C)
Û x ÎA and (y Î B, y Î C)
Û (x ÎA ,y ÎB) and (x Î A, y Î C)
Û (x, y) Î (A X B) and (x, y) Î (A X C)
Û (x, y) Î (A X B) and (x, y) Î (A X C)
Û (x, y) Î (A X B) Ç (A X C)
\ A X (BÇC) Í (A X B) Ç (A X C) ------------------- (i)
And (A X B) Ç (A X C) Í A X (B Ç C) ------------------- (ii)
From (i) and (ii) we have
A X (BÇC) = (A X B) Ç (A X C)
Q.13: Prove that A X (B – C) = (A X B) – (A X C) for any three sets A, B & C
Proof: Let (x, y) Î A X (B – C) be arbitrary (x, y) Î A X (B – C)
Û x Î A , y Î (B – C)
Û x Î A ,(y ÎB and y Ï C)
Û x Î A and y Î B) and (x Î A but y Ï C)
Û (x, y) Î A X B and (x, y) Ï A X C
Û (x, y) Î (A X B) – (A X C)
\ A X (B – C) Í (A X B) – (A X C) --------------- (1)
And (A X B) – (A X C) Í A X (B – C) --------------- (2)
From 1 and 2, we have,
A X (B – C) = (A X B) – (A X C)

 KRISHNA PUBLICATIONS
KRISHNA PUBLICATIONS
