- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics
Construction of a Tangent to a Circle at a given point when its centre is not known :
Steps of construction :
Draw a circle of radius r cm.
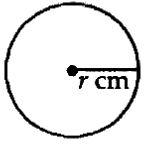
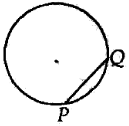
Mark a point P on it. Draw any chord PQ.
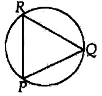
Take a point R on the major arc QP. Join RP & RQ.
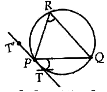
Produce TP to T" such that T' PT is the required tangent at P.
Construction of Tangent to a Circle from a Point Outside it when the Centre of the Circle is
known :
Steps of Construction :
Draw a circle with O as centre and radius r cm. Mark a point P outside the circle such that OP = x cm.
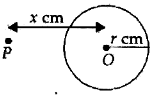
Join OP and draw its perpendicular bisector, which cut OP at M.
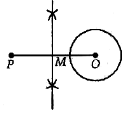
Steps of Construction :
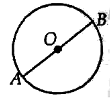
Draw a circle with O as centre and radius r cm and any diameter AOB of this circle.
Construct the given angle at O such that radius OC meets the circle at C. (Suppose given angle is 90º)
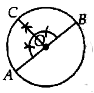
Draw perpendicular at A and C intersect each other at P.
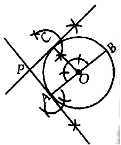
Hence PA and PC are the required tangents to the given circle, inclined at a given angle.

 Param Publication
Param Publication
