Division of a line segment in a given ratio (internally)
- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics
INTRODUCTION
In previous classes, we have studided certain constructions using a ruler and a compass. There are : bisecting an angle, drawing the perpendicular bisector of a line segment, construction of some triangle, etc. We have also given their justifications. Here, we shall study some more constructions taking into use the above pervious knowledge. Also, we shall give mathematical reasoning underlying these constructions.
Divison of A line segment :
In order to divide a line segment internally in a given ratio m : n, where both m and n are positive integers, we follow the following steps :
Steps of construction :
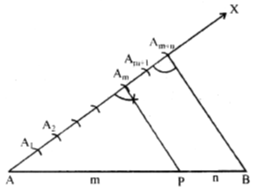
(i) Draw a line segment AB of given length by using a ruler.
(ii) Draw any ray AX making a suitable acute angle with AB.
(iii) Along AX draw (m + n) arcs intersecting the rays AX at A1, A2 ............, Am, Am+1, ........., Am + n such that AA1 = A1A2 =...............= Am+n–1 Am+n
(iv) Join B Am+n
(v) Through the point Am draw a line parallel to Am+n B by making ∠AAm P = ∠AAm+n B.
Suppose this line meets AB at point P.
The point P so obtained is the required point which divides AB internally in the ratio m : n.
Illustration
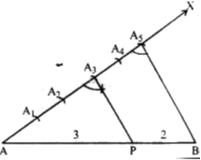
Divide a line segment of length 12 cm internally in the ratio 3 : 2.
Solution
Steps of construction :
(i) Draw a line segment AB = 12 cm by using a ruler.
(ii) Draw a ray making a suitable acute angle ∠BAX with AB.
(iii) Along AX, draw 5 ( = 3 + 2) arcs intersecting the rays AX at A1, A2, A3, A4 and A5 such that
AA1 = A1A2 = A2A3 = A3A4 = A4A5
Tangent to a circle from a point outside it?
- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics
Construction of a Tangent to a Circle at a given point when its centre is not known :
Steps of construction :
Draw a circle of radius r cm.
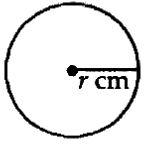
Mark a point P on it. Draw any chord PQ.
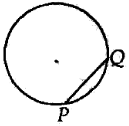
Take a point R on the major arc QP. Join RP & RQ.
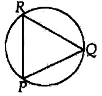
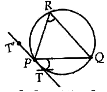
Produce TP to T" such that T' PT is the required tangent at P.
Construction of Tangent to a Circle from a Point Outside it when the Centre of the Circle is
known :
Steps of Construction :
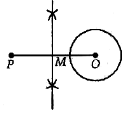
Draw a circle with O as centre and radius r cm. Mark a point P outside the circle such that OP = x cm.
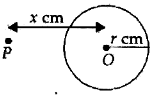
Join OP and draw its perpendicular bisector, which cut OP at M.
Steps of Construction :
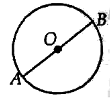
Draw a circle with O as centre and radius r cm and any diameter AOB of this circle.
Construct the given angle at O such that radius OC meets the circle at C. (Suppose given angle is 90º)
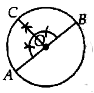
Draw perpendicular at A and C intersect each other at P.
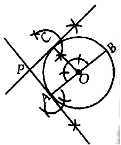
Hence PA and PC are the required tangents to the given circle, inclined at a given angle.
Construction of a triangle similar to a given triangle?
- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics
Constructions of A triangle similar to a given triangle :
Scale factor :
The ratio m : n of the side of the triangle to be constructed with the corresponding sides of the given triangle is known as their scale factor.
(I) Steps of construction when m < n :
(i) Construct the given triangle ABC by using the given data.
(ii) Take any one of the three side of the given triangle as base. Let AB be the base of the given triangle.
(iii) At one end, say A, of the base AB below the base AB, draw a ray AX making a suitable acute angle with AB below the base AB.
(iv) Along AX mark n point A1, A2, A3, ............, An such that
AA1 = A1A2 = ..............An–1An.
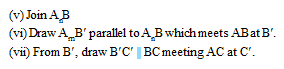
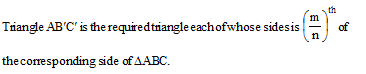
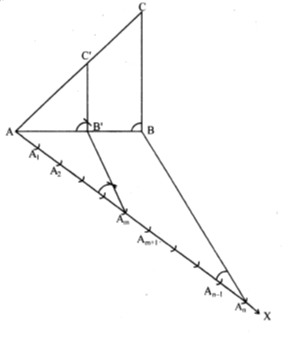
Illustration 1
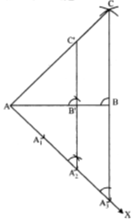
Construct a ∆ABC in which AB = 5 cm, BC = 6 cm and AC = 7 cm. Now, construct a triangle similar to ∆ABC such that each of its sides is two-third of the corresponding sides of ∆ABC.
Solution :
Steps of construction :
(i) Draw a line segment AB = 5 cm.
(ii) With A as centre and radius = 7 cm, draw an arc above AB.
(iii) With B as centre and radius = 6 cm, draw another arc, inter
secting the arc drawn in step (ii) at C.
(iv) Join AC and BC to obtain DABC.
(v) Below AB, draw a ray AX making a suitable acute angle with AB on opposite side of C with respect to AB.
(vi) Draw three arcs (greater of 2 and 3 in 2/3) intersecting the ray AX at A1, A2, A3 such that
AA1 = A1A2 = A2A3


(iv) Draw arcs (large of m and n) intersecting the ray AX at A1, A2, A3 , ..........., Am such that AA1 = A1A2 = ........... = Amm–1 Am.
(v) Join An to B.
(vi) Draw a line through Am parallel to AnB, intersecting the extended line segment AB at B.
(vii) Draw a line through B¢ parallel to BC intersecting the extended line segment AC at C.
(viii) ∆ABCso obtained is the required triangle.

 Param Publication
Param Publication
