- Books Name
- Rakhiedu Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 10
- Subject
- Mathmatics
Constructions of A triangle similar to a given triangle :
Scale factor :
The ratio m : n of the side of the triangle to be constructed with the corresponding sides of the given triangle is known as their scale factor.
(I) Steps of construction when m < n :
(i) Construct the given triangle ABC by using the given data.
(ii) Take any one of the three side of the given triangle as base. Let AB be the base of the given triangle.
(iii) At one end, say A, of the base AB below the base AB, draw a ray AX making a suitable acute angle with AB below the base AB.
(iv) Along AX mark n point A1, A2, A3, ............, An such that
AA1 = A1A2 = ..............An–1An.
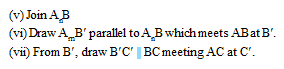
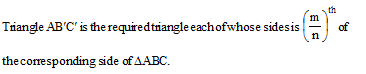
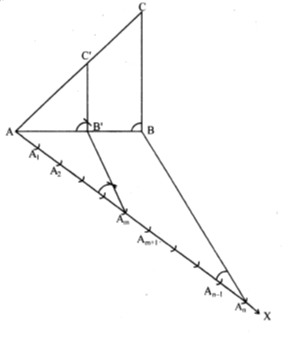
Illustration 1
Construct a ∆ABC in which AB = 5 cm, BC = 6 cm and AC = 7 cm. Now, construct a triangle similar to ∆ABC such that each of its sides is two-third of the corresponding sides of ∆ABC.
Solution :
Steps of construction :
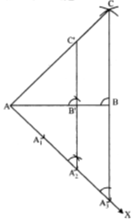
(i) Draw a line segment AB = 5 cm.
(ii) With A as centre and radius = 7 cm, draw an arc above AB.
(iii) With B as centre and radius = 6 cm, draw another arc, inter
secting the arc drawn in step (ii) at C.
(iv) Join AC and BC to obtain DABC.
(v) Below AB, draw a ray AX making a suitable acute angle with AB on opposite side of C with respect to AB.
(vi) Draw three arcs (greater of 2 and 3 in 2/3) intersecting the ray AX at A1, A2, A3 such that
AA1 = A1A2 = A2A3


(iv) Draw arcs (large of m and n) intersecting the ray AX at A1, A2, A3 , ..........., Am such that AA1 = A1A2 = ........... = Amm–1 Am.
(v) Join An to B.
(vi) Draw a line through Am parallel to AnB, intersecting the extended line segment AB at B.
(vii) Draw a line through B¢ parallel to BC intersecting the extended line segment AC at C.
(viii) ∆ABCso obtained is the required triangle.

 Param Publication
Param Publication
