Work Power Energy

WORK DONE

(i) By Constant force

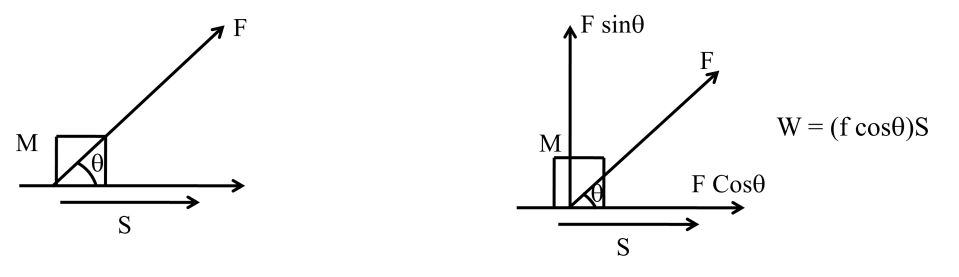
W = (f cosq) S

Work done by constant force = (force). (Displacement in direction of force

                                                = (displacement). (force in direction of displacement)

W=F.S

W = FS Cos

 

Here W is Scalar but it may be +, ─, and zero

Work done will be equal to zero if

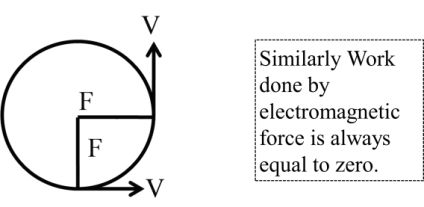
(i) Cosq = 0 = q = 90^o = F ^ S or F ^ V

Ex. Work done by centripetal or centrifugal force is always zero.

Fm=q (V×B)  

 Fm⊥V, Fm⊥B

(2) Displacement = 0, S = 0  in circular motion

Negative work done

If cosq  → negative, 180^o ³ q ³ 90^o

W → ─

Note: Work done by frictional force may be negative.

Example:- It is given that a particle is moving from initial position (2,3,5) to final position (4,1,2) under the action of constant force F=2i+3jN.    what will be the work done by the constant force. 

S��lution-Initial position r1=2i+3j+5K as given (2,3,5)  

Final position r2=4i+j+2k as given (4,1,2)  

Now S=r2-r1=2i-2j-3k  

F=2i+3j  

Now W=F.S.  

=2i+3j. (2i-2j-3k)  

= 4 -6 + 0.

W = -2j                                                                             Ans

(ii) Work done by variable force

Case I: Applying integration force

W=F.dx=F.dy=F.ds  

or W= F.ds or W=F.ds  

Example:- if a variable force F depends on displacement X as F = (3x² -5) due to this force body displaces from x = 2 mater to x = 5 meter find the work done by this variable force. 

Solution: Given F = 3x² – 5,     displacement from x = 2 meter to x = 5 meter 

W=25fdx=253x2-5dx  

     =3 25x2dx-525dx  

3x3325-5X25   

      =33×53-23-55-2  

      = [125 – 8] – 5 x 3

W = 102 J

Case II: Applying graphical method.

W = F.S   if we have group F vs S then area under the S Curve will give us work done.

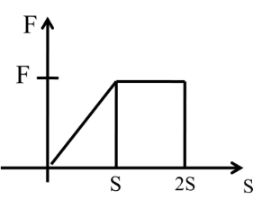Work done = Area under the F – S curve

Area  = 1/2 x basic height + length x width

         = 1/2  x  S  x  F + F x S

      = 3/2 FS

W = 3/2 FS

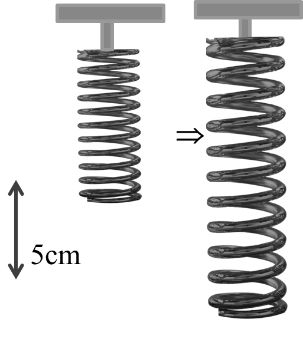Example:- Spring force F = - Kx {Here K is Force constant} it a spring elongate by 5cm and force constant  K is 100N/meter then find work done on stretching the spring.

Solution:

Now F = -K x

            = -100x

W=Fdx  

   =-10000.05xdx  

-100x2200.05  

-10020.052=-50×25×10-4  

= 1205 x 10^-14

W = - 0.125 J                                                      Ans.

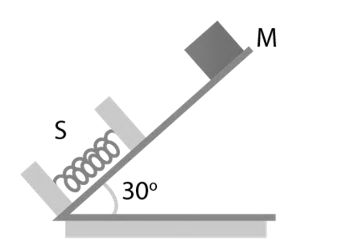Question: An ideal massless spring S can be compressed 1 m by a force of 100 N in equilibrium. The same spring is placed at the bottom of a frictionless inclined at 30° to the horizontal. A 10 kg block M is released from rest at the top of the incline and brought to rest momentarily after compressing the spring by 2 m. If g = 10 ms^-2, what is the speed of mass just before it leave the spring?

a 20 ms-1                                          b 30 ms-1

c10 ms-1                                           d 40 ms-1

Solution: F = kx

∴    k=Fx=1001  

= 100 N/m

E_i = E_f

∴12×10×v2=12×100×22-1010(2sin30°)  

Solving we get,

v=20 m/s                                                                                                       Answer (a)

 

KINETIC ENERGY

Scalar quantity, always will be positive   K = ½ mv²

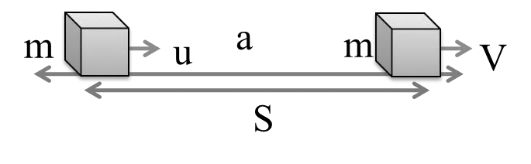Work energy theorem: It is given that a mass is having initial velocity u accelerate and final velocity V and covered a distance S. Here v > u

Initial kinetic energy K1=12mu2  

Final kinetic enrgy=K2=12mv2  

Using equation of motion

v² = u² + 2a s

12m v2-u2=2as12m  

12mv2-12mu2=maS  

K₂-K₁ = FS

ΔK = W

Question: A body of mass m = 10^-2 kg is moving in a medium and experiences a frictional force F = -kv². Its initial speed is v₀ = 10 ms^-1. If after 10s, its energy is 18mv02,  the value of k will be                                                                                                               (2017 JEE Main)

(a) 10^-3 kg^-1                                               (b) 10^-4 kgm^-1

(c) 10^-1 kgm^-1s^-1                                        (d) 10^-3 kgm^-1

Solution: Given, force,   F=kv2

∴Acceleration,a= -kmv2  

or   dvdt= -kmv2  

⇒    dvv2= -km∙dt  

Now, with limits, we have

10vdvv2=-km0tdt     

⇒    -1v10v=-kmt  

⇒  1v=0.1+ktm  

⇒    v=10.1+ktm=10.1+1000k  

⇒ 12×m×v2=18×v02  

⇒v=v02=5  

⇒ 10.1+1000k=5  

Þ    1 = 0.5 + 5000 k

⇒  k=0.55000⇒k=10-4kg/m                                                                Answer (b)

Potential Energy: Scalar quantity may be +, - , Zero 

Here F= -dUdrHere U is potential energy  

F.dr=-dU  

Note: if we find slope (tanq) of u –r graph then we will find amount of force.

 

BY THE U –R GRAPH

Slope at point A is positive

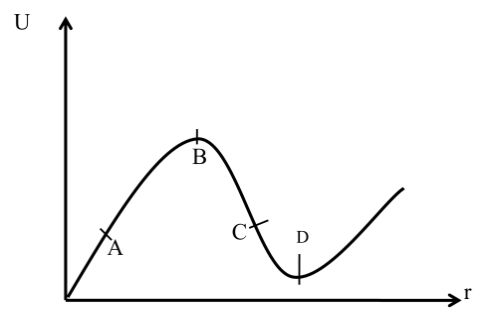Slope at point B is zero here force at B will be zero similarly slope at C is negative slope at point D is zero.

 

 

 

 

 

 

 

TYPES OF POTENTIAL ENERGY

(1) Elastic potential energy: Energy associated with state of Compression or expansion of an elastic object like spring. U = ½ kx²  Here x is the stretch of compression.

(2) Electric Potential energy: Energy associated with state of separation between charged particle

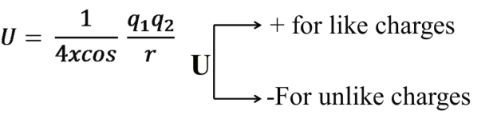
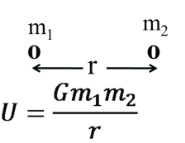(3) Gravitational potential energy

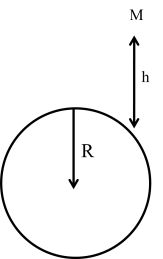U=-Gm1m2r  

Note: Attraction force the An U → negative always

U=mgh1+h/r  

If h <<<<< R

U = mgh                                                                                                                                                                                                         

 

 

Example: A chain is held on a frictionless table with (1/n)th of its length hanging over the edge if the chain has a length L and a mass M. how much work is required to pull the hanging part back on the table.

amgl8n2                                bmgl4n2

cmgl2n2                                dmgln2

Solution:   L length chain mass –M

I length chain mass –M/L

dy length chain mass MLdy  

W = DU

W=Mgl2n2  

du₁ = (dm) gy

du1=MLg0l/nydy  

U1=mLgY220Ln=MLgL22n2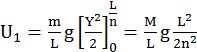  

U1=MgL2n2,  

U₂ = 0 at table

 

CONSERVATIVE AND NON-CONSERVATIVE FORCE

Conservative forces: Work done by conservative forces are independent of path. It only depends on initial and final position.

Ex:- Gravitational forces, electrostatic forces etc.

Note: Work done by conservative forces in closed path is always zero.

W_path1 = W _path2 = W _path3

Non conservative force: Work done by non-conservative forces depends on path.

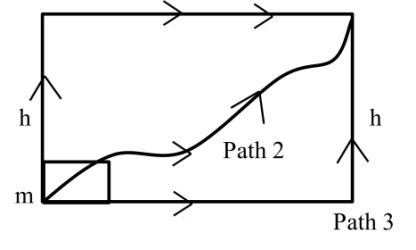Ex:- frictional force, viscous force etc.

Power Work done per unit time P =F.V  

As we know W=∆K=∆U  

P=dwdt=w∆t=dkdt=dudt  

Unit. J/sec or watt

1 horse power = 746 watt.

 

CONSTANT POWER

Case I:- dependency of v on t.

Let an car of mass m accelerates staring from rest, while the engine supplies constant power P then how the V depends on t.

As we know P = Fv

P=mvdvdt  

Pdt=mvdv  

pt=mv22=V2=2ptm  

V=2Ptm=V∝t1/2  

Case II:- dependency of S on t

Let above result V=2ptm  `

dsdt=2Pmt  

0sds=2pmt dt  

S=2Pmt3/23/2   

S= 8P9m1/2 t3/2  

S∝t3/2   

Question: A uniform chain of length pr lies inside a smooth semicircular tube AB of radius r. assuming a slight disturbance to start the chain in motion, the velocity with which it will emerge from the end B of the tube will be

agr1+2π                                          b 2gr2π+π2

c gr  π+2                                         d πgr

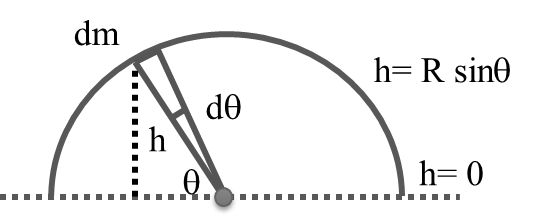Solution: dm=mπ dθ

∴  dU=dmgh= mπdθgrsinθ                 

  Ui= 0πdU=2mgrπ  

Now,  Ki + Ui = Kf + Uf

∴     0+2mgrπ=12mv2-mgπr2  

v=2gr 2π+π2                                                                                                          Answer (b)

 (1) STABLE EQUILIBRIUM

 

 

 

(2) UNSTABLE EQUILIBRIUM

 

 

(3) NEUTRAL EQUILIBRIUM

 

 

 

Question: The given plot shows the variation of U, the potential energy of interaction between two particles with the distance separating them r.

1. B and D are equilibrium points

2. C is a point of stable equilibrium

3. The force of interaction between the two particles is attractive between points C and D and repulsive between D and E

4. The forces of interaction between particles is repulsive between

points E and F.

Which of the above statements are correct?

(a) 1 and 2                                               (b) 1 and 4

(c) 2 and 4                                               (d) 2 and 3

Solution: At C, potential energy is minimum. So, it is stable equilibrium position.

Further,

 

Negative force means attraction and positive force means repulsion.

Question: The potential energy f in joule of particle of mass 1 kg moving in x-y plane obeys the law, f = 3x + 4y. Here, x and y are in metres. If the particle is at rest at (6m, 8m) at time 0, then the work done by conservations force on the particle from the initial position to the instant when it crosses the x-axis is

(a) 25 J                                                    (b) -25 J

(c) 50 J                                                    (d) -50 J

Solution:j

 

Since, particle was initially at rest. So, it will move in the direction of force.

We can see that initial velocity is in the direction of PO. So the particle will cross the X-axis at origin.

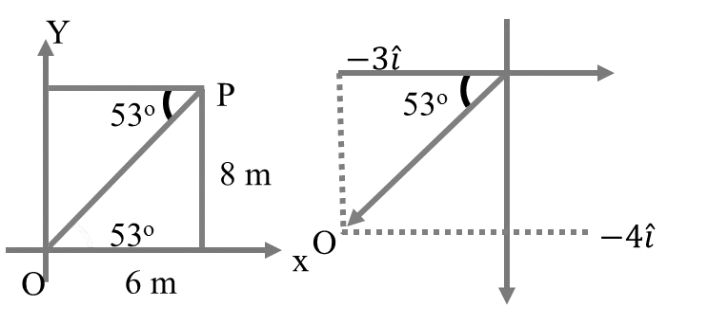
K_i + U_i = K_f + U_f

   0 + ( 3 x 6 + 4 x 8) = K_f + (3 x 0+ 4 x 0)

or    K_f = 50 J                                  Answer (c)