WORK DONE
(i) By Constant force
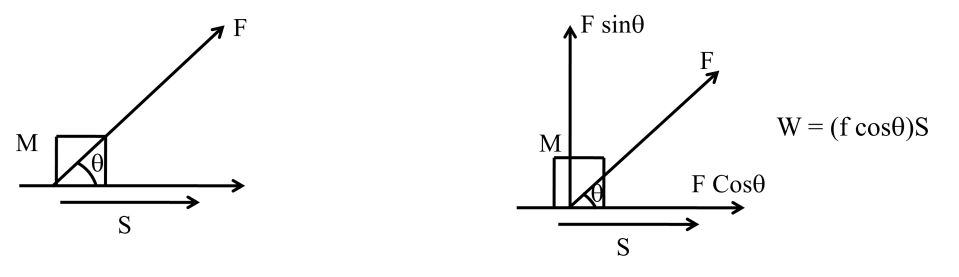
W = (f cosq) S
Work done by constant force = (force). (Displacement in direction of force
= (displacement). (force in direction of displacement)
 W=F.S
W=F.S![]()
W = FS Cos
Here W is Scalar but it may be +, ─, and zero
Work done will be equal to zero if
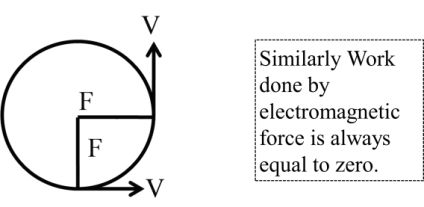
(i) Cosq = 0 = q = 90o = F ^ S or F ^ V
Ex. Work done by centripetal or centrifugal force is always zero.
Fm=q (V×B)![]()
Fm⊥V, Fm⊥B![]()
(2) Displacement = 0, S = 0 in circular motion
Negative work done
If cosq → negative, 180o ³ q ³ 90o
W → ─
Note: Work done by frictional force may be negative.
Example:- It is given that a particle is moving from initial position (2,3,5) to final position (4,1,2) under the action of constant force F=2i+3jN.![]() what will be the work done by the constant force.
what will be the work done by the constant force.
S��lution-Initial position r1=2i+3j+5K as given (2,3,5)![]()
Final position r2=4i+j+2k as given (4,1,2)![]()
Now S=r2-r1=2i-2j-3k![]()
F=2i+3j![]()
Now W=F.S.![]()
=2i+3j. (2i-2j-3k)![]()
= 4 -6 + 0.
W = -2j Ans
(ii) Work done by variable force
Case I: Applying integration force
W=F.dx=F.dy=F.ds![]()
or W= F.ds or W=F.ds![]()
Example:- if a variable force F depends on displacement X as F = (3x2 -5) due to this force body displaces from x = 2 mater to x = 5 meter find the work done by this variable force.
Solution: Given F = 3x2 – 5, displacement from x = 2 meter to x = 5 meter
W=25fdx=253x2-5dx ![]()
=3 25x2dx-525dx![]()
3x3325-5X25![]()
=33×53-23-55-2![]()
= [125 – 8] – 5 x 3
W = 102 J
Case II: Applying graphical method.
W = F.S if we have group F vs S then area under the S Curve will give us work done.
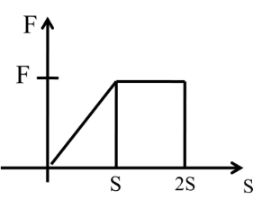 Work done = Area under the F – S curve
Work done = Area under the F – S curve
Area = 1/2 x basic height + length x width
= 1/2 x S x F + F x S
= 3/2 FS
W = 3/2 FS
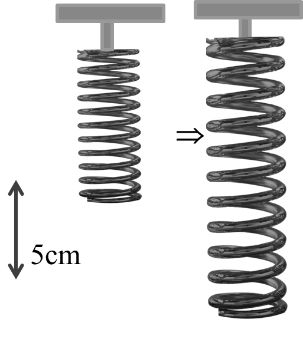 Example:- Spring force F = - Kx {Here K is Force constant} it a spring elongate by 5cm and force constant K is 100N/meter then find work done on stretching the spring.
Example:- Spring force F = - Kx {Here K is Force constant} it a spring elongate by 5cm and force constant K is 100N/meter then find work done on stretching the spring.
Solution:
Now F = -K x
= -100x
W=Fdx ![]()
=-10000.05xdx![]()
-100x2200.05![]()
-10020.052=-50×25×10-4![]()
= 1205 x 10-14
W = - 0.125 J Ans.
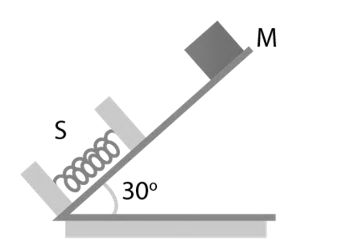 Question: An ideal massless spring S can be compressed 1 m by a force of 100 N in equilibrium. The same spring is placed at the bottom of a frictionless inclined at 30° to the horizontal. A 10 kg block M is released from rest at the top of the incline and brought to rest momentarily after compressing the spring by 2 m. If g = 10 ms-2, what is the speed of mass just before it leave the spring?
Question: An ideal massless spring S can be compressed 1 m by a force of 100 N in equilibrium. The same spring is placed at the bottom of a frictionless inclined at 30° to the horizontal. A 10 kg block M is released from rest at the top of the incline and brought to rest momentarily after compressing the spring by 2 m. If g = 10 ms-2, what is the speed of mass just before it leave the spring?
a 20 ms-1![]() b 30 ms-1
b 30 ms-1![]()
c10 ms-1![]() d 40 ms-1
d 40 ms-1![]()
Solution: F = kx
∴ k=Fx=1001![]()
= 100 N/m
Ei = Ef
∴12×10×v2=12×100×22-1010(2sin30°)![]()
Solving we get,
v=20 m/s![]() Answer (a)
Answer (a)
KINETIC ENERGY
Scalar quantity, always will be positive K = ½ mv2
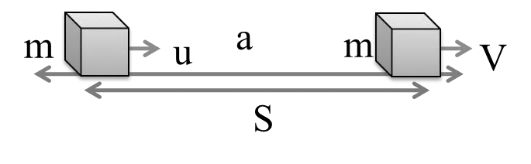 Work energy theorem: It is given that a mass is having initial velocity u accelerate and final velocity V and covered a distance S. Here v > u
Work energy theorem: It is given that a mass is having initial velocity u accelerate and final velocity V and covered a distance S. Here v > u
Initial kinetic energy K1=12mu2![]()
Final kinetic enrgy=K2=12mv2![]()
Using equation of motion
v2 = u2 + 2a s
12m v2-u2=2as12m ![]()
12mv2-12mu2=maS![]()
K2-K1 = FS
ΔK = W
Question: A body of mass m = 10-2 kg is moving in a medium and experiences a frictional force F = -kv2. Its initial speed is v0 = 10 ms-1. If after 10s, its energy is 18mv02,![]() the value of k will be (2017 JEE Main)
the value of k will be (2017 JEE Main)
(a) 10-3 kg-1 (b) 10-4 kgm-1
(c) 10-1 kgm-1s-1 (d) 10-3 kgm-1
Solution: Given, force, F=kv2![]()
∴Acceleration,a= -kmv2![]()
or dvdt= -kmv2![]()
⇒ dvv2= -km∙dt![]()
Now, with limits, we have
10vdvv2=-km0tdt ![]()
⇒ -1v10v=-kmt![]()
⇒ 1v=0.1+ktm![]()
⇒ v=10.1+ktm=10.1+1000k![]()
⇒ 12×m×v2=18×v02![]()
⇒v=v02=5![]()
⇒ 10.1+1000k=5![]()
Þ 1 = 0.5 + 5000 k
⇒ k=0.55000⇒k=10-4kg/m![]() Answer (b)
Answer (b)
Potential Energy: Scalar quantity may be +, - , Zero
Here F= -dUdrHere U is potential energy![]()
F.dr=-dU![]()
Note: if we find slope (tanq) of u –r graph then we will find amount of force.
BY THE U –R GRAPH
Slope at point A is positive
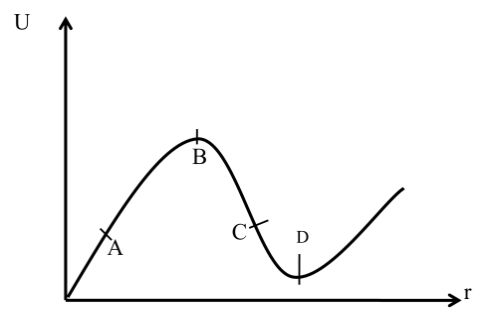 Slope at point B is zero here force at B will be zero similarly slope at C is negative slope at point D is zero.
Slope at point B is zero here force at B will be zero similarly slope at C is negative slope at point D is zero.
TYPES OF POTENTIAL ENERGY
(1) Elastic potential energy: Energy associated with state of Compression or expansion of an elastic object like spring. U = ½ kx2 Here x is the stretch of compression.
(2) Electric Potential energy: Energy associated with state of separation between charged particle
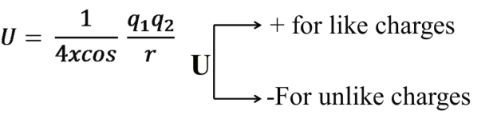
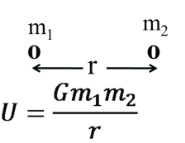 (3) Gravitational potential energy
(3) Gravitational potential energy
 U=-Gm1m2r
U=-Gm1m2r![]()
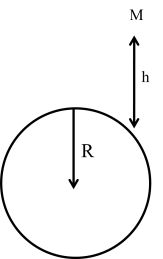
Note: Attraction force the An U → negative always
U=mgh1+h/r![]()
If h <<<<< R
U = mgh
 Example: A chain is held on a frictionless table with (1/n)th of its length hanging over the edge if the chain has a length L and a mass M. how much work is required to pull the hanging part back on the table.
Example: A chain is held on a frictionless table with (1/n)th of its length hanging over the edge if the chain has a length L and a mass M. how much work is required to pull the hanging part back on the table.
amgl8n2![]() bmgl4n2
bmgl4n2![]()
cmgl2n2![]() dmgln2
dmgln2![]()
Solution: L length chain mass –M
I length chain mass –M/L
dy length chain mass MLdy![]()
W = DU
W=Mgl2n2![]()
du1 = (dm) gy
du1=MLg0l/nydy![]()
U1=mLgY220Ln=MLgL22n2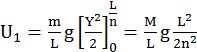
U1=MgL2n2,![]()
U2 = 0 at table
CONSERVATIVE AND NON-CONSERVATIVE FORCE
Conservative forces: Work done by conservative forces are independent of path. It only depends on initial and final position.
Ex:- Gravitational forces, electrostatic forces etc.
Note: Work done by conservative forces in closed path is always zero.
Wpath1 = W path2 = W path3
Non conservative force: Work done by non-conservative forces depends on path.
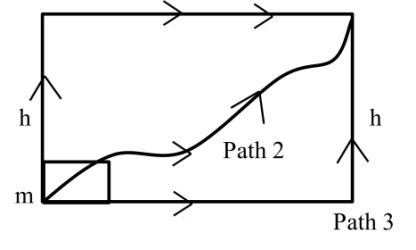 Ex:- frictional force, viscous force etc.
Ex:- frictional force, viscous force etc.
Power Work done per unit time P =F.V![]()
As we know W=∆K=∆U![]()
P=dwdt=w∆t=dkdt=dudt![]()
Unit. J/sec or watt
1 horse power = 746 watt.
CONSTANT POWER
Case I:- dependency of v on t.
Let an car of mass m accelerates staring from rest, while the engine supplies constant power P then how the V depends on t.
As we know P = Fv
P=mvdvdt![]()
Pdt=mvdv![]()
pt=mv22=V2=2ptm![]()
V=2Ptm=V∝t1/2![]()
Case II:- dependency of S on t
Let above result V=2ptm![]() `
`
dsdt=2Pmt![]()
0sds=2pmt dt![]()
S=2Pmt3/23/2 ![]()
S= 8P9m1/2 t3/2![]()
S∝t3/2![]()
Question: A uniform chain of length pr lies inside a smooth semicircular tube AB of radius r. assuming a slight disturbance to start the chain in motion, the velocity with which it will emerge from the end B of the tube will be
agr1+2π![]() b 2gr2π+π2
b 2gr2π+π2![]()
c gr π+2![]() d πgr
d πgr![]()
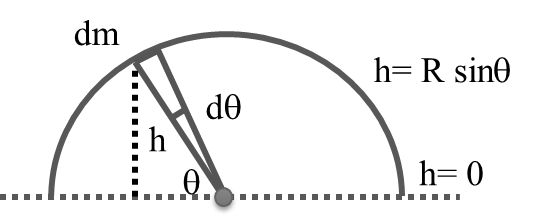 Solution: dm=mπ dθ
Solution: dm=mπ dθ![]()
∴ dU=dmgh= mπdθgrsinθ![]()
Ui= 0πdU=2mgrπ![]()
Now, Ki + Ui = Kf + Uf
∴ 0+2mgrπ=12mv2-mgπr2![]()
v=2gr 2π+π2![]() Answer (b)
Answer (b)

 Kaysons Publication
Kaysons Publication
