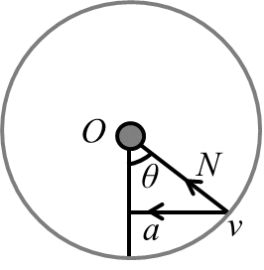
Vertical CM and String Mass

VERTICAL CIRCULAR MOTION

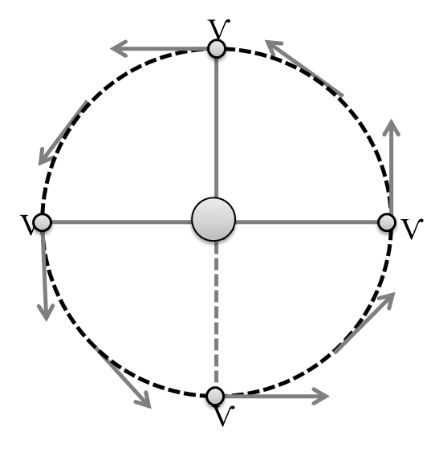
For top point

 

 

For middle position

v² = u² - 2gh

 

 

T_min ≥ 3 mg

VERTICAL CIRCULAR MOTION

For Lowest point

& Lowest to top

v² = u² – 2gh

 

 

 

 

T_min ≥ 6 mg

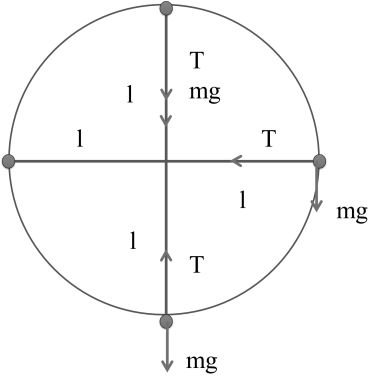
STRING MASS SYSTEM

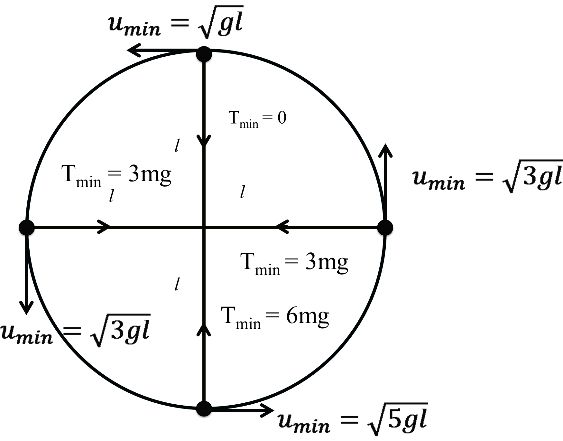
RIM & MASS SYSTEM

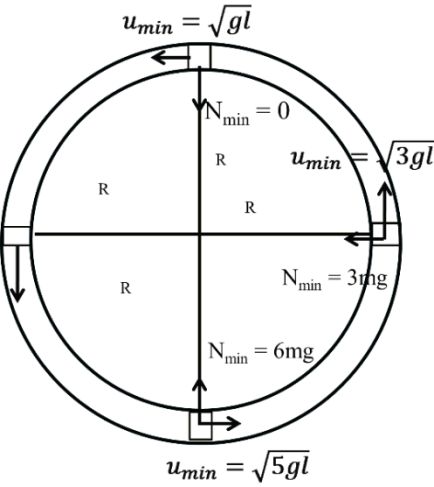
RIGID ROD AND MASS SYSTEM

To Complete the Circle if minimum velocity at top point = 0

 

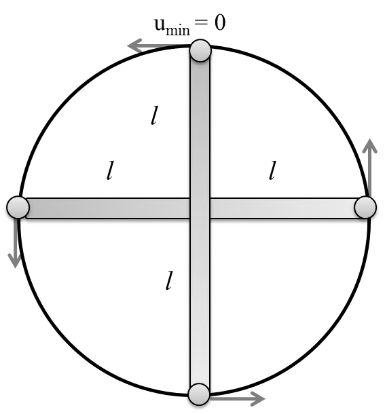
Then Top to bottom

v² = u² - 2gh

(o)² = u² – 2g x 2l

 

At mid point

 

Lowest to mid point

 

v² = u² – 2gh

 

INCOMPLETE CIRCLE

Case I velocity given at lowest position

Case II velocity given at lowest point

 

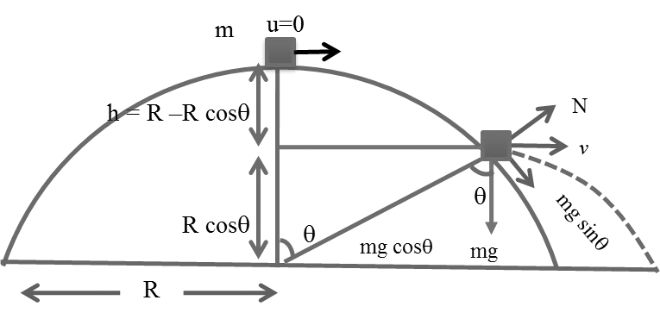
Example: As shown if figure a small mass m is put on the top of smooth hemisphere now this mass slightly hit to disturb it. At what angle it will leave the hemisphere.

      

Leaving the Circle so N = 0

Now from top to point where leave the Circle

v² = u² + 2gh

v² = (0)² + 2gR(1 - cosq)

gR cosq = 2gR (1 - cosq)

Cosq = 2 - 2 cosq

3 cosq = 2

 

 

RADIUS OF CURVATURE

Case I At top of projectile motion

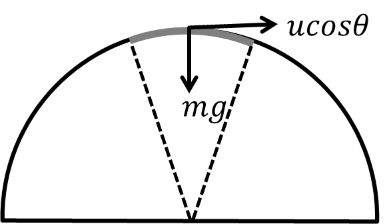
if we assume war the top point of projectile is a small Circular part then

 

 

Case II At any point before the top of projectile

At a point where velocity makes angle q/2 with horizontal

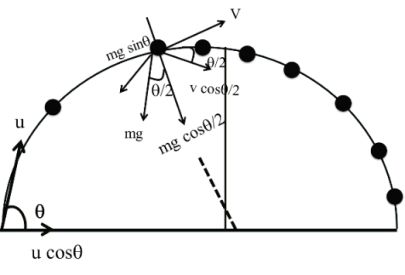
V cosq/2 = u cosq

 

 

 

 

Condition of toppling of a vehicle on circular tracks

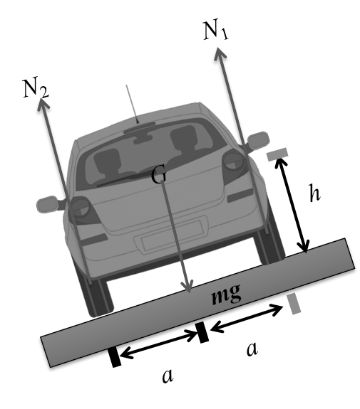
While moving in a circular track normal reaction on the outer wheels

(N₁) is more than the normal reaction on inner wheels (N₂).

Or                   N₁ > N₂

This can be proved as below.

Distance between two wheels = 2a

Height of centre of gravity of car from road = h

For translational equilibrium of car

N₁ + N₂ = mg                      … (i)

 

and for rotational equilibrium of car, net torque about centre of gravity should be zero.

Or                                              N₁ (a) = N₂ (a) + f (h)          … (iii)

From Eq. (iii), we can see that

 

Or                                        N₂ < N₁

From Eq. (iv), we see that N₂ decreases as v is increased.

In critical case,              N₂ = 0

and                          N₁ = mg                          [From Eq. (i)]

                              N₁ (a) = f (h)                   [From Eq. (iii)]

 

 

Therefore, for a safe turn without toppling

From the above discussion, we can conclude while taking a turn on a level road there are two critical speeds, one is the maximum speed for sliding    and another is maximum speed for toppling .   One should keep ones car’s speed less than both for neither to slide nor to overturn.

Case I

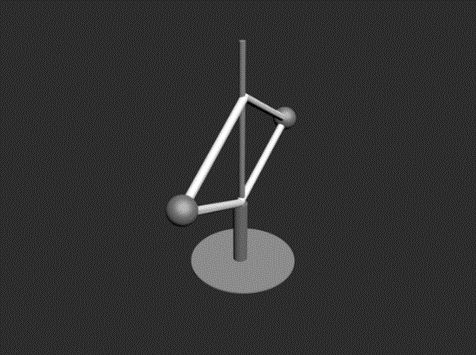
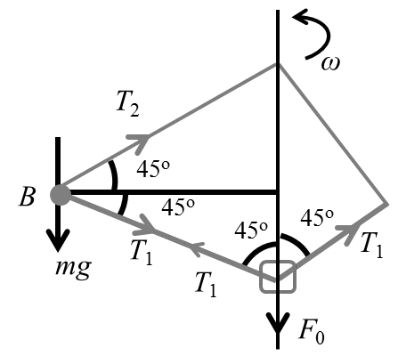
The length of each light rod is l. The mass of each small ball B and D is m. Balls are connected with a light smooth sleeve at point A as shown in the figure below. The frame is rotating with constant angular velocity w. A force F₀ is

Question. If tension in AB wire is T₁ and that in wire BC is T₂. Then the value of (T₂ – T₁) is

(a) mg                                                      

(c) 2 mg                                                    dmg2

Solution: At the ball B,

T₂ sin 45° = mg + T₁ sin 45°           (in vertical direction)

T2-T1=mgsin45°=2 mg         …(i)  

Question. The required force F₀ on the sleeve is

                               

(c) 2 mg                                        

Solution: T₁ cos 45° + T₂ cos 45° = mrw²         (in horizontal direction)

 

or            T₁ + T₂ = mlw²            …(ii)

From Eqs. (i) and (ii), we get        

 

For bead, 2T₁ cos 45° = F₀

                                Answer (a)

Case II

A spherical ball of mass m is kept at the highest point in the space between two fixed, concentric spheres A and B (sec fig.) The smaller sphere A has a radius R and the space between the two spheres has a width d. The ball has a diameter very slightly less than d. All surfaces are frictionless. The ball is given a gentle push (towards the right in the figure). The angle made by the radius vector of the ball with the upward vertical is denoted byq.                                                                                                                                    (2002 JEE Advance)

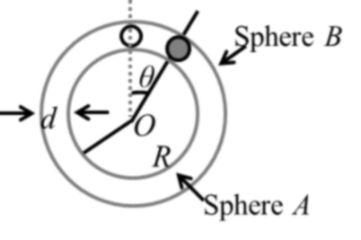
(a) Express the total normal reaction force exerted by the spheres on the ball as a function of angleq.

(b) Let N_A and N_B denote the magnitudes of the normal reaction forces on the ball exerted by the spheres A and B, respectively. Sketch the variations of N_A and N_B as function of cos q in the range 0 £ q £ p by drawing two separate graphs in your answer book, taking cos q on the horizontal axis.

Solution:

Velocity of ball at angle q is

 

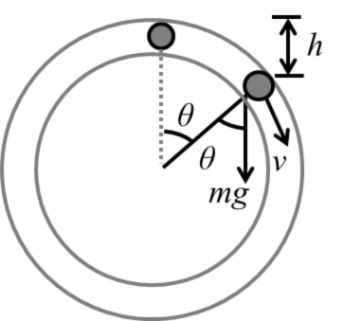
Let N be the normal reaction (away from centre) at angle q.

 

Substituting value of v² from Eq. (i), we get

mg cos q - N = 2 mg (1 – cos q)’

N = mg (3 cos q -2)

(b) The ball will lose contact with the linner space when N = 0

 

After this it makes contact with cover sphere and normal reaction starts acting towards the centre.

 

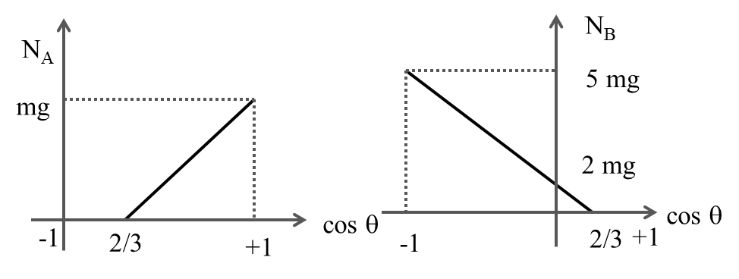
N_B = 0

and     N_A = mg (3 cos q - 2)

 

N_A = 0 and N_B = mg (2 – 3 cosq)

The corresponding graphs are as follows.          

Case III

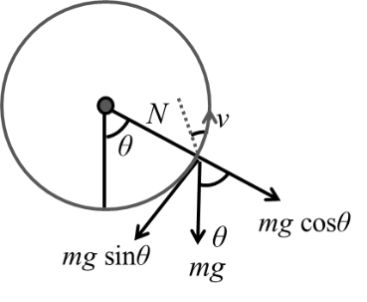
A small smooth block of mass m is projected with speed  from bottom of a fixed sphere of radius, R so that the block moves in a vertical circular path.

Question. The speed of the block as function of q, the angle of deflection from the lowest vertical.

        

Solution: From free body diagram of the block, - mg sin q = ma_t

 

 

 

 

or       v² = 2gR – 2gR (1 – cos q)/

                                                          Answer (b)

Question. Normal reaction at the moment when vertical component of the block’s velocity is maximum.

(a) mg                                             

                                      (d) 2 mg

Solution: From the figure, vertical component of velocity is

 

 

         

 

                              Answer (c)

Question. The angle q between the thread and the lowest vertically at the moment when the total acceleration vector of the block is directed horizontally.

                                                         

                                         

Solution: From the figure, the centripetal acceleration is 

and a tangential acceleration is a_t = a cos q

or    g sin q = a cos q

             a = g tan q

        or      v² = gR tan q sin q

or   2gR cos q = gR tan q sin q

                                Answer (c)