Unit and Dimensions

                          UNITS AND DIMENSIONS

Units “ To measure or represent any physical quantity we need units”

Exception: Although there are few physical quantities which do not

need any unit like refractive index, Relative density or specific gravity etc.

Physical quantity            

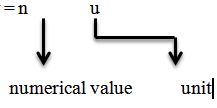
 nu = Constant

 

Example: In a particular system, the unit of length,

mass and time  are chosen to be 10cm, 10gm and 0.1 sec

respectively. The unit of force in this system will be

equivalen to:      

1. 0.1 N
2. 1 N
3. 10 N
4. 100 N

Sol. Unit of force Þ F = ma = Kg metre /sec²

Here   

F = 0.1 N     So the Correct option is (a)

Example: The density of a material in CGS System of unit

is 4gm/cm³. In a system of units in which unit

of length is 10cm and unit of mass is 100 gm the

value of density of material will be     

(a) 0.04

(b) 0.4

(c) 40

(d) 400

Solution. Given n₁ u₁ = 4 gm/cm³

n₂ u₂ = n₁ u₁

 

n₂ = 40                                            Answer (a)

FUNDAMENTAL PHYSICAL QUANTITIES, UNITS, SYMBOLS

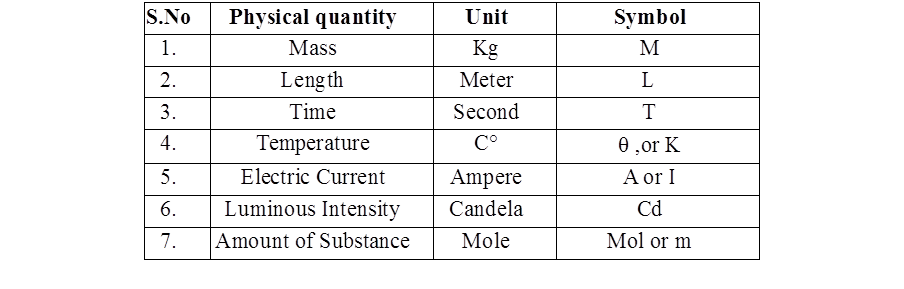
SUPPLEMENTARY UNITS

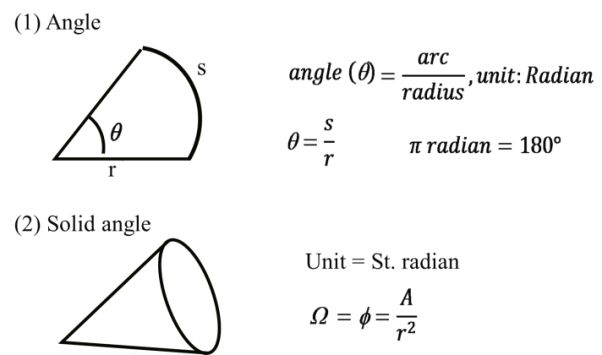
Derived Units: The units which may derive by

fundamental or Supplementry units

Ex. Force= ma = Kg mt/sec²

Conventions adopted while writing a unit

1. Even if a unit is named after a person it should

not be Capital initial letter.

Newton (no)      Joule (no)            Ampere (no)  

     or                      or                            etc.

newton (yes)     joule (yes)          ampere (yes)    

2. In symbol for a unit named after a person

Newton ® N

Ampere ® A

Joule ® J

Watt ® w

3. The symbol or units are not expresse

d in plural form : 50 m (yes) , 10 joule (yes)

                          50 ms (no)  , 10 joules (no)

4. Not more than one Solidus is used

1 poise = 1g/s  cm or 1 gs^-1

Law of homogeneity

Here we can jump through +, - , = (signs)

 

and a,b, c- are Constant then find dimensional formula of a, b, c-

 

Apply Law of homoginity

Dimensional formula of v = dim-formula of at = v

 

Similarly we can say t = c Þ C = [T]

 

b = [L]

Example: The equation of state of some gases can be expressed as here p is pressure, V is the volume, T is temp. then the dimensional formula of Constants a and b will be ?

 

Apply Law of homoginity Dimensional formula of p = Dim-formula of 

a = PV² = ML ^-1T^-2L⁶ =[ML⁵T^-2]

Similarly dimensional formula of v = Dim. Formula of b b = v

= [L³]

ANS a = [ML⁵ T^-2]

b = [L³]

Application No-3

Dimension less quantities or functions

(i) Quantities having units but dimensionless

So all trigonometric functions will be dimension less i.e. sin x, cos  x, tan x – etc.

(ii) Quantities neither having units nor dimension 

Refraction index

Reynolds number, Relative density etc.

(iii) Dimension less mathematical functions

(a) Logarithmic functions: log_e x or log₁₀ x

(b) Exponential functions: e^x, a^x

 

(a) P

(b) R

(c) T

(d) V

 

 

 

 

                    Correct answer is (a)

 

Example Nuclear force between nucleons is given by   Here F is force, r is distance, and c, k are Constants then find dimensional formula of C and k = ?

 

Here e^-kr is dimension less

So C = Fr² = M L T^-2 L² = [M L³ T^-2]

No because e^-kr is dimension less

So k = 1/r

 = [L^-1]

Ans: dimensional formula of

C = [M L³T^-2]

K = [L^-1]

SYSTEMS OF UNITS

(1) MKS AND MKSA SYSTEM

Here in this system M® meter, K® Kilogram, S ®Second and A® ampere

Physical quantity Unit in MKS or MKSA System

 

 

…….. and so on

(2) SI SYSTEM (INTERNATIONAL SYSTEM)

Here in this system unit of physical quantities are use to be named after different great Scientists.

Physical quantity 

Unit in SI System

1. Force ® newton or N
2. Energy ® joule or J
3. Power ® watt or W

(3) CGS SYSTEM

Here  C® Centimeter, G ® gram, S ® Second

Physical quantity  Unit in CGS System

 

 

 

….and so on

(4) FPS SYSTEM

Here  F ® foot, P ® pound , S ® second

Force ® pd ft/ sec², Similarly other physical quantities

Dimensional and dimensional formula

Dimensional formula

Almost all physical quantities can be expressed in terms of the seven fundamental units in symbolic form.

Dimensions 

Dimensions of a physical quantity are the powers to which we must be raised to fundamental quantity represent the given physical quantity.

……. And so on

APPLICATIONS OF DIMENSIONAL FORMULAS

Application No. (1)

To establish results

Suppose any mass m is moving along a circular path of radius R with uniform speed of V. If the force required to do so is F then establish the result or relation between F, m, v and R.

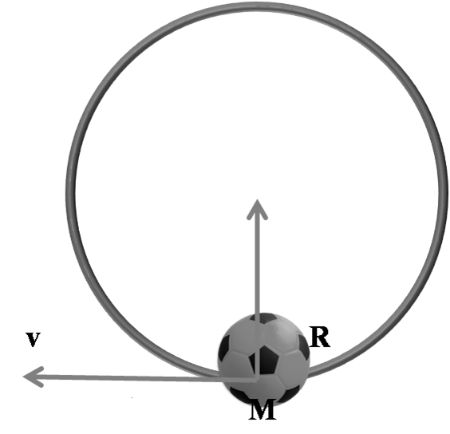
Given ,

F = k  m^x  v^Y R^Z

F a m^x  v^Y R^Z

[M L T ^-2] = K [M] ^x [LT ^-1] ^y [L] ^z

[M LT^-2] = K [M^x L^y+z T^-y ]

Comparing both sides

X =1, y + z = 1, - y = - 2 Þ y = 2

2 + z = 1

Z = 1 - 2 = - 1

By experiment Constant K = 1

So we have result F = m¹ v² R^-1 Þ

Example 1 Given a simple pendulum of very small bob of mass connected with a light String of length l. Also given acceleration due to gravity is g and time period T of simple pendulum depends on mass of the bomb, length of the String l and acceleration due to gravity g then establish   result for T.

Given

T a m ^x l ^y g ^z

T = k m^x l ^y g ^z

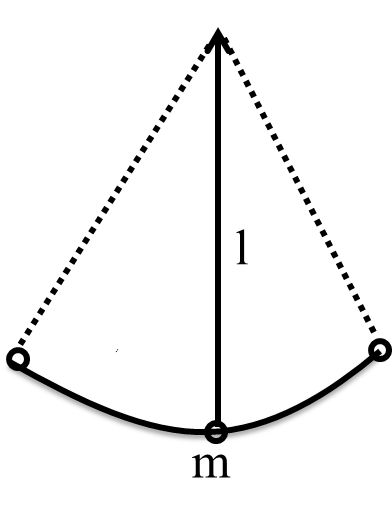
[M° L° T¹] = K [M]^x [L]^y [LT^-2]^z

Þ [M° L° T¹] = k [M ^x L ^{y + z} T ^-2z]

Compare both Side

x = 0, i.e. Time period will not depend on mass of the bob Y + z = 0

Compare both Side

x = 0,i.e. Time period will not depend on mass of the bob Y+ z = 0

 

 

By experiment k = 2p

 

Example: In a system of units , if force F, acceleration A and time T are taken as fundamental units then the dimensional formula of energy is

(a) [F A² T]

(b) [F A T²]

(c) [F² AT]

(d) [FAT]

Solution:  Let energy denote by E

Then E a F^x A^y T^z

E = F^x A^y T^z

[M L² T^-2] = [M L T^-2]^x [ LT^-2]^y [T]^Z

[M L² T^-2] = [M^x L^x+y T^{-2x-2y +z}]

Compare both Sides

x =1 ,         - 2x – 2y + z = -2

x + y = 2    - 2x1 -2 x1 + z = -2

Þ Y = 1    - 4 + z = -2

 Z = 4 – 2  

  Þ Z = 2

Therefore dimensional formula of energy E in Terms of FAT is  [ F¹ A¹ T²] Þ [ FAT²]  Ans B                                 

Application No.2: To check the validity of any result.