Straight line motion, Fixed axis rotation

Kinetic Energy of a Rigid Body Rotating About a Fixed Axis

 

 

  

 

A uniform flat disc of mass M and radius R rotates about a horizontal axis through its center with angular speed  

What is its angular momentum?

                                                    

                                                

 

A chip of mass m breaks of the disc at an instant such that the chip rises vertically above the point at which it breaks off. What is the maximum height the chip rises to from the location of its breaking? (no impulses internal force acts on the chip)

                                                          

                                                            

In the process, the mechanical energy of the chip remains constant.

 

What are the final angular momentum and energy of the disc?

                         

             

 

 

 

EXTRA POINTS TO REMEMBER

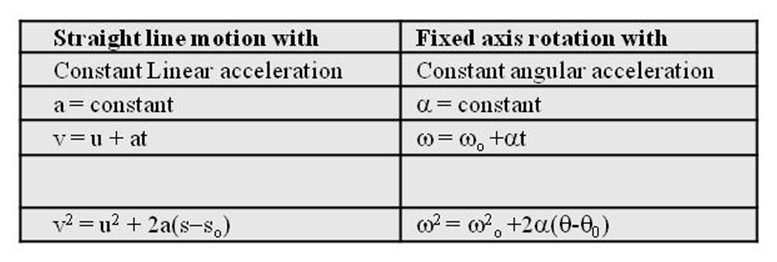
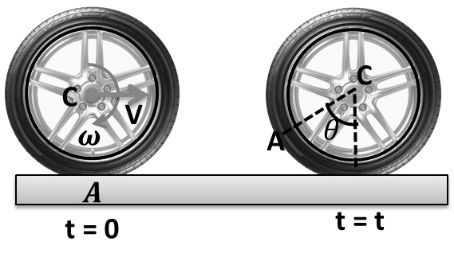
In case of pure rolling on a stationary horizontal ground (when v = Rw), following points are important to note:

Distance moved by the center of mass of the rigid body in one full rotation is 2pR.

This is because  

In forward slipping  s > 2pR

And in backward slipping      s > 2pR 

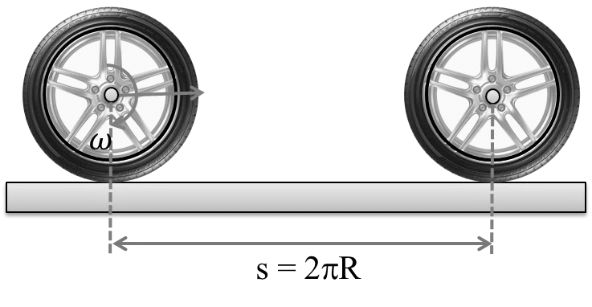
The speed of a point on the circumference of the body at the instant shown in figure is .  

 

This can be shown as:

 

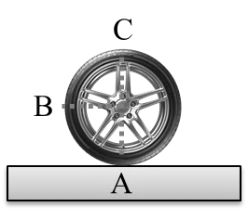
From the above expression we can see that:

 

 

 

The path of a point on circumference is a cycloid and the distance moved by this point in one full rotation is 8R.

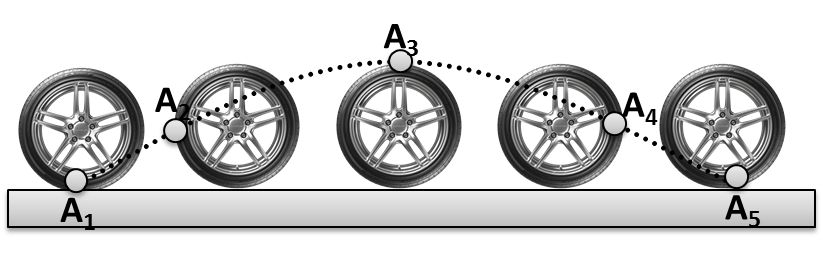
In the figure, the dotted line is a cycloid and the distance A₁A₂…..A5 is 8R. this can be proved    

Speed of point A at this moment is,     

Distance moved by it is in time dt is,           

Therefore, total distance moved in one full rotation is,

 

On integration we get, s = 8R. 

 

 

 

 

Here, K_R stands for rotational kinetic energy  for translation kinetic energy  

For example, for a disc

 

 

 

Case 3

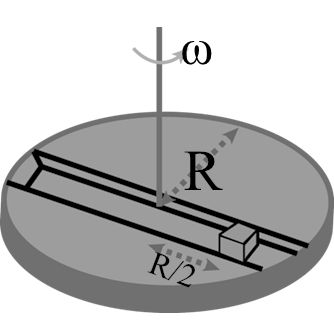
A frame of the reference that is accelerated with respect to an inertial frame of reference is called a non –inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity w is an example of a non –inertial frame of reference. The relationship between the force F_rot experienced by a particle of mass m moving on the rotating disc and the force F_in experienced by a particle of mass m moving on the rotating disc and the force Fin experienced by the particle in an inertial frame of reference is,  , where, vrot is the velocity in the rotating frame of reference and r is the position vector of the particle with respect to the center of the disc.

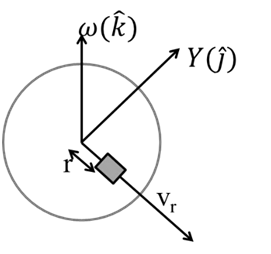
Now, consider a smooth slot along a diameter of a disc of radius R rotating counter –clockwise with  a constant angular speed w about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the X –axis  along the slot, the Y –axis perpendicular to the slot and the z –axis along the rotation axis (w = wk). A small block of mass m is gently placed in the slot at  and is constrained to move only along the slot.

Force on block slot  

 

 

   

 

 

 

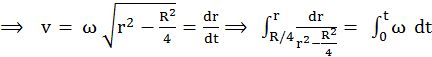
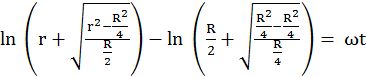
The net reaction of the disc on the block is

                              

 

 

 

 

 

 

 

 

 

 

Also, reaction is due to disc surface then

 

Case 4 

A thin uniform bar lies on a frictionless horizontal surface and is free to move in any way on the surface. Its mass is 0.16 kg and length is m. Two particles, each of mass 0.08 kg are moving on the same surface and towards the bar, one with a velocity 10 ms^-1 and the other with 6 ms^-1 as shown in the figure. The first particle strikers the bar at point A and the other at point B. Each of A and B is at a distance of 0.5 m from the center of the bar. The particle strike the bar at the same instant of time and stick to the bar after collision.

The velocity of center of mass of the system just after impact (in ms^-1) is

(a) 1                            (b) 2                            (c) 3                            (d) 4

Let v be the center of mass is at rest all the times, because of conversation of linear momentum. So, linear velocity of the system must be zero.

From law of conversation of linear momentum.

 

V = 4 ms^-1

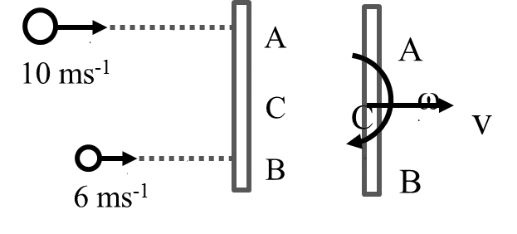
The angular velocity of the system just after impact (in rad/s) is

(a) 8                            (b) 4                            (c) 2                            (d) 1

AC = BC = 0.5 m

From conversation of angular momentum about C

(0.08)(10)(0.5)-(0.08)(6) (0.5)   

Where,     

 

 

Using this in the equation above, we get ω

Case 5

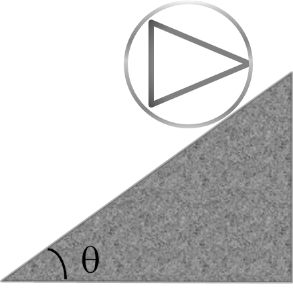
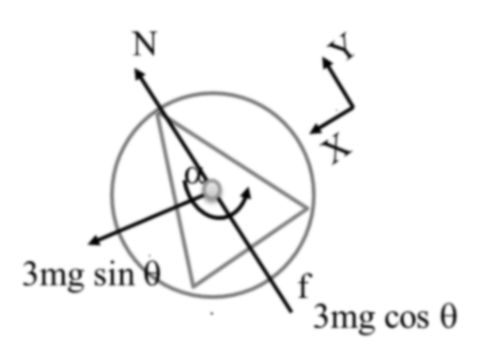
A light ring with three rods, each of mass m is welded on this ring. The rods form an equilateral triangle. The rigid assembly is released on a rough fixed inclined plane. Determine the minimum value of the coefficient of static friction that will allow pure rolling of the assembly.

                                 

                                 

 

                 ….(i)

 

                    ……(ii)

                                                ….(iii)

For no slipping                                   …..(iv)

The moment of inertia of the assembly about its center of mass is

 

Now, on solving Eqs. (i), (ii), (iii) and (iv) simultaneously, we obtain

 

If µ is the coefficient of fricti on at the contact surface, then