Product of Vectors

  

   

 

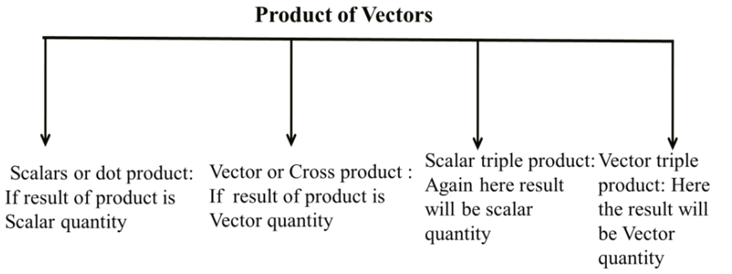
Note: Vector triple product is not in our Physics syllabus.                                                                                                                                                                                                                   

SCALAR OR DOT PRODUCT

   Product of magnitude of two Vectors with cosine of angle between them.

     

    

    

   For perpendicular Vectors: ,q = 90° and cos 90° = 0

              

    

             

     

 Dot product of Standard unit Vectors:

                                                                                                     

                                                                                                        

        

  are mutually perpendicular then

the value of m is

      (a) - 2

      (b) - 3

      (c) + 3

      (d) + 2

            

          

  2 + m + 1 = 0

  m = - 3                                                                                           Answer (b)  

  Method to find dot or Scalar product

   

   

   

  Finding Scalar and Vector Component (projection)

     

       

          

    

  

  

         

  

       

   

   

   

  

   

   

   

   

                     

                      

   

  

  Component (projection) in the direction and in the perpendicular direction

   

   

   

   

   

   

   

   

              

           vector or cross product   

    Product of magnitude of two Vectors with sine of angle between them.

    

    

   For perpendicular Vectors:

    

   For parallel Vectors:

    

    

    

   For antiparallel Vectors:

    

    

    

   Cross or Vector product of Standard unit vectors

    

    

   USING RIGHT HAND SCREW RULE

   

   Method to find cross or vector product

    

    

    

    

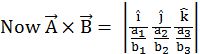
          AREA OF TRIANGLE 

    

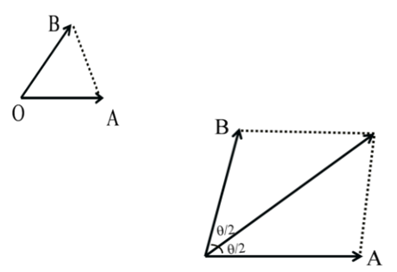
   Area of parallelogram:

    

         DIAGONAL OF PARALLELOGRAM

   Example If the diagonals of a parallelogram are and  ,then area of this

   parallogram will be

     (a) 2 unit²                                        (b) 3 unit²

     (c) 4 unit²                                        (d) 1 unit²

    

    

    

    

    

   = 2 unit²                                                         Answer (a)

   Example: Unit vector perpendicular to two vectors Finding a unit vector

   perpendicular to

    

    

    

    

    

     

    

    

    

   Example: Consider three Vectors

   Scalar triple product

    

    

    

    

   

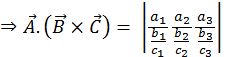
    (a) 0

    (b) 6

    (c) 12

    (d) 18

    

    

   = 2 (3 n-2) -3 (15 + 1) -2 (10 + n) = 0

   4n – 72 = 0

   n = 18                                                         Answer (d)