MOMENT OF INERTIA OF A SINGLE PARTICLE

I = mr2
![]()
MOMENT OF INERTIA OF A RIGID BODY

![]()
Theorem on Moment of Inertia
Theorem of Parallel Axis
I = Icm +Mr2

Theorem of Perpendicular Axis
Moment of Inertia is independent of Mass depend on distribution of mass
![]()
![]()

Moment of inertia of some regular shaped rigid bodies
![]()

![]()

![]()
![]()

![]()

![]()

![]()

RADIUS OF GYRATION
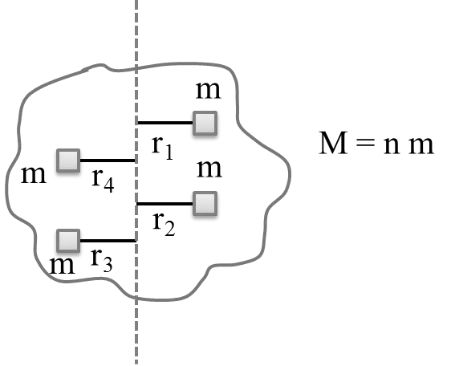
Let mass of the rigid body = M
Now I = S mr2
![]()
![]()
![]()
![]()
Here K is radius of gyration
RMS value of ![]()
Case I
A thin disc of mass M and radius R has mass per unit area![]() where r is the distance from its center. Its moment of inertia about an axis going through its center of mass and perpendicular to its plane is
where r is the distance from its center. Its moment of inertia about an axis going through its center of mass and perpendicular to its plane is
Given, surface mass density, ![]()
So, mass of the disc can be calculated by considering small element
of area 2prdr on it and then integration it for complete disc, i.e.
![]()
![]()
![]()
![]() ….(i)
….(i)
Moment of inertia about the axis of the disc,
![]()
![]()
![]()
Case II
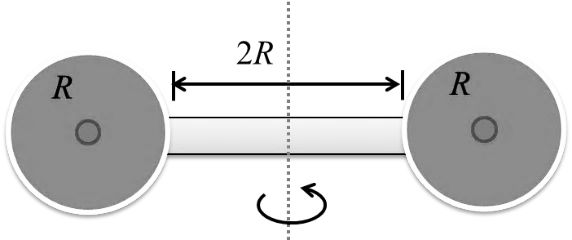
Two identical spherical balls of mass M and radius R each are suck on two ends of a rod of length 2R and mass M (see figure). The moment of inertia of the system about the axis passing perpendicularly through the center of the rod is Key idea This problem will be solved by applying parallel axis theorem, which states that moment of inertia of a rigid body about any axis is equals to its moment of inertia about a parallel axis through its center of mass plus the product of the mass of the body the square of the perpendicular distance between the axis.
We know that moment of inertia (MI) about the principle axis of the sphere is given by
![]()
Using parallel axis theorem, moment of inertia about the given axis
![]()
![]()
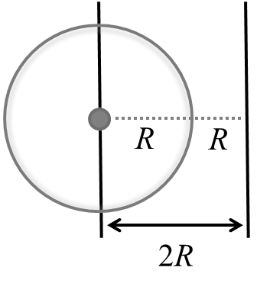
Considering both sphere at equal distance form the axis, moment of inertia due to both sphere about this axis will be
![]()
Now, moment of inertia of rod about its perpendicular bisector axis is given by
![]()
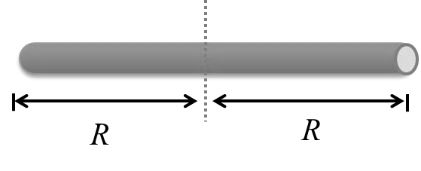
Here, given that
L = 2R
![]()
So, total moment of inertia of the system is
![]()
![]()
Case III
Seven identical circular planner discs, each of mass M and radius R are welded symmetrically The moment of inertia of the arrangement about an axis normal to the plane and passing through the point P is
From theorem of parallel axis,
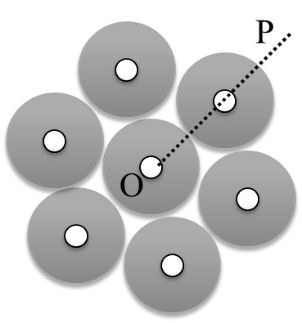
![]()
![]()
Case IV Cavity
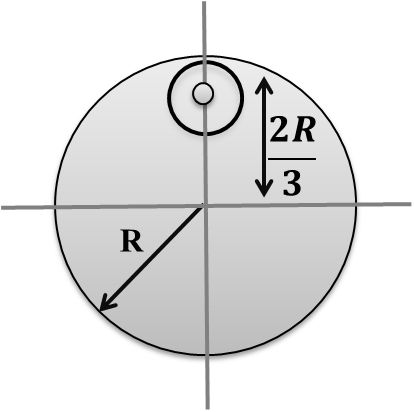
Form a uniform circular disc of radius R and 9M, a small disc of radius ![]() is removed The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through center of disc is
is removed The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through center of disc is
![]()
Case V
The moment of inertia of a uniform cylinder of length l and radius R about its perpendicular bisector is I. what is the ratio l/R such that the moment of inertia is minimum?

MI of a solid cylinder about its perpendicular bisector of length is
![]()
![]()
![]()
For I to be minimum,
![]()
![]()
![]()
![]()
![]()
![]()
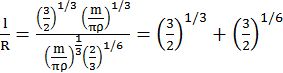
![]()
Case:- Moment of Inertia
Rod → mass = m, Length = L
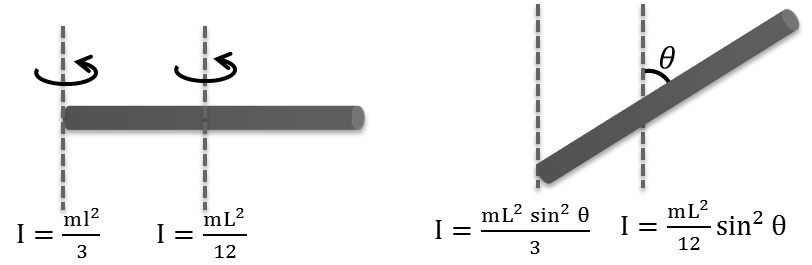
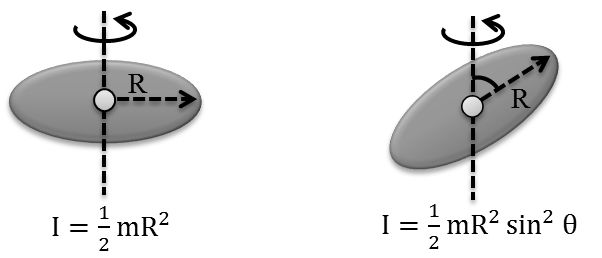
Disc → mass = m, Radius = R
Multiple rods
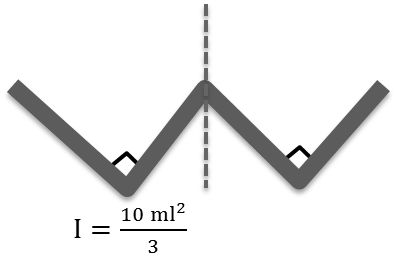
Each rod of mass m and length L
![]()
![]()
![]()
![]()
![]()
Torque of Force about the Axis of Rotation
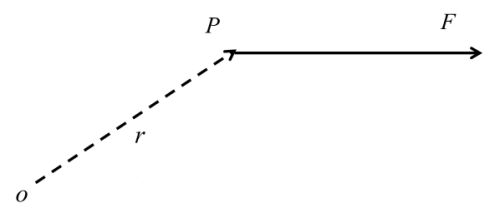
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Case 1
A cylinder uniform rod of mass M and length l is pivoted at one end so that it can rotate in a vertical plane (see the figure). There is negligible friction at the pivot. The free end is held vertically above the pivot and then released. The angular acceleration of the rod when it makes an angle q with the vertical, is
As the rod rotates in vertical plane so a torque is acting on it, which is due to the vertical component of weight of rod.
Now, Torque t = force x perpendicular distance of line of action of force from axis of rotation
![]()
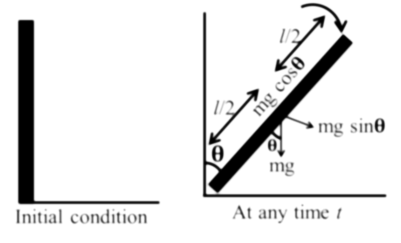
Again, Torque, t = Ia
Where, I = moment of inertia =![]()
[forced and Torque frequency along axis of rotation
passing through in end]
a = angular acceleration
![]()
![]()
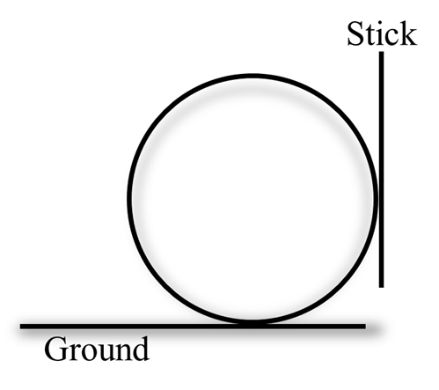
A boy is pushing a ring of mass 2 kg and radius 0.5 m with a stick as shown in the figure. The stick as shown in the figure of 2N on the ring rolls it without slipping with an acceleration of 0.3 m/s2. The coefficient of friction between the ground and the ring is large enough that rolling always occurs and the coefficient of friction between the stick and the rings is ![]() .
.
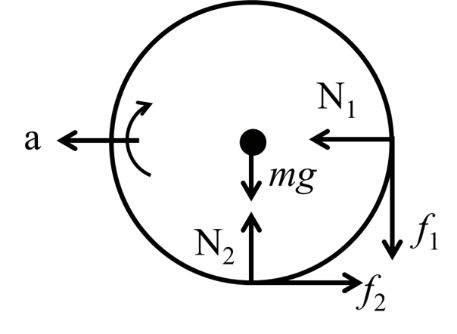
There is no slipping between ring and ground. Hence f2 is not maximum. But there is slipping between ring and stick. Therefore f1 is maximum. Now let us write the equations
![]()
![]()
![]()
![]()
![]()
![]()
Solving above four equations we get,![]()

 Kaysons Publication
Kaysons Publication
