Fundamental Physical Quantities, Unit, Symbols
UNITS AND DIMENSIONS
Units “ To measure or represent any physical quantity we need units”
Exception: Although there are few physical quantities which do not
need any unit like refractive index, Relative density or specific gravity etc.
Physical quantity
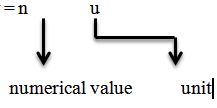
nu = Constant
![]()
Example: In a particular system, the unit of length,
mass and time are chosen to be 10cm, 10gm and 0.1 sec
respectively. The unit of force in this system will be
equivalen to:
- 0.1 N
- 1 N
- 10 N
- 100 N
Sol. Unit of force Þ F = ma = Kg metre /sec2
Here ![]()
F = 0.1 N So the Correct option is (a)
Example: The density of a material in CGS System of unit
is 4gm/cm3. In a system of units in which unit
of length is 10cm and unit of mass is 100 gm the
value of density of material will be
(a) 0.04
(b) 0.4
(c) 40
(d) 400
Solution. Given n1 u1 = 4 gm/cm3
n2 u2 = n1 u1
![]()
n2 = 40 Answer (a)
FUNDAMENTAL PHYSICAL QUANTITIES, UNITS, SYMBOLS
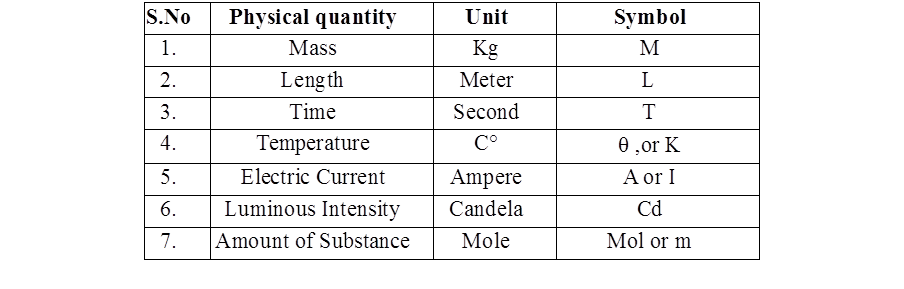
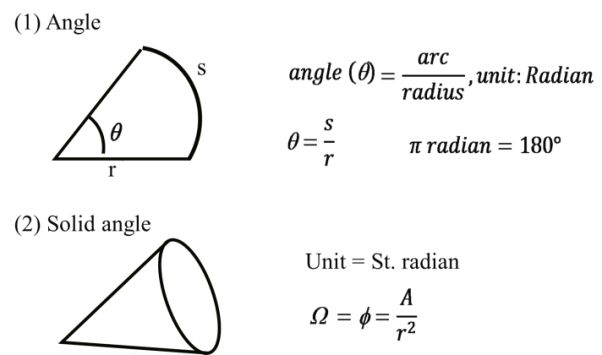
SUPPLEMENTARY UNITS
Derived Units: The units which may derive by
fundamental or Supplementry units
Ex. Force= ma = Kg mt/sec2
Conventions adopted while writing a unit
1. Even if a unit is named after a person it should
not be Capital initial letter.
Newton (no) Joule (no) Ampere (no)
or or etc.
newton (yes) joule (yes) ampere (yes)
2. In symbol for a unit named after a person
Newton ® N
Ampere ® A
Joule ® J
Watt ® w
3. The symbol or units are not expresse
d in plural form : 50 m (yes) , 10 joule (yes)
50 ms (no) , 10 joules (no)
4. Not more than one Solidus is used
1 poise = 1g/s cm or 1 gs-1
Errors
ERRORS
The result of every measurement by any measuring instrument contains some uncertainty this uncertainty is called errors. The errors in a measurement is equal to the difference between the true value and the measured value of any quantity.
Errors = True value – Measured value
Absolute Errors:- the several values obtained in an experiment measured are a1, a2, a3….an the arthmetic mean of these values will be
![]()
Now error in first measurement = Da1 = amean –a1
Similarly in second measurement = Da2 = amean –a2 and so on
![]() Relative error:Relative error=∆ameanamean
Relative error:Relative error=∆ameanamean![]()
![]()
Combination of errors (maximum possible error) Addition or subtraction
![]()
![]()
Product or multiplication
Let
![]()
![]()
Division
![]()
![]()
![]()
(4) Powers
Let C = anbm
![]()
CONCEPT WITH EXAMPLES
Role of constants
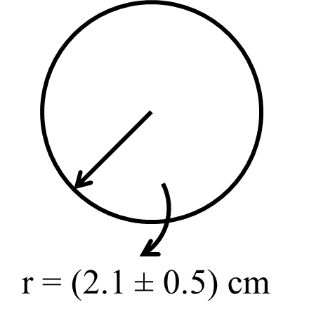
The radius of sphere is measured to be (2.1 ± 0.5) cm and is surface area with error limits.
Solution:
Surface area = A = 4pr2
![]()
![]()
![]()
Now% error
![]()
= 47.62 %
Other way
= 4 p r2
![]()
= 55.4 cm2
![]()
![]()
![]()
= 26.4 cm2
Now (A ± DA)
= (55.4±26.4)![]()
FINDING QUANTITY
Percentage error in determining of acceleration of gravity with the help of simple Pendulum time period .![]() Given error in length of pendulum 4% while in The time period it is 2% then percentage error in g = ?
Given error in length of pendulum 4% while in The time period it is 2% then percentage error in g = ?
Solution
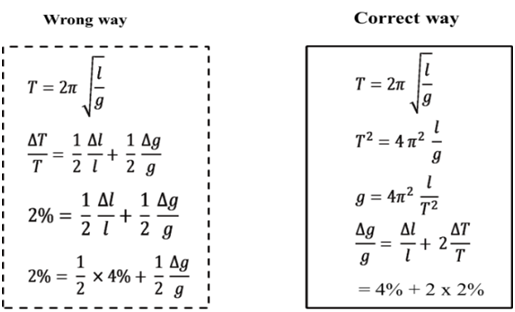
![]()
LEAST COUNT AND DIFFERENT UNITS
If a particle of mass m = 25.0 Kg is moving in a circular path of radius r = 50.00 cm with constant speed of v = 10.0 Km/hr them find error in force required by particle.
Now Given
m = 25.0 Kg
= L.c. = 0.1
V = 10.0 Km/h
= L.c = 0.1
DV = 0.1, V = 10
R = 50.00 cm
Dr = 0.001, r = 50cm
NOTE: never change units in error.
Least count
25.00 – L.c = 0.01
16.50 – 50 –L.c = 0.01
76.03 – 03 –L.c = 0.01
15.0002 –L.c = 0.0001
17.030 – L.c = 0.01
Solution:
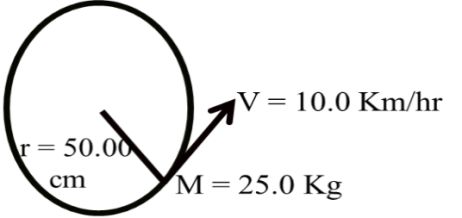
![]()
![]()
![]()
![]()
![]()
![]()
= 1.21 x 2= 2.42% Ans.
UNIQUE CONCEPT
Calculate focal length of a spherical Mirror from the following observations Object distance u = (50.1 ± 0.5) cm. and image distance v = (20.1 ± 0.2) cm.
![]()
![]()
![]()
= 14.3 cm
Now
![]()
![]()
![]()
![]()
![]()
± 0.4 cm
Note: Similar case in resistance connected in parallel combinations
![]()
SIGNIFICANT FIGURES
The number of significant figures of a numerical quantity is the number of reliably known digits it contains:
Rules:
1. Zeros at the beginning of a number are not significant.
Ex. 0.0523 – there S.f. (5, 2, 3)
2. Zeros within a number are significant.
Ex: 2056 –Four S.f. (2, 0, 5, 6)
3. Zeros at the end of a number after decimal points are significant.
Ex. 3702.0 –five S.f. (3, 7, 0, 2, 0)
Homogeneity
Law of homogeneity
Here we can jump through +, - , = (signs)
![]()
and a,b, c- are Constant then find dimensional formula of a, b, c-
![]()
Apply Law of homoginity
Dimensional formula of v = dim-formula of at = v
![]()
Similarly we can say t = c Þ C = [T]
![]()
b = [L]
Example: The equation of state of some gases can be expressed as ![]() here p is pressure, V is the volume, T is temp. then the dimensional formula of Constants a and b will be ?
here p is pressure, V is the volume, T is temp. then the dimensional formula of Constants a and b will be ?
![]()
Apply Law of homoginity Dimensional formula of p = Dim-formula of ![]()
a = PV2 = ML -1T-2L6 =[ML5T-2]
Similarly dimensional formula of v = Dim. Formula of b b = v
= [L3]
ANS a = [ML5 T-2]
b = [L3]
Application No-3
Dimension less quantities or functions
(i) Quantities having units but dimensionless

So all trigonometric functions will be dimension less i.e. sin x, cos x, tan x – etc.
(ii) Quantities neither having units nor dimension
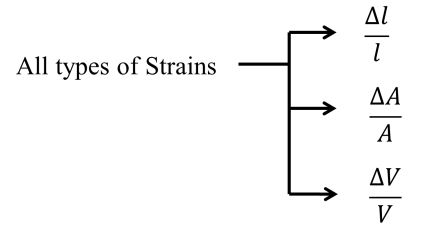
Refraction index![]()
Reynolds number, Relative density etc.
(iii) Dimension less mathematical functions
(a) Logarithmic functions: loge x or log10 x
(b) Exponential functions: ex, ax
![]()
(a) P
(b) R
(c) T
(d) V
![]()
![]()
![]()
![]()
![]() Correct answer is (a)
Correct answer is (a)
Example Nuclear force between nucleons is given by![]() Here F is force, r is distance, and c, k are Constants then find dimensional formula of C and k = ?
Here F is force, r is distance, and c, k are Constants then find dimensional formula of C and k = ?
![]()
Here e-kr is dimension less
So C = Fr2 = M L T-2 L2 = [M L3 T-2]
No because e-kr is dimension less
So k = 1/r
= [L-1]
Ans: dimensional formula of
C = [M L3T-2]
K = [L-1]
Systems of Units, Dimensional Formluas
SYSTEMS OF UNITS
(1) MKS AND MKSA SYSTEM
Here in this system M® meter, K® Kilogram, S ®Second and A® ampere
Physical quantity Unit in MKS or MKSA System
![]()
![]()
![]()
…….. and so on
(2) SI SYSTEM (INTERNATIONAL SYSTEM)
Here in this system unit of physical quantities are use to be named after different great Scientists.
Physical quantity
Unit in SI System
- Force ® newton or N
- Energy ® joule or J
- Power ® watt or W
(3) CGS SYSTEM
Here C® Centimeter, G ® gram, S ® Second
Physical quantity Unit in CGS System
![]()
![]()
![]()
….and so on
(4) FPS SYSTEM
Here F ® foot, P ® pound , S ® second
Force ® pd ft/ sec2, Similarly other physical quantities
Dimensional and dimensional formula
Dimensional formula
Almost all physical quantities can be expressed in terms of the seven fundamental units in symbolic form.
Dimensions
Dimensions of a physical quantity are the powers to which we must be raised to fundamental quantity represent the given physical quantity.
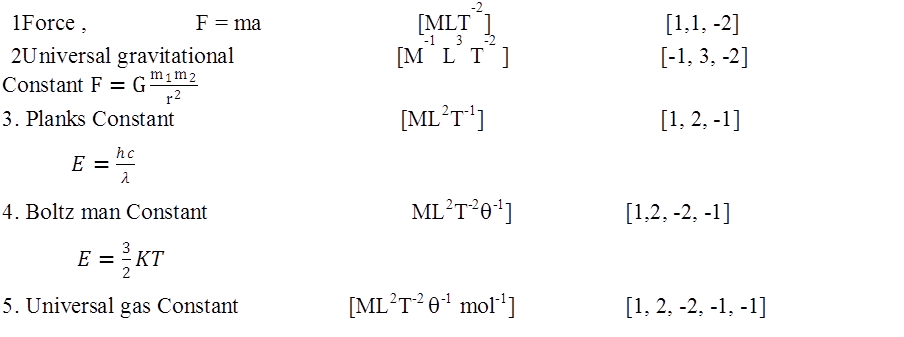
……. And so on
APPLICATIONS OF DIMENSIONAL FORMULAS
Application No. (1)
To establish results
Suppose any mass m is moving along a circular path of radius R with uniform speed of V. If the force required to do so is F then establish the result or relation between F, m, v and R.
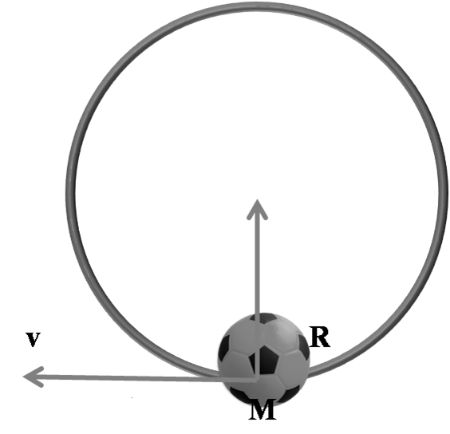
Given ,
F = k mx vY RZ
F a mx vY RZ
[M L T -2] = K [M] x [LT -1] y [L] z
[M LT-2] = K [Mx Ly+z T-y ]
Comparing both sides
X =1, y + z = 1, - y = - 2 Þ y = 2
2 + z = 1
Z = 1 - 2 = - 1
By experiment Constant K = 1
So we have result F = m1 v2 R-1 Þ![]()
Example 1 Given a simple pendulum of very small bob of mass connected with a light String of length l. Also given acceleration due to gravity is g and time period T of simple pendulum depends on mass of the bomb, length of the String l and acceleration due to gravity g then establish result for T.
Given
T a m x l y g z
T = k mx l y g z
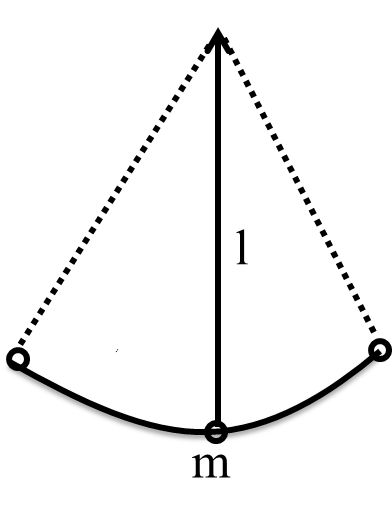
[M° L° T1] = K [M]x [L]y [LT-2]z
Þ [M° L° T1] = k [M x L y + z T -2z]
Compare both Side
x = 0, i.e. Time period will not depend on mass of the bob Y + z = 0
Compare both Side
x = 0,i.e. Time period will not depend on mass of the bob Y+ z = 0
![]()
![]()
By experiment k = 2p
![]()
Example: In a system of units , if force F, acceleration A and time T are taken as fundamental units then the dimensional formula of energy is
(a) [F A2 T]
(b) [F A T2]
(c) [F2 AT]
(d) [FAT]
Solution: Let energy denote by E
Then E a Fx Ay Tz
E = Fx Ay Tz
[M L2 T-2] = [M L T-2]x [ LT-2]y [T]Z
[M L2 T-2] = [Mx Lx+y T-2x-2y +z]
Compare both Sides
x =1 , - 2x – 2y + z = -2
x + y = 2 - 2x1 -2 x1 + z = -2
Þ Y = 1 - 4 + z = -2
Z = 4 – 2
Þ Z = 2
Therefore dimensional formula of energy E in Terms of FAT is [ F1 A1 T2] Þ [ FAT2] Ans B
Application No.2: To check the validity of any result.
Errors,Vernier calipers and Screw Gauge
VERNIER CALIPERS
To measure length accurately upto 0.1 mm or 0.01 mm Vernier Calipers and Screw gauge are used

VERNIER CALIPERS
Parts of Vernier Calipers
(i) Main scale
(ii) Vernier Scale
(iii) Metallic Strip
PRINCIPLE OF VERNIER CALIPERS
N VSD = (n -1) MSD
![]()
1 MSD -1VSD = 1 MSD ![]()
![]()
LC or VC ® Smallest distance that can be accurately measured with
Vernier Scale
![]()
READING A VERNIER CALIPERS
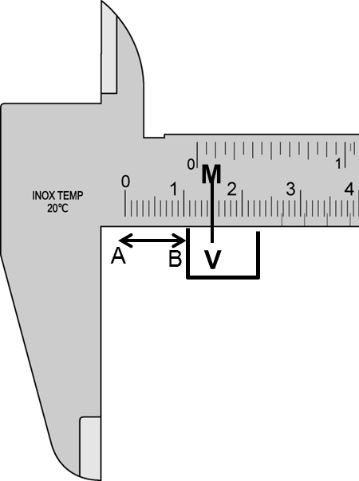
If we have to measure a length AB, the end A is coincided with the zero of main scale, suppose the end B lies between 1.0 cm and 1.1 cm on the main scale. Then,
![]()
Let 5th division of Vernier scale coincides with 1.5 cm of main scale.
Then, ![]()
Thus, we can make the following formula,
Total reading = N + n x VC
Here, N = main scale reading before on the zero of the Vernier scale.
n = number of Vernier division which just coincides with any of the
main scale division.
Zero Error and Zero Correction
If the zero of the Vernier scale does not coincide with the zero
of main scale when jaw B touches A and the straight edge of D
touches the straight edge of C, then the instrument has an error called zero error. Zero error is always algebraically subtracted from measured length.
Zero correction has a magnitude equal error but its given is opposite to that of the zero error. Zero correction is always algebraically added to measured length.
Zero error ® algebraically subtracted
Zero correction ® algebraically added
POSITIVE AND NEGATIVE ZERO ERROR

If zero of Vernier scale lies right of the main scale the zero is positive and if it lies to the left of the main scale the zero error is negative (when jaws A and B are in contact)
Positive zero error = (N + x x VC)
Here, N = main scale reading on the left of zero of Vernier scale.
X = Vernier scale division which coincides with any main scale division.
When the Vernier zero lies before the main scale zero the error is said to be negative zero error. If 8th Vernier scale division coincides with the main scale division, then
Negative zero error = -[0.00 cm + 8 x VC]
= -[0.00 cm +8 x 0.01 cm]
= -0.08 cm
SUMMARY
1. VC=LC=1MSDn=Smallest division on main scale number of division on vernier scale=1 MSD-1VSD![]()
2. In ordinary Vernier calipers, 1 MSD = 1mm and n = 10
![]()
3. Total reading = (N + n x VC)
4. Zero correction = -zero error
5. Zero error is algebraically subtracted white the zero correction is algebraically added.
6. If zero of Vernier scale lies to the right of zero of main scale the error is positive. The actual length in this case is less than observed length.
7. if zero of Vernier scale lies to the left of zero of main scale the error is negative and the actual length is more than the observed length.
8. Positive zero error = (N + x x VC)
Example
The smallest division on main scale of a Vernier calipers is 1 mm and 10 Vernier division coincide with 9 main scale divisions. While measuring the length of a line, the zero mark of the Vernier scale lies between 10.2 cm and 10.3 cm and the third division of Vernier scale coincides with a main scale division.
(a) Determine the least count of the calipers
(b) Find the length of the line
Solution: ![]()
![]()
![]()
SCREW GAUGE
Principle of a Micrometer Screw
The least count of Vernier calipers ordinarily available in the laboratory is 0.01 cm. when lengths are to be measured with greater accuracy, say upto 0.001cm, screw gauge and speedometer are used which are based on the principle of micrometer screw
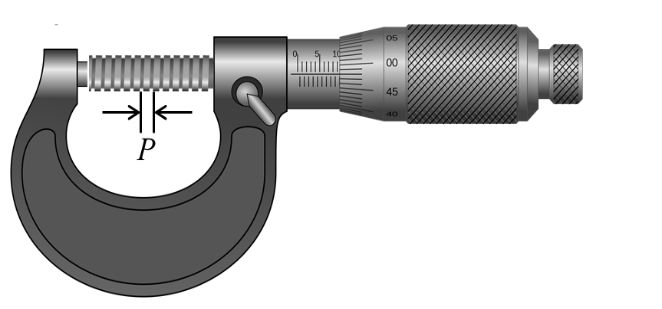
If an accurately cut single threaded screw is rotated in a closely fitted nut, then in addition to the circular motion of the screw there is a linear motion of the screw head in the forward or backward direction, along the axis of the screw. The linear distance moved by the screw, when it is given one complete rotation is called the pitch (p) of the screw. This is equal to the distance between two consecutive threads as measured along the axis of the screw. In most of the cases, it is given one complete rotation is called the pitch (p) of the screw. In most of the cases, it is either 1 mm or 0.5 mm. A circular cap is fixed on one end of the screw and the circumference of the cap is normally divided into 100 or 50 equal parts. If it is divided into 100 equal parts,
then the screw moves forward or backward by ![]() of the pitch, if the circular scale is rotated through one circular scale division. It is circular scale division. It is the minimum distance which can be accurately measured and so called the least Count (LC) of the screw.
of the pitch, if the circular scale is rotated through one circular scale division. It is circular scale division. It is the minimum distance which can be accurately measured and so called the least Count (LC) of the screw.
Thus, ![]()
If pitch is 1 mm and there are 100 divisions on circular scale then,
![]()
= 0.001cm = 10mm
Since, LC is of the order of 10mm, the screw is called micrometer screw.
SCREW GAUGE
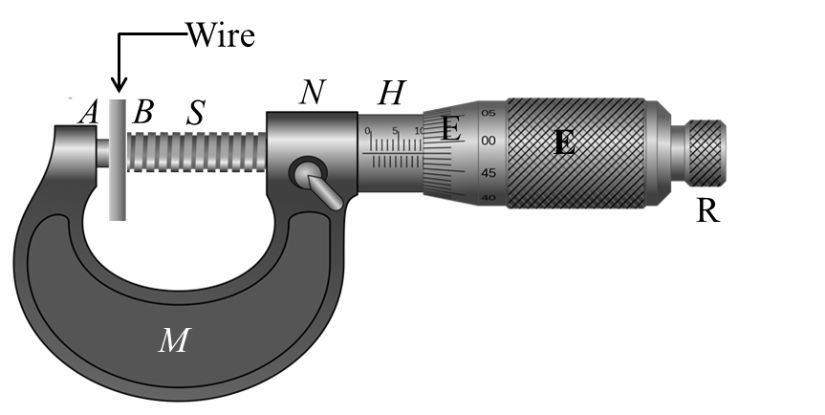
SCREW GAUGE
Screw gauge works on the principle of micrometer screw. It consists of a U –Shaped metal frame M. At one end of its is fixed a small metal piece A. it is called stud and it has a plane face. The other end N of M carries a cylindrical millimeter depending upon the pitch of the screw. This scale is called linear scale or pitch scale.
A nut is threaded through the hub and the frame N. through the nut moves a screw S. the fount face B of the screw, facing the plane face A is also plane, A hollow cylindrical cap K is capable of rotating over the hub when screw is rotated. As the cap is rotated the screw either moves in head scale. In an accurately adjusted instrument when the face A and B are just touching each other. Zero of circular scale should coincide with zero of linear scale.
To measure Diameter of a given wire using a screw gauge
If with the wire between plane faces A and B, the edge of the cap lies ahead of N th division of linear scale, and nth division of circular scale lies over reference line.
Then, Total reading = N + n x LC
ZERO ERROR AND ZERO CORRECTION
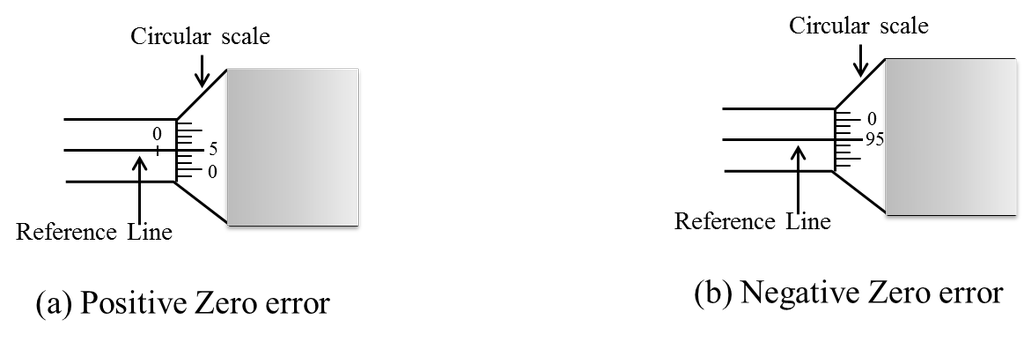
ZERO ERROR AND ZERO CORRECTION
If zero mark of circular scale does not coincide with the zero of the pitch scale when the faces A and B are just touching each other, the instrument is acid to possess zero error. If the zero of the circular scale advance beyond the reference line the zero is positive and zero correction is positive. If it is left behind the reference line the zero is positive and zero negative. For example, if zero of circular scale advance beyond the reference line by 5 divisions, zero correction = + 5 x (LC) and if the zero of circular scale is left behind the reference line by 6 divisions, zero corrections = -5 x (LC)
Example The pitch of a screw gauge is 1 mm and there are 100 divisions on circular scale. When faces A and B are just touching each without putting anything between the studs 32nd divisions of the circular scale (below its zero) coincides with the reference line. When a glass plate is placed between the studs, the linear scale 4 division and the circular scale reads 16 divisions. Find the thickness of the glass plate. Zero of linear scale is not hidden from circular scale when A and B touches each other.
Solution: ![]()
= 0.01 mm
As zero is not hidden from circular scale when A and B touches each other. Hence, the screw gauge has positive error.
![]()
Linear scale reading = 4 x (1mm) =4 mm
Circular scale reading = 16 x (0.01 mm) = 0.16mm
Measured reading = (4 + 0.16)mm = 4.16mm
Absolute reading = Measured reading = -e = (4.16 – 0.32) mm = 3.84 mm
Therefore, thickness of the glass plate is 3.84 mm.
Physical quantity,product of vector and lami's theorem
VECTOR AND SCALARS
Physical Quantity
May have numerical value, units and any specified direction.
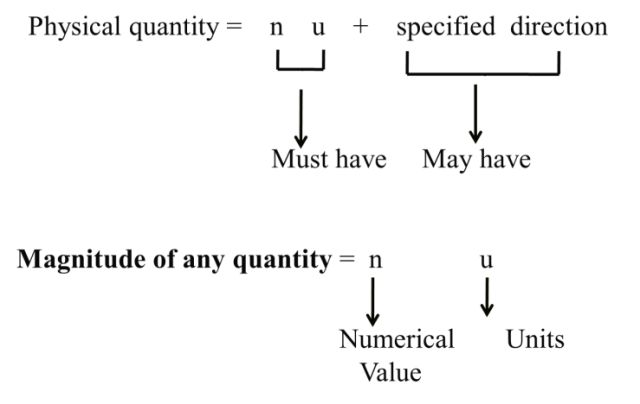
Note:- Some physical quantities only having numerical value not specified direction.
Ex:- Refractive index, strain etc.
We can say any physical quantity Must/may have numerical value(n), unit (u) and specified direction.
PHYSICAL QUANTITY (N + U + DIRECTION) MAY/MUST HAVE

Note:
Scalars or zero order tensors: Any physical quantity have only one component.
Vectors or first order tensors: Any physical Quantity have component greater then one but less than or equal to four.
REPRESENTATION OF VECTOR:

Types of vectors
(1) Polar Vectors:
Vectors related to linear motion of any object Ex. Displacement, velocity, Force etc.
(2) Axial vectors:
Vector represent rotational effect and are always along the axis of rotation Ex: Angular velocity, torque, angular momentum etc.
(3) Null vector or zero vectors:
Vector whose magnitude is zero and direction in determinant.
(4) Unit vectors:
Vector having magnitude equals to one (unity) but must be some specified direction representation of unit vector – , A![]()
![]()
STANDARD UNIT VECTOR
These are ![]()
Direction should be on your copy
UNDERSTANDING OF UNIT VECTORS
1 –D Motion: Motion along x or y or z
A car is moving with 60 k/m toward or due east then speed (scalar) = 60 km/h
Velocity (Vector) = 60 km/h
2 –D Motion:
A car is moving with 60 k/m due north – east then
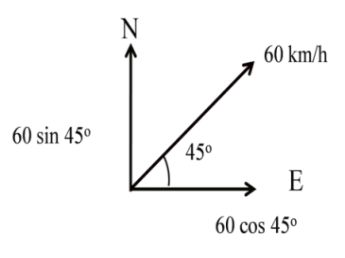
![]()
![]()
2 –D vector
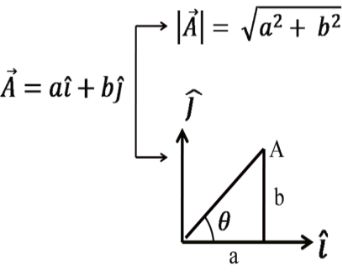
![]()
With x axis or with horizontal
![]()
With Y-axis or with vertical
3 –D Vector
![]()
![]()
![]()
![]()
DIRECTION
![]()
With x-axis
![]()
With y-axis
![]()
With z-axis
ADDITION AND SUBSTRACTION OF VECTORS
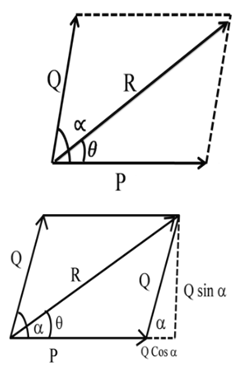
Law of parallelogram
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
RESOLVING OF ANY VECTOR
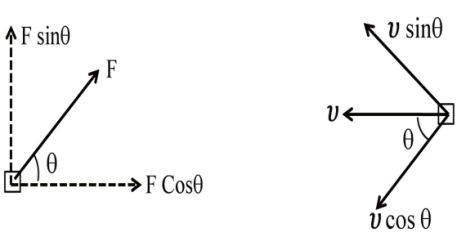
Example. Two equal vector have a resultant equal to either of the two. The angle between them is
(a) 90o (b) 60o
(c) 120o (d) 0o
Solution: By using expression R2 = P2 + Q2 + 2PQ cosa
![]()
x2 = 2x2 (1 + cosa)
![]()
cos a = -1/2 = a = 120o Answer is (c)
Example: Two vector having equal magnitude of x units acting at an angle of 450 have resultant ![]() units the value of x is
units the value of x is
(a) 0 (b) 1
(c) ![]() (d)
(d) ![]()
Solution: Using the expression R2 = P2 + Q2 + 2PQ cosµ
![]()
![]()
![]()
![]()
![]()
Þ x2 =1 Ans (b) Þ x = 1 Ans (b)
![]()
(a) 0° (b) 180°
(c) 90° (d) 120°
![]()
![]()
= 4PQ cos q = 0
Cos q = 0
q = 90o Answer is (c)
LAMI’S THEOREM
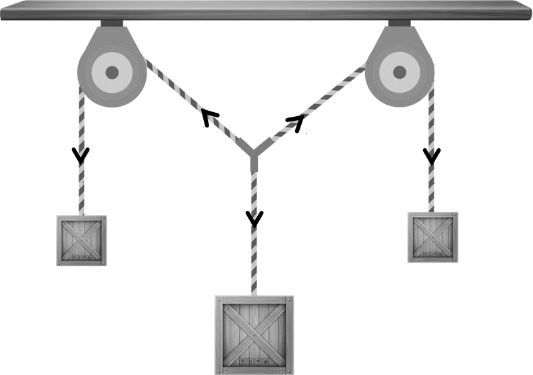
![]()
Kinematics

KINEMATICS
Rest and motion:-
Rest: “if position of any object or particle is not changing with respect to any observer then this object is said to be at rest”
Motion: “if position of any object or particle is changing with respect to any observers then this object is said to be in motion”
“Absolute rest and absolute motion is impossible”
Sate of rest and motion depends upon reference frame (State of observer)
Type of motion
(1) One dimensional (1-D) motion:
If position of any object is changing any of x axis, or y-axis or z axis.
All 1-D motion will be always straight line motion”
(2) Two dimensional (2-D) motion (Motion in a plane)
X-Y plane
Z- X plane
Y-Z plane
“ If position of Any object is changing in x –y or y-z or z-x plane”
Example:
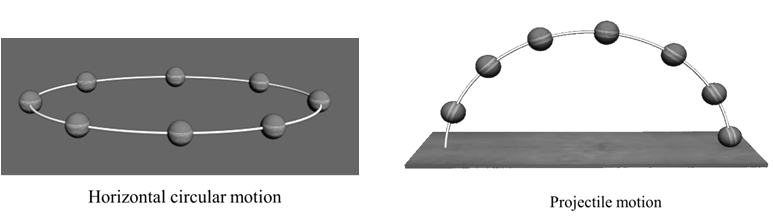
2-D motion may be straight line motion”
“Writing on board or copy is also 2-D event”
(3) Three dimensional (3-D) motion:-
“ if position of any object is changing along all 3 – axis (x-y z)”
Example:-

Human can move in 1-D, 2-D, or 3-D motion”

![]()
BASIC TERMS IN KINEMATICS
(1) Displacement:
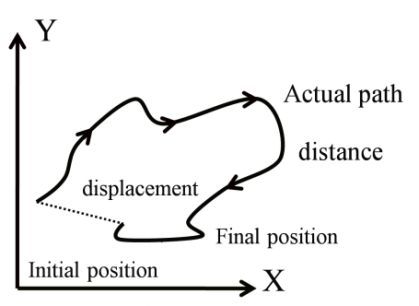
“length of straight line drawn between initial and final position
of any object”
“Shortest path between initial and final position of any object”
It is vector quantity so it may be +, - , zero.
(2) Distance:-
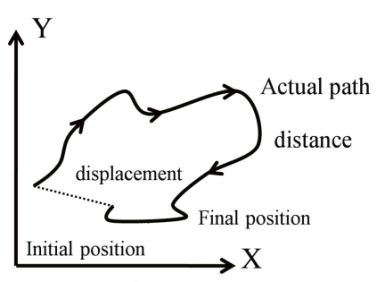
“length of actual path travelled by any object” It is scalar quantity so it will be always positive.
Distance ≥ Displacement
![]()
For straight line motion distance will equal to displacement.
UNDERSTANDING OF DISPLACEMENT AND DISTANCE
Example:-
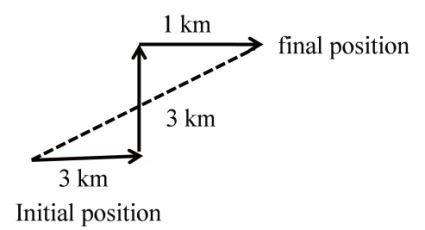
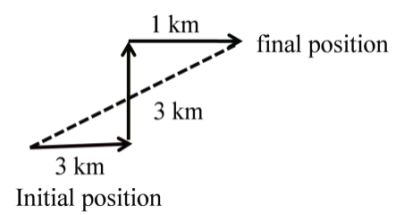
“A person is moving 3 km towards east then take left turn and move 3 km towards north then person take a right turn and move 1 km further due east and stops.
(i) What will be the total distance travelled by person.
(ii) What will be the net displacement of the person.
Solution: As we study in vectors and scalars.
(i) Distance: length of actual path so distance = 3 km + 3 km + 1 km = 7 km
(ii) Displacement: length of straight line
First method:
![]()
![]()
![]()
Second method
![]()
Applying Pythagoras = 5 km
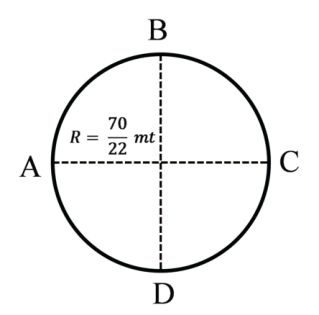
Example: 2 An object is moving in a circular path of radius of ![]()
meter shown in figure Find magnitude of distance
and displacement.
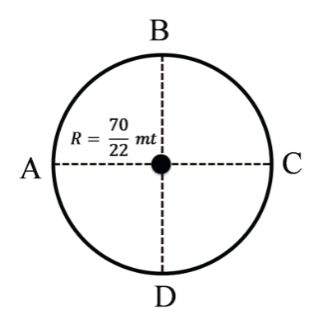
(i) From A to B
(ii) From A to C
(iii) From A to D
(iv) From A to A
Solution
A to B
![]()
![]()
![]()
= 5 meter
![]()
![]()
A to D
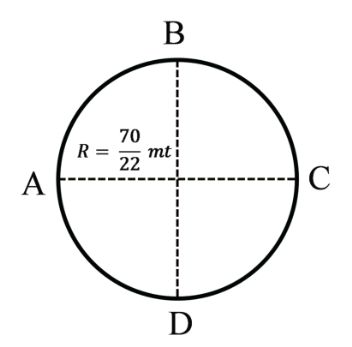
![]()
![]()
= 15 meter
![]()
![]()
A to C
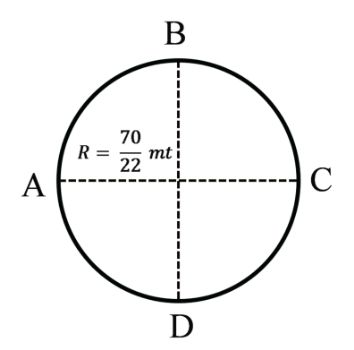
![]()
![]()
![]()
= 10 meter
![]()
![]()
A to A
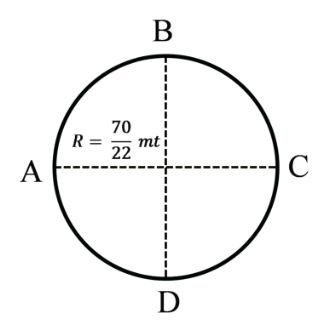
Distance = 2pR
![]()
= 20mt
Displacement = 0
1-D,2-D and 3-D motion, Trajectory(path) of projectile
1-D MOTION

2-D MOTION OR MOTION IN A PLANE Þ
Motion of any object in any of two axis involve (xy or yz or zx)
“Projectile Motion may be 2-D or even 3-D also but in general it is use to be 2-D Motion”
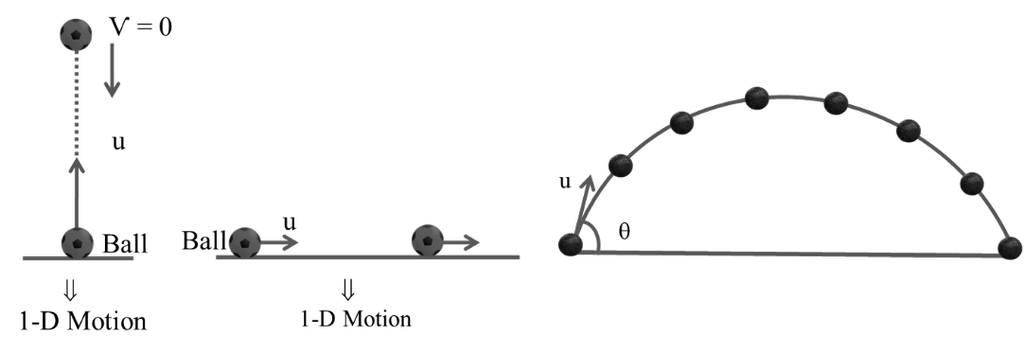
-D PROJECTILE MOTION

VERTICAL MIRROR

Vertical Mirror ® Gravity acts in vertical direction so we can use equations of motion
Time taken by the image of ball going up = time taken going down = t (Let)
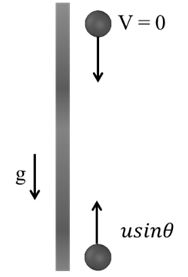
Use v = u – g t
O = u sinq - g t
Total time
![]()
![]()
Now to get Maximum height
Using v2 = u2 – 2g h
(O)2 = (usinq)2 – 2g H
![]()
HORIZONTAL MIRROR

Velocity remains constant so we can not use equation of Motion
Note: Untill any external reason present to change ucosq, like air flow ucosq remains Constant
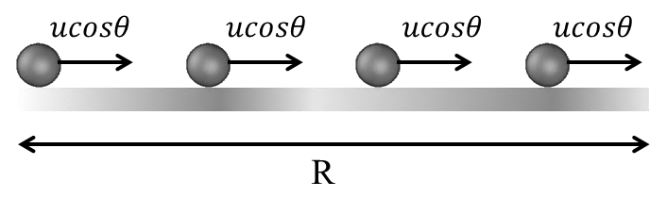
Now ucosq = Const
![]()
R = (u cosq) T
![]()
Now Sin2q = 2 sinq Cosq
![]()
Now we have
![]()
![]()
![]()
![]()
![]()
CONDITION
“These three results only when can be use if initial point of projection and final point of projection are at same level.
Example: A body of mass m is projected upward with initial velocity![]() then find time of flight, Maximum height attained and range attained by the body (g = 10m/s2)
then find time of flight, Maximum height attained and range attained by the body (g = 10m/s2)
Solution
![]()
![]()
![]()
![]()
![]()
![]()
Maximum range: To get maximum horizontal distance covered by any mass in projectile motion we must have a unique specified angle.
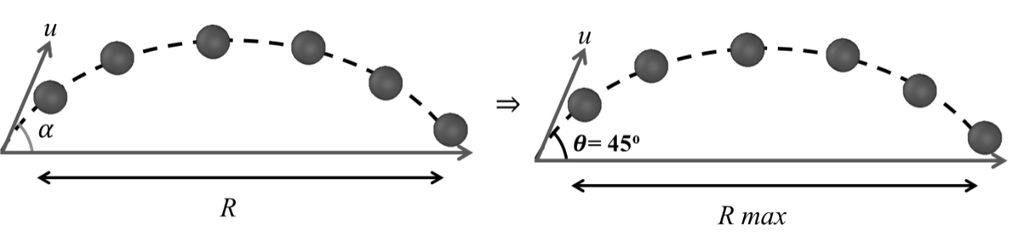
![]()
(Sin2q)max = 1
2q = 90°
q = 45°
To get maximum range angle of projection should be 45 °,![]()
![]()
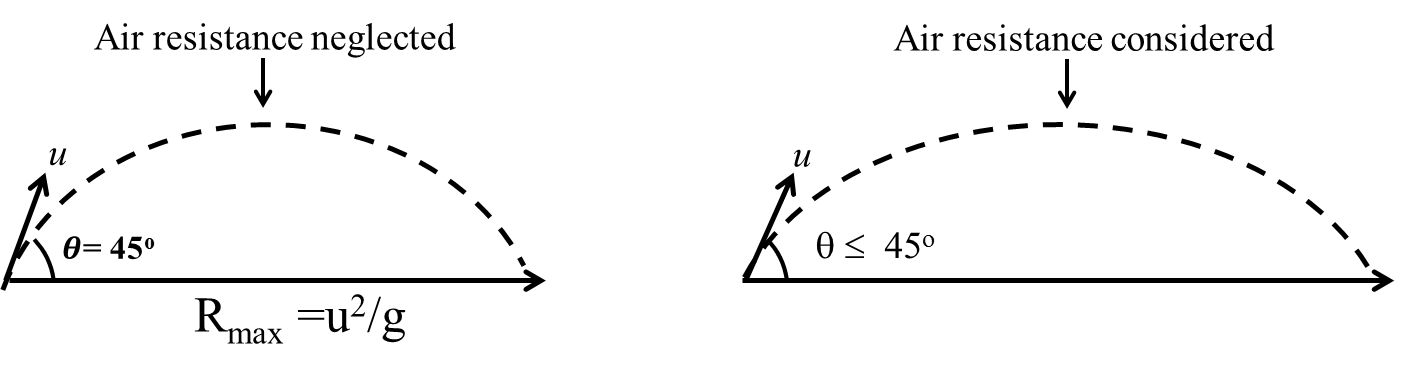
Note: Here we are neglecting the effect of air resistance. If we Consider air resistance then this angle q should be little bit less than 45°
SAME RANGE
Mathematically there must be two different angle of projection for which we will get same range
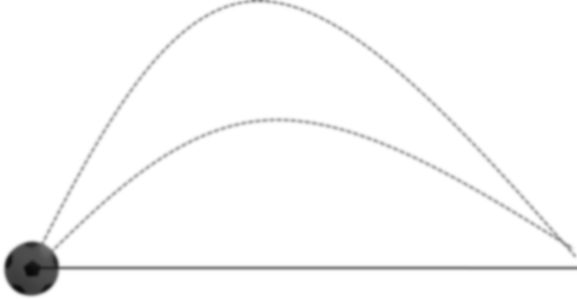
Ball 1
![]()
Ball 2
![]()
Now if we assume
a + b = 90°
then b = 90° - a
![]()
![]()
![]()
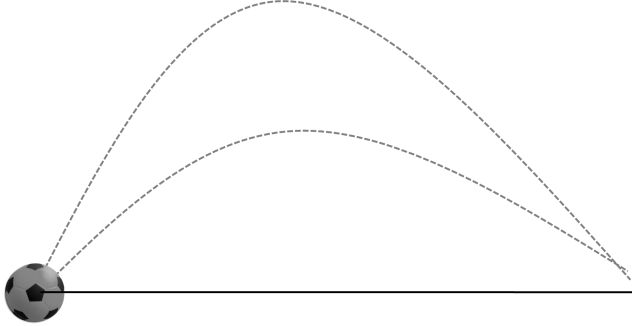
If sum of angle of projection is = 90° and initial speed is same then both balls will have same range.
Note: Here in this Case only range will be same not time of flight and maximum height
R1 = R2
T1 ¹ T2
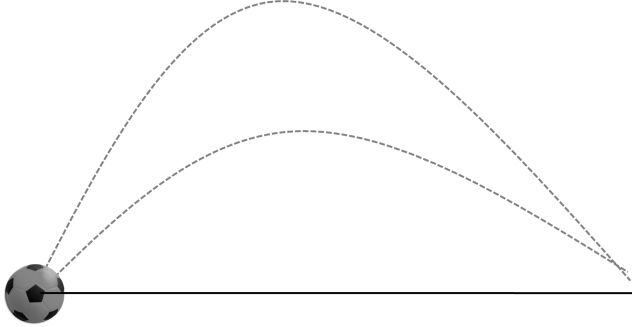
H1 ¹ H2
In case of same range relation of time of flights
Here we know a + b = 90°
Ball 1
![]()
Ball 2
![]()
![]()
![]()
Now
![]()
![]()
![]()
![]()
In case of same range relation of maximum heights
Here again a +b = 90°
Ball 1
![]()
Ball 2
![]()
=![]()
![]()
![]()
![]()
![]()
![]()
![]()
Relative motion
RELATIVE MOTION
Relative is a most common word use to compare any property of any object with respect to other object “
XAB = XA ─ XB,
↓
X of A with respect to B
Here x may be any physical or non physical quantity

Sign convention
![]()
VAB = VA - VB
= + 10 – (16)
VAB = - 6m/s , B says that it seems to be that car A is moving left with 6 m/s
But if VBA = VB - VA
= (16) – (+10)
VBA = 6m/s
A says that if seems to be that car B is moving right with 6 m/s
And if VBC = VB-VC
= (+16) – (-18)
= +34 m/s
C says that it seems to be that car B is moving right with 34 m/s
Also VCA = VC –VA
= - 18 – (+10)
= - 28 m/s
A says that it seems to be that car C is moving left with 28 m/s
Applications and Understanding of relative motion
Case : 1 Catching, collision problem
As shown in figure a cop is chasing to a thief . After how long the cop will catch the thief?
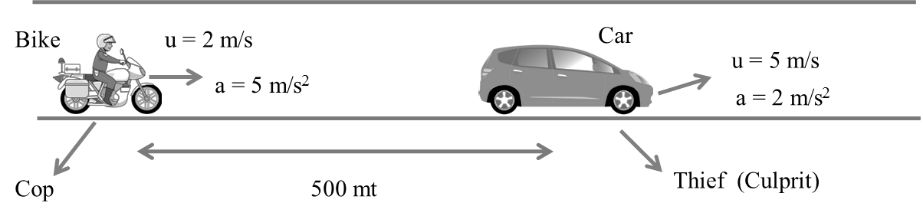
Solution : First of all we will shift our frame on car so now everything will be relative to car
Initial velocity of car w.r. to bike uCB = uC - uB
= 5 - 2
uCB = 3m/s
Acceleration of car w.r. to bike aCB = aC- aB
= 2 -5
= -3 m/s2
Distance of car w.r. to bike SCB = SC – SB
= 0 – 500
= - 500 mt
Note : Here we are shifting our frame on car so it would be at rest
![]()
![]()
![]()
![]()
![]()
Case II:- Lift or elevator in relative motion.
In this case it is given that boy is dropping a coin inside the lift at the same time lift also start moving down ward with acceleration 5 m/s2, if height of coin from the flower is 10 meter. Then find. Time after which coin strike the floor of lift.
Solution: Here again first of all we will shift our frame inside the lift (or on the lift).
So now lift is assume to be at rest now.
Initial velocity of coin w.r. to lift ucl = uc – ul
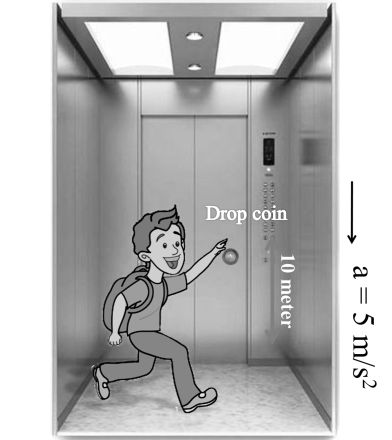
Because coins & lift start simultaneously = u – u = 0
Acceleration of coin w.r. to lift acl = ac – al
Sign convention = -g -5

= -10 -5
acl = -15m/s2
distance covered by coin w.r to lift hcl = hc –hl
= –10 – 0
= –10 meter
Now
![]() 5
5![]()
![]()
![]()
Circular motion,Vertical circular motion and Radius of curvature
If Any object moves such that it covers an angle q at the fixed point (center of the circle) and its gap from the fixed point remains constant (radius of the circle)
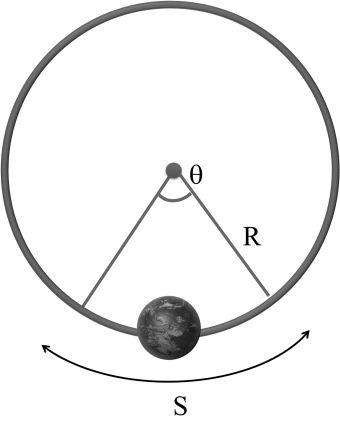
![]()
![]()
Here R is constants
![]()
![]()
Now finding linear speed of
(i) hour hand (30 cm)
(ii) Minute hand (90 cm)
(iii) Second hand (60 cm)
Solution:- (i) time period of hour hand T = 12 hr

= 12 x 3600 sec
v = r w
![]()
(ii) Minute hand:- time period = T = 60 min = 60 x 60 sec
![]()
(iii) Second hand:-
Time period= T = 60 sec
v = r w
![]()
Types of circular motion: (on the basis of speed)
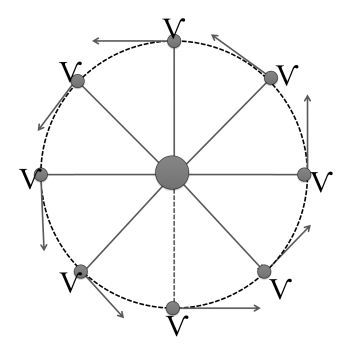
(1) Uniform circular motion: (U C M)
Only direction of velocity is changing, magnitude remains unchanged.
![]()
Now acceleration due to change in direction of velocity
![]()
Using law of parallelogram
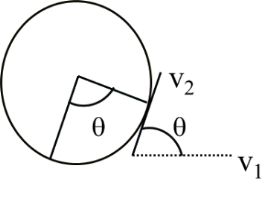
![]()
![]()
![]()
= 2v2 - 2v2 cosq
= 2v2 (1- cosq)
![]()
![]()
![]()
Now
![]()
![]()
sinq » q if q <<<<
![]()
![]()
a = v w,
![]()
![]()
![]()
Direction of this acceleration is towards center
![]()
Centripetal acceleration or Radial acceleration
(2) Non uniform circular motion (Non U C M)
Here in this case direction as well as magnitude both are changing continuously therefore here two different named acceleration will be as,
(i) ac = aR (centripetal or radial acceleration)
(ii) at (Tangential acceleration)
Now,
Tangential acceleration.
“Rate of change of magnitude of velocity”
v = R w
![]()
![]()
![]()
So at ^ ac
![]()
Net acceleration for non-uniform circular motion.
Example:- A particle moving in a circular path of radius 2 meter and its velocity varies as v = 10t2. Then net acceleration of the particle at t = 2 sec.
Solution: Given v = 10t2
![]()
= 20 x 2
= 40 m/s2
![]()
![]()
Centripetal force:- the force require to move in a circular path for any object with respect to inertial frame is called centripetal force.
![]()
Note:- Centrifugal force will also have same magnitude but direction opposite to centripetal force.
Direction of this force is towards the center.
HORIZONTAL CIRCULAR MOTION

(1) Only banking
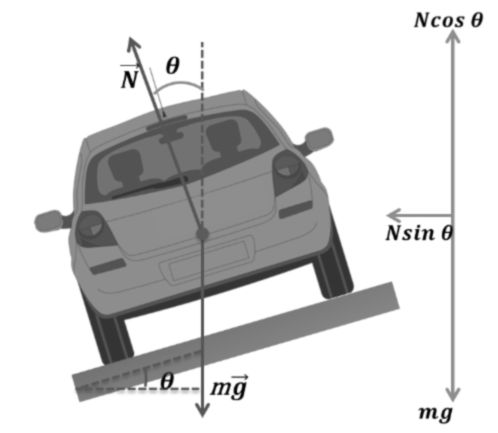
Here N sinq is C.P. provider
![]()
But N cosq = mg
![]()
![]()
Safe speed
(2) Only friction
Here now m N is C.P. provider

![]()
N = mg
![]()
![]()
![]()
Safe speed
Friction and Banking both:- To prevent inward sliding
cosq + m N sinq = mg
![]()
Divide
![]()
![]()

TO PREVENT OUTWARD SLIDING
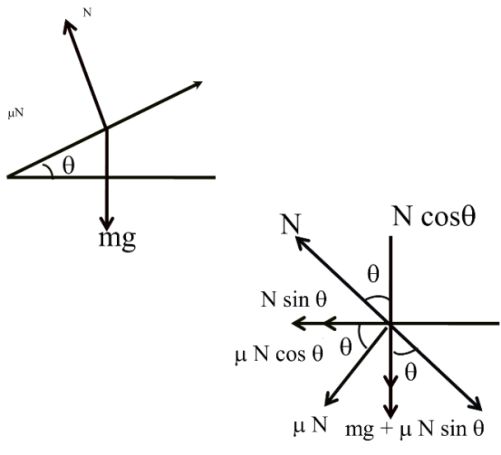
![]()
N cosq - m N sinq = mg
![]()
![]()
v1 < Vsafe < v2
![]()
CONICAL PENDULUM
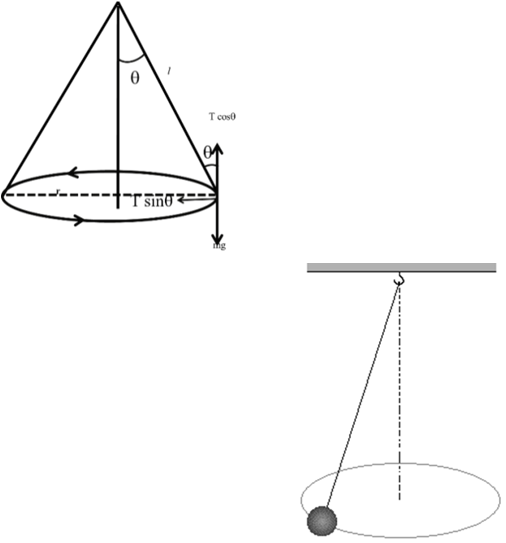
T sinq = mrw2
T cosq = mg
![]()
![]()
![]()
Time period of conical pendulum
![]()
![]()
![]()
![]()
Force, Constraint equation
Force:- Any pull or push”,![]() unit: kg met/sec2 or Newton (N)
unit: kg met/sec2 or Newton (N)
Types of forces:-
1- Field Forces:- No need of contact


![]() Always attraction type
Always attraction type
![]()
Direction:- Always along (-y) axis or straight vertically down ward.
(2). Contact forces: There must be some contact
(i) Normal force (N):- This force act when two surfaces of different object are in contact.
Direction:- perpendicular to contact surfaces.
(ii). Frictional force(f):- This force also act when two surfaces of different objects in contacts.
Direction:- Parallel to contact surfaces
Also F = m N here m is coefficient of friction.
Now
N → Perpendicular to contact surface
So F ^ N ![]()
![]()
Understanding of frictional force
The force which resist the motion”
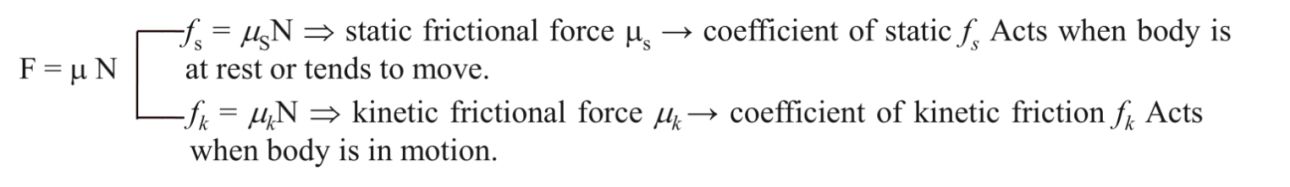
mS > mk m can be less than or greater than one
If Fext = 0, f = 0
![]()
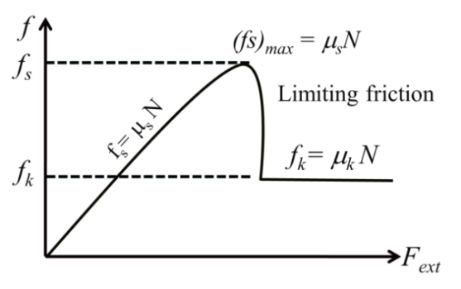
Example:- 1
Now
fs = msN
= ms mg
= 0.6 x 10 x 10
fs = 60 N
fk = mkN
= 0.2 x 10 x10
fk = 20 N
Amount of frictional force = 0
Because fext = 0, = f = 0
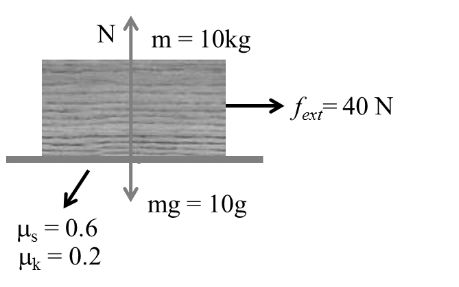
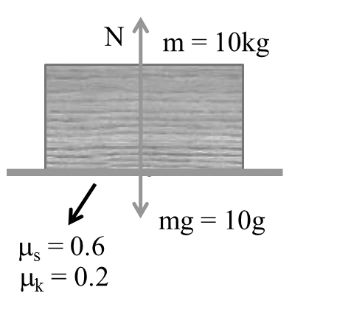
Example:- 2
m = 10 kg As in case (i) fs = 60 N, fk = 20 N
f = fs = 40 N
Body is at rest
Example:- 3
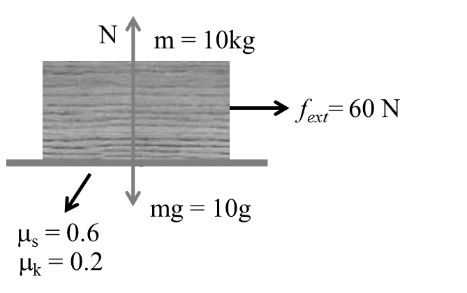
As in case (i) fs = 60N, fk = 20 N
f = fs = 60 = Fext → limitation friction
Body is at rest but tends to move
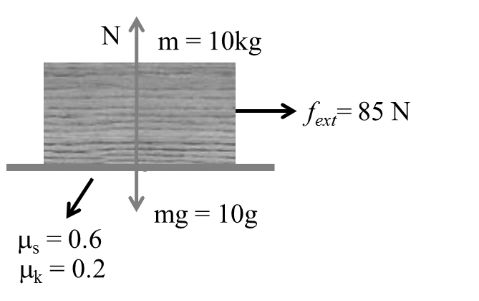
Example:- 4
As in case = fs = 60N, fk = 20N
Body is in moving condition
10a = 85 - 20
![]()
f = fk = 20 N
(3) Attachment forces indirect force
Direction: Direction of tension (T) is always away from the body.
Example:-
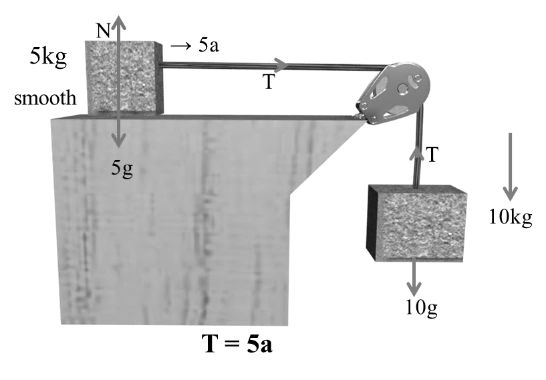
10 g –T = 10 a ---- (1)
N = 5 g ------(2)
T = 5a --------(3)
Solving 1& 310 g - 5a = 10a
15a = 10g
![]()
![]()
T = 5a
![]()
Net force on the pulley
![]()
![]()
Example:-
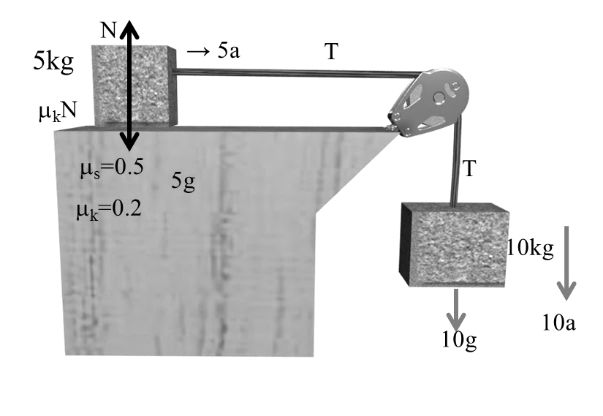
fs = ms N
= 0.5 x 5g
fs = 25 N
fk = mk N
= 0.2 x 5g
fk = 10 N
Pulling force for 5 kg
10 g = 100 N
So both block will move
10 g –T = 10a -----(1)
T -mkN = 5a ------(2)
T – 10 = 5a
N = 5g -----(3)
Solving (1) & (2)
10g –T = 10a
1-10 = 5a
90 = 15a Þ2![]()
Similarly
T -10 = 5 x 6 T= 40N
Work done,Kinetic energy and Conservative and non-conservative force
WORK DONE
(i) By Constant force
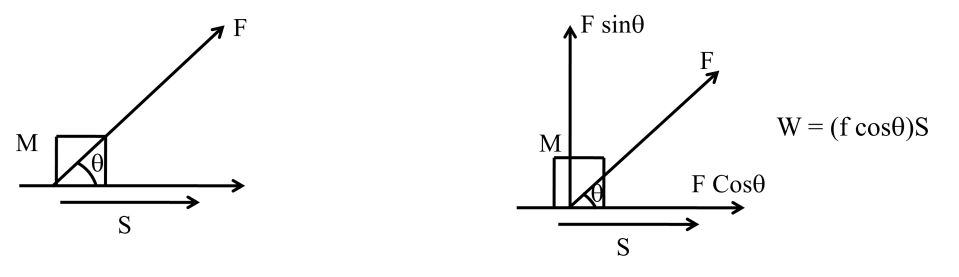
W = (f cosq) S
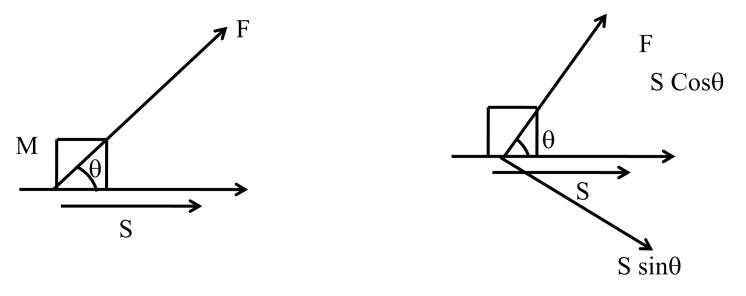
Work done by constant force = (force). (Displacement in direction of force
= (displacement). (force in direction of displacement)
 W=F.S
W=F.S![]()
W = FS Cos
Here W is Scalar but it may be +, ─, and zero
Work done will be equal to zero if
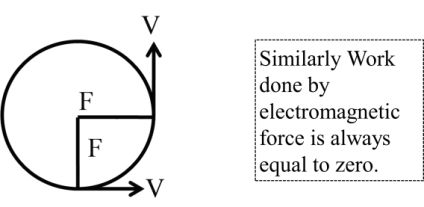
(i) Cosq = 0 = q = 90o = F ^ S or F ^ V
Ex. Work done by centripetal or centrifugal force is always zero.
Fm=q (V×B)![]()
Fm⊥V, Fm⊥B![]()
(2) Displacement = 0, S = 0 in circular motion
Negative work done
If cosq → negative, 180o ³ q ³ 90o
W → ─
Note: Work done by frictional force may be negative.
Example:- It is given that a particle is moving from initial position (2,3,5) to final position (4,1,2) under the action of constant force F=2i+3jN.![]() what will be the work done by the constant force.
what will be the work done by the constant force.
S��lution-Initial position r1=2i+3j+5K as given (2,3,5)![]()
Final position r2=4i+j+2k as given (4,1,2)![]()
Now S=r2-r1=2i-2j-3k![]()
F=2i+3j![]()
Now W=F.S.![]()
=2i+3j. (2i-2j-3k)![]()
= 4 -6 + 0.
W = -2j Ans
(ii) Work done by variable force
Case I: Applying integration force
W=F.dx=F.dy=F.ds![]()
or W= F.ds or W=F.ds![]()
Example:- if a variable force F depends on displacement X as F = (3x2 -5) due to this force body displaces from x = 2 mater to x = 5 meter find the work done by this variable force.
Solution: Given F = 3x2 – 5, displacement from x = 2 meter to x = 5 meter
W=25fdx=253x2-5dx ![]()
=3 25x2dx-525dx![]()
3x3325-5X25![]()
=33×53-23-55-2![]()
= [125 – 8] – 5 x 3
W = 102 J
Case II: Applying graphical method.
W = F.S if we have group F vs S then area under the S Curve will give us work done.
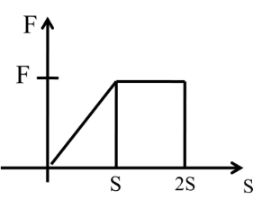 Work done = Area under the F – S curve
Work done = Area under the F – S curve
Area = 1/2 x basic height + length x width
= 1/2 x S x F + F x S
= 3/2 FS
W = 3/2 FS
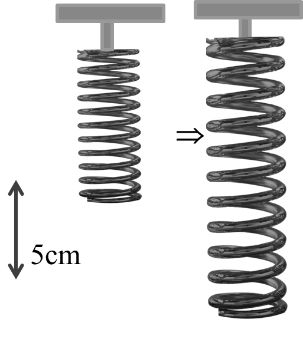 Example:- Spring force F = - Kx {Here K is Force constant} it a spring elongate by 5cm and force constant K is 100N/meter then find work done on stretching the spring.
Example:- Spring force F = - Kx {Here K is Force constant} it a spring elongate by 5cm and force constant K is 100N/meter then find work done on stretching the spring.
Solution:
Now F = -K x
= -100x
W=Fdx ![]()
=-10000.05xdx![]()
-100x2200.05![]()
-10020.052=-50×25×10-4![]()
= 1205 x 10-14
W = - 0.125 J Ans.
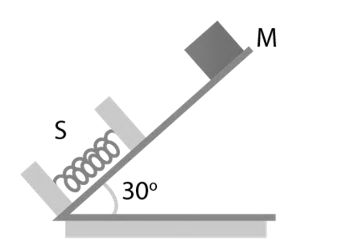 Question: An ideal massless spring S can be compressed 1 m by a force of 100 N in equilibrium. The same spring is placed at the bottom of a frictionless inclined at 30° to the horizontal. A 10 kg block M is released from rest at the top of the incline and brought to rest momentarily after compressing the spring by 2 m. If g = 10 ms-2, what is the speed of mass just before it leave the spring?
Question: An ideal massless spring S can be compressed 1 m by a force of 100 N in equilibrium. The same spring is placed at the bottom of a frictionless inclined at 30° to the horizontal. A 10 kg block M is released from rest at the top of the incline and brought to rest momentarily after compressing the spring by 2 m. If g = 10 ms-2, what is the speed of mass just before it leave the spring?
a 20 ms-1![]() b 30 ms-1
b 30 ms-1![]()
c10 ms-1![]() d 40 ms-1
d 40 ms-1![]()
Solution: F = kx
∴ k=Fx=1001![]()
= 100 N/m
Ei = Ef
∴12×10×v2=12×100×22-1010(2sin30°)![]()
Solving we get,
v=20 m/s![]() Answer (a)
Answer (a)
KINETIC ENERGY
Scalar quantity, always will be positive K = ½ mv2
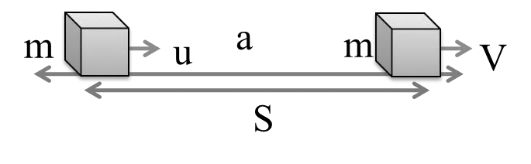 Work energy theorem: It is given that a mass is having initial velocity u accelerate and final velocity V and covered a distance S. Here v > u
Work energy theorem: It is given that a mass is having initial velocity u accelerate and final velocity V and covered a distance S. Here v > u
Initial kinetic energy K1=12mu2![]()
Final kinetic enrgy=K2=12mv2![]()
Using equation of motion
v2 = u2 + 2a s
12m v2-u2=2as12m ![]()
12mv2-12mu2=maS![]()
K2-K1 = FS
ΔK = W
Question: A body of mass m = 10-2 kg is moving in a medium and experiences a frictional force F = -kv2. Its initial speed is v0 = 10 ms-1. If after 10s, its energy is 18mv02,![]() the value of k will be (2017 JEE Main)
the value of k will be (2017 JEE Main)
(a) 10-3 kg-1 (b) 10-4 kgm-1
(c) 10-1 kgm-1s-1 (d) 10-3 kgm-1
Solution: Given, force, F=kv2![]()
∴Acceleration,a= -kmv2![]()
or dvdt= -kmv2![]()
⇒ dvv2= -km∙dt![]()
Now, with limits, we have
10vdvv2=-km0tdt ![]()
⇒ -1v10v=-kmt![]()
⇒ 1v=0.1+ktm![]()
⇒ v=10.1+ktm=10.1+1000k![]()
⇒ 12×m×v2=18×v02![]()
⇒v=v02=5![]()
⇒ 10.1+1000k=5![]()
Þ 1 = 0.5 + 5000 k
⇒ k=0.55000⇒k=10-4kg/m![]() Answer (b)
Answer (b)
Potential Energy: Scalar quantity may be +, - , Zero
Here F= -dUdrHere U is potential energy![]()
F.dr=-dU![]()
Note: if we find slope (tanq) of u –r graph then we will find amount of force.
BY THE U –R GRAPH
Slope at point A is positive
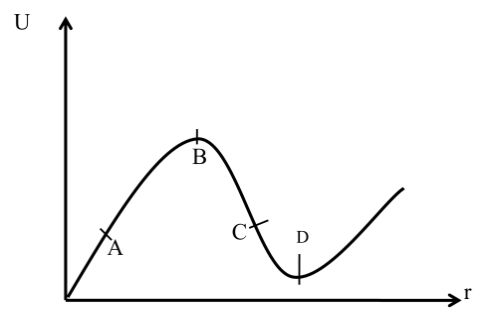 Slope at point B is zero here force at B will be zero similarly slope at C is negative slope at point D is zero.
Slope at point B is zero here force at B will be zero similarly slope at C is negative slope at point D is zero.
TYPES OF POTENTIAL ENERGY
(1) Elastic potential energy: Energy associated with state of Compression or expansion of an elastic object like spring. U = ½ kx2 Here x is the stretch of compression.
(2) Electric Potential energy: Energy associated with state of separation between charged particle
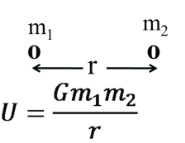 (3) Gravitational potential energy
(3) Gravitational potential energy
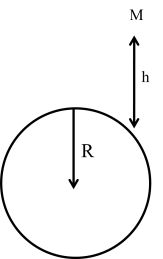 U=-Gm1m2r
U=-Gm1m2r![]()
Note: Attraction force the An U → negative always
U=mgh1+h/r![]()
If h <<<<< R
U = mgh
 Example: A chain is held on a frictionless table with (1/n)th of its length hanging over the edge if the chain has a length L and a mass M. how much work is required to pull the hanging part back on the table.
Example: A chain is held on a frictionless table with (1/n)th of its length hanging over the edge if the chain has a length L and a mass M. how much work is required to pull the hanging part back on the table.
amgl8n2![]() bmgl4n2
bmgl4n2![]()
cmgl2n2![]() dmgln2
dmgln2![]()
Solution: L length chain mass –M
I length chain mass –M/L
dy length chain mass MLdy![]()
W = DU
W=Mgl2n2![]()
du1 = (dm) gy
du1=MLg0l/nydy![]()
U1=mLgY220Ln=MLgL22n2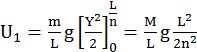
U1=MgL2n2,![]()
U2 = 0 at table
CONSERVATIVE AND NON-CONSERVATIVE FORCE
Conservative forces: Work done by conservative forces are independent of path. It only depends on initial and final position.
Ex:- Gravitational forces, electrostatic forces etc.
Note: Work done by conservative forces in closed path is always zero.
Wpath1 = W path2 = W path3
Non conservative force: Work done by non-conservative forces depends on path.
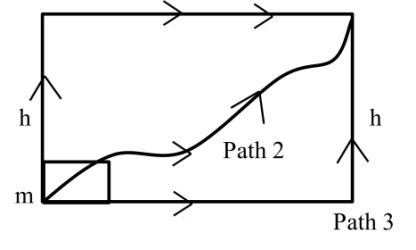 Ex:- frictional force, viscous force etc.
Ex:- frictional force, viscous force etc.
Power Work done per unit time P =F.V![]()
As we know W=∆K=∆U![]()
P=dwdt=w∆t=dkdt=dudt![]()
Unit. J/sec or watt
1 horse power = 746 watt.
CONSTANT POWER
Case I:- dependency of v on t.
Let an car of mass m accelerates staring from rest, while the engine supplies constant power P then how the V depends on t.
As we know P = Fv
P=mvdvdt![]()
Pdt=mvdv![]()
pt=mv22=V2=2ptm![]()
V=2Ptm=V∝t1/2![]()
Case II:- dependency of S on t
Let above result V=2ptm![]() `
`
dsdt=2Pmt![]()
0sds=2pmt dt![]()
S=2Pmt3/23/2 ![]()
S= 8P9m1/2 t3/2![]()
S∝t3/2![]()
Question: A uniform chain of length pr lies inside a smooth semicircular tube AB of radius r. assuming a slight disturbance to start the chain in motion, the velocity with which it will emerge from the end B of the tube will be
agr1+2π![]() b 2gr2π+π2
b 2gr2π+π2![]()
c gr π+2![]() d πgr
d πgr![]()
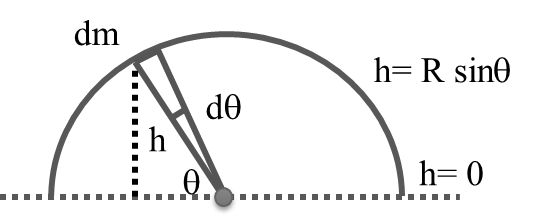 Solution: dm=mπ dθ
Solution: dm=mπ dθ![]()
∴ dU=dmgh= mπdθgrsinθ![]()
Ui= 0πdU=2mgrπ![]()
Now, Ki + Ui = Kf + Uf
∴ 0+2mgrπ=12mv2-mgπr2![]()
v=2gr 2π+π2![]() Answer (b)
Answer (b)
Newton's law of gravitation,gravitational potential, Keplar's law
NEWTON’S LAW OF GRAVITATION
![]()
![]()
Here G is universal gravitational Constant
G = 6.67 x 10-11 Nmt2/kg2
Dimensional formula = [M-1 L3 T-2]
Note: This formula is applicable for point mass only.
PROPERTIES OF GRAVITATIONAL FORCE
(1) It is always only attraction type force never repel.
(2) It is independent of medium between particles
(3) It is mutual force
![]()
![]()
(4) It is applicable for very far distant objects like interplanetary distance as well as for very short distance like inter-atomic distance
(5) It is conservative force means work done by this force is independent of path.
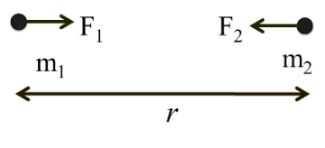
Example: Two particles of equal masses move in a Circle of radius r under the action of mutual gravitational attraction force. Then the speed of each particle if the mass of each particle is m .
![]()
![]()
![]()
![]()
Solutions:
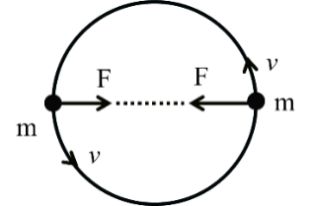
Here gravitational force F is centripetal force provider
![]()
![]() Answer (c)
Answer (c)
GRAVITATIONAL FIELD
Space of influence surrounding a mass m in which its gravitational effects are effective is called gravitational field of given mass.
Intensity of gravitational field due to point mass

GRAVITATIONAL FIELD OF EARTH HERE WE ARE ASSUMING
(1) Shape of earth is perfect sphere
(2) Center of mass of earth is at its center
(3) Uniform mass distribution
![]()
![]()
![]()
Intensity of earth gravitational field at its surface
Now here Eg = g we will use another term specially for earth is acceleration due to gravity Now At earth’s Surface![]() Direction of Eg or g is always towards the Center of earth Also weight of any object at the surface of earth W = F = m Eg = mg Force acting towards the center of earth Properties of ‘g’
Direction of Eg or g is always towards the Center of earth Also weight of any object at the surface of earth W = F = m Eg = mg Force acting towards the center of earth Properties of ‘g’
(1) It is independent of mass of any object
(2) It is not a universal constant its value depends on place, position and planet.
NOTE: For example value of g on the surface of moon is approximately g/6 i.e. 1/6 of the value on the earth
Variation of ‘g’
(1) Due to change of planet
As we know at the surface of earth
![]()
![]()
![]()
![]()
(2) Due to shape of earth
The earth is not perfectly spherical in shape but is on oblate sphere. It is bulged at the equator and flattened at the pole.
Equatorial radius is 21 km more than polar radius
![]()
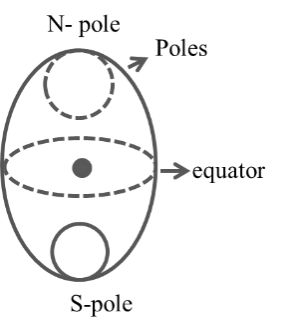
g ® Minimum at equator
g ® Maximum at poles
At the surface
gpoles > gequator
(3) DUE TO ROTATION OF EARTH
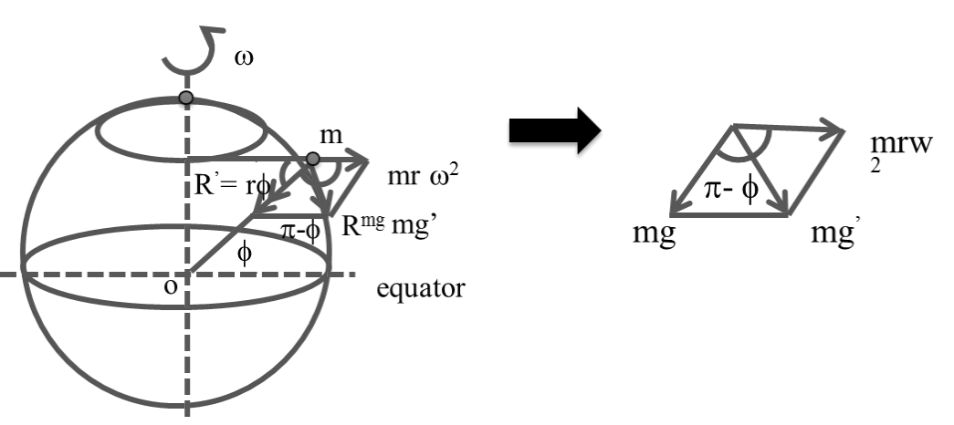
USING LAW OF PARALLELOGRAM
R2 = P2 + Q2 + 2 PQ cos a
(mg’)2 = (mg)2 + (mrw2)2 + 2 mg mrw2 cos (p - ϕ)
![]()
![]()
![]()
![]()
![]()
![]()
At the equator f= 0°
At the poles g’= g - Rw2
f = 90°, g1 = g – Rw2 cos2 90° g’ = g
4. At the depth h inside the earth
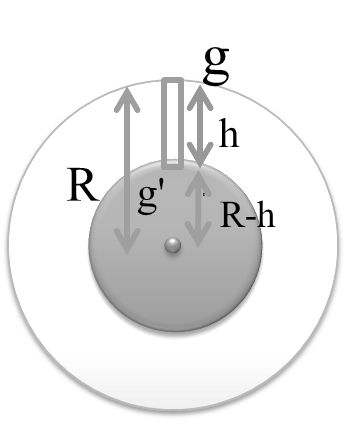
At the surface of earth
![]()
At depth h
![]()
Here
![]()
![]()
'![]()
![]()
![]()
At the Center of the earth
![]()
g’ = 0 weight less
5. At h height above the earth’s surface
At the surface of earth
![]()
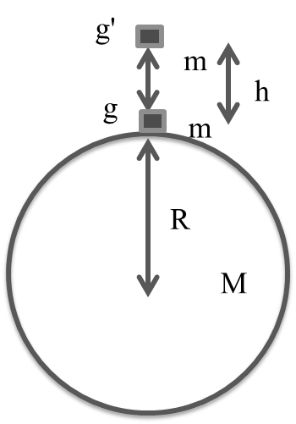
At the h height above
![]()
![]()
![]()
![]()
![]()
If h << R
Binomial expansion
(1+ x)n = 1+ nx
If x <<<<<<1
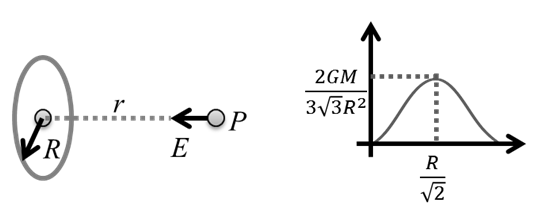
Field due to a Uniform Circular Ring at some Point on its Axis
Field strength at a point P on the axis of a circular ring of radius R and mass M is given by,
![]()
This is directed towards the center of the ring. It is zero at the center of the ring and maximum at ![]() (can be obtained by putting ).
(can be obtained by putting ).![]() Thus, E-r graph is as shown in the maximum value is
Thus, E-r graph is as shown in the maximum value is![]()
KEPLER’S LAW
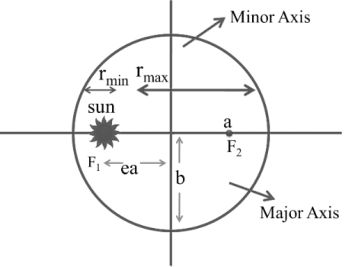
(1) Law of orbit: Each planet moves around the sun in an
elliptical orbit with the sun at one of the foci.
Here e is eccentricity of an ellipse
![]()
![]()
![]()
(2) LAW OF AREA
The line joining the sun and planet sweeps out equal area in equal interval of time.
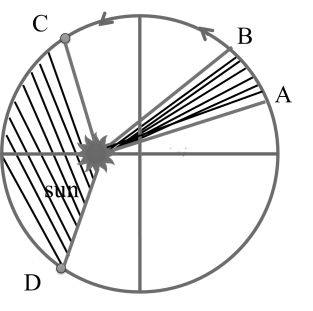
![]()
![]()
Here L = angular momentum of planet about the sun
(3) LAW OF PERIODS
Square of time period µ cube of semi major axis of elliptical orbit.
![]()
Final Touch Points
Polar and Geostationary Satellites
1. Satellites in low polar orbit pass over the poles. They orbit between 100 km and 200 km above the Earth’s surface, taking around 90 minutes to make each orbit. The earth spins beneath the satellites as it moves, so the satellite can scan the whole surface of the earth. Low orbit polar satellites have uses such as
- Monitoring the weather.
- Observing the earth’s surface.
- Military uses including spying.
2. Geostationary satellites have a different trajectory to polar satellites. They are in orbit above the equator from west to east. The height of their orbit-36,000 km is just the right distance so that it takes them one day (24 hours) to make each orbit. This means that they stay in a fixed position over the earth’s surface. A single geostationary satellite is on a line sight with about 40 percent of the earth’s surface. Three such satellites, each separated by 120 degrees of longitude, can provide coverage of the entire planet. Geostationary satellites have uses such as:
- Communications-including satellites phones
- Global positioning or GPS,
Geostationary satellites always appear in the same position when seen from the ground. This is why satellite television dishes can be bolted into one position and do not need to move.
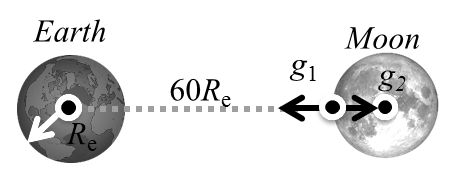
3. Acceleration due to moon’s gravity on moon’s surface is![]()
![]()
while acceleration due to earth’s gravity on moon’s surface is approximately .![]() This because distance of moon from the earth’s centre is approximately equal to 60 times the radius of earth and
This because distance of moon from the earth’s centre is approximately equal to 60 times the radius of earth and![]()
4. Total energy of a closed system is always negative. For example, energy of planet-sun, satellite-earth or electron-nucleus system is always negative..
5. If the law of force obeys the inverse square law ![]()
K=U2=E![]()
The same is true for electron-nucleus system because there also, the electrostatic force Fe∝1r2.![]()
6. Trajectory of a body projected from point A in the direction AB with different initial velocities:
Let a body projected from point A with velocity v in the direction AB. For different values of v the paths are different. Here, are the possible cases.
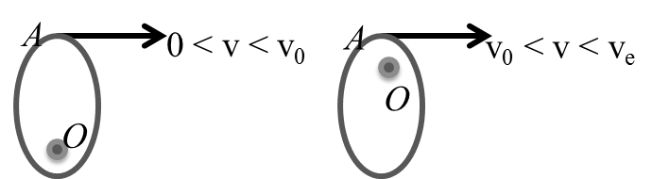
2. If v is not very large the elliptical orbit will intersect the earth and the body will fall back to earth.
![]()
![]()
![]()
![]()
![]()
(i) If times period of rotation of earth becomes 84.6 min, effective value of g on equator becomes zero or we feel weightlessness on equator.
(ii) Time period of a satellite close to earth’s surface is 84.6 min.
(iii) Time pendulum of a pendulum of infinite length is 84.6 min.
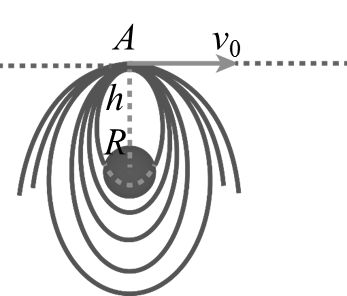
(iv) If a tunnel is dug along any chord of the earth and a particle is released from the surface of earth along this tunnel, them motion of this particle is simple harmonic and time period of this is also 84.6 min.
Note (a) Points (iii) and (iv) come in the chapter of simple harmonic motion.
(b) ![]() is also the time period of small oscillations of a block inside a smooth spherical bowl of radius R.
is also the time period of small oscillations of a block inside a smooth spherical bowl of radius R.
But this is not 84.6 min because here R is the radius of bowl not the radius of earth.
This expression can be compared with the time period of a pendulum.![]()
Moment of inertia of a single particle and rigid body,Radius of gyration,angular momentum
MOMENT OF INERTIA OF A SINGLE PARTICLE

I = mr2
![]()
MOMENT OF INERTIA OF A RIGID BODY

![]()
Theorem on Moment of Inertia
Theorem of Parallel Axis
I = Icm +Mr2

Theorem of Perpendicular Axis
Moment of Inertia is independent of Mass depend on distribution of mass
![]()
![]()

Moment of inertia of some regular shaped rigid bodies
![]()

![]()

![]()
![]()

![]()

![]()

![]()

RADIUS OF GYRATION
Let mass of the rigid body = M
Now I = S mr2
![]()
![]()
![]()
![]()
Here K is radius of gyration
RMS value of ![]()
Case I
A thin disc of mass M and radius R has mass per unit area![]() where r is the distance from its center. Its moment of inertia about an axis going through its center of mass and perpendicular to its plane is
where r is the distance from its center. Its moment of inertia about an axis going through its center of mass and perpendicular to its plane is
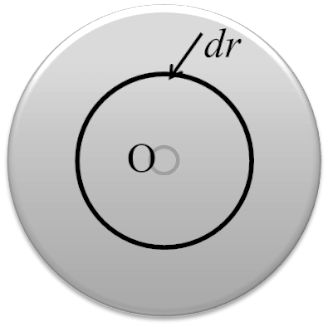
Given, surface mass density, ![]()
So, mass of the disc can be calculated by considering small element
of area 2prdr on it and then integration it for complete disc, i.e.
![]()
![]()
![]()
![]() ….(i)
….(i)
Moment of inertia about the axis of the disc,
![]()
![]()
![]()
Case II
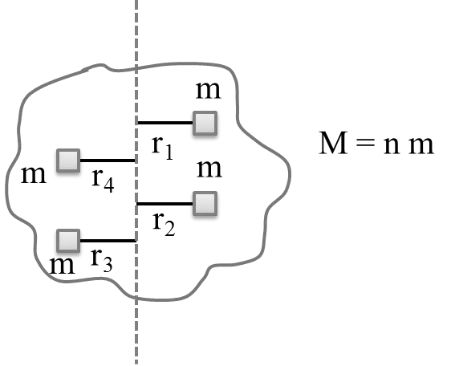
Two identical spherical balls of mass M and radius R each are suck on two ends of a rod of length 2R and mass M (see figure). The moment of inertia of the system about the axis passing perpendicularly through the center of the rod is Key idea This problem will be solved by applying parallel axis theorem, which states that moment of inertia of a rigid body about any axis is equals to its moment of inertia about a parallel axis through its center of mass plus the product of the mass of the body the square of the perpendicular distance between the axis.
We know that moment of inertia (MI) about the principle axis of the sphere is given by
![]()
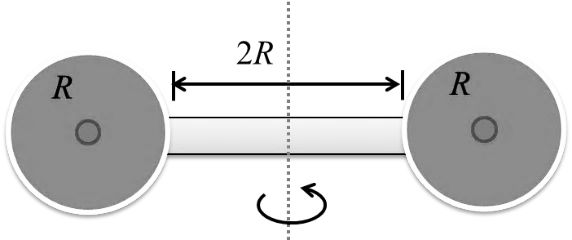
Using parallel axis theorem, moment of inertia about the given axis
![]()
![]()
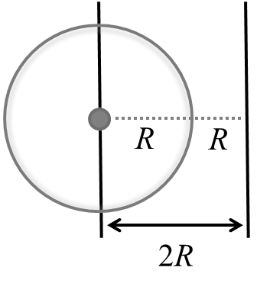
Considering both sphere at equal distance form the axis, moment of inertia due to both sphere about this axis will be
![]()
Now, moment of inertia of rod about its perpendicular bisector axis is given by
![]()
Here, given that
L = 2R
![]()
So, total moment of inertia of the system is
![]()
![]()
Case III
Seven identical circular planner discs, each of mass M and radius R are welded symmetrically The moment of inertia of the arrangement about an axis normal to the plane and passing through the point P is
From theorem of parallel axis,
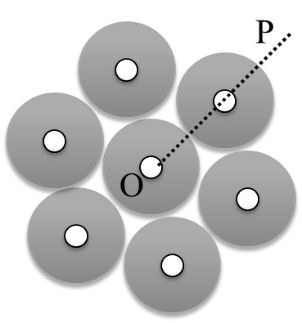
![]()
![]()
Case IV Cavity
Form a uniform circular disc of radius R and 9M, a small disc of radius ![]() is removed The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through center of disc is
is removed The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through center of disc is
![]()
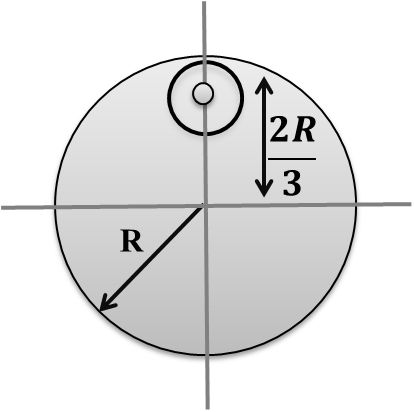
Case V
The moment of inertia of a uniform cylinder of length l and radius R about its perpendicular bisector is I. what is the ratio l/R such that the moment of inertia is minimum?

MI of a solid cylinder about its perpendicular bisector of length is
![]()
![]()
![]()
For I to be minimum,
![]()
![]()
![]()
![]()
![]()
![]()
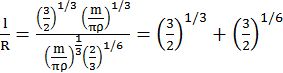
![]()
Case:- Moment of Inertia
Rod → mass = m, Length = L
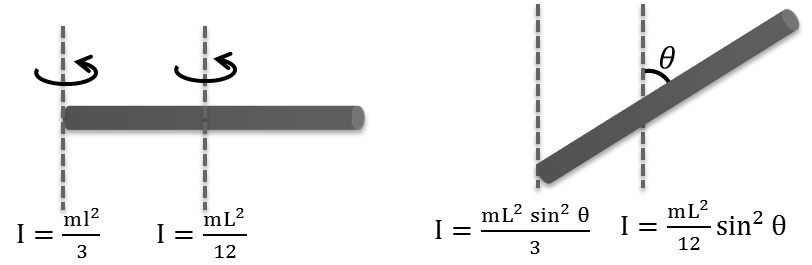
Disc → mass = m, Radius = R
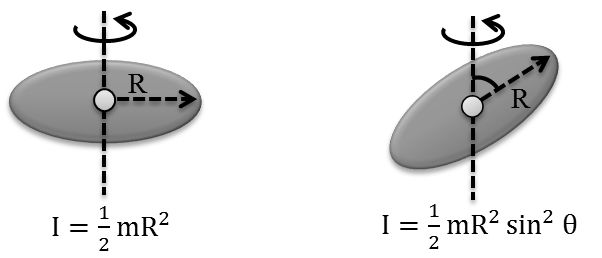
Multiple rods
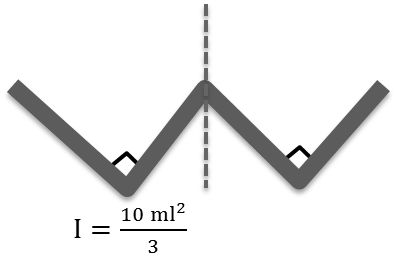
Each rod of mass m and length L
![]()
![]()
![]()
![]()
![]()
Torque of Force about the Axis of Rotation
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Case 1
A cylinder uniform rod of mass M and length l is pivoted at one end so that it can rotate in a vertical plane (see the figure). There is negligible friction at the pivot. The free end is held vertically above the pivot and then released. The angular acceleration of the rod when it makes an angle q with the vertical, is
As the rod rotates in vertical plane so a torque is acting on it, which is due to the vertical component of weight of rod.
Now, Torque t = force x perpendicular distance of line of action of force from axis of rotation
![]()
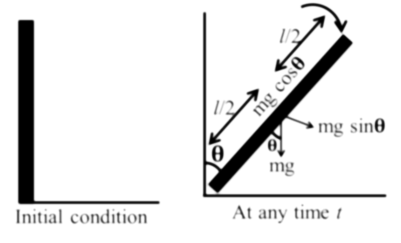
Again, Torque, t = Ia
Where, I = moment of inertia =![]()
[forced and Torque frequency along axis of rotation
passing through in end]
a = angular acceleration
![]()
![]()
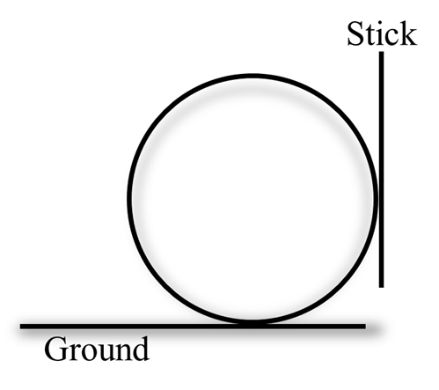
A boy is pushing a ring of mass 2 kg and radius 0.5 m with a stick as shown in the figure. The stick as shown in the figure of 2N on the ring rolls it without slipping with an acceleration of 0.3 m/s2. The coefficient of friction between the ground and the ring is large enough that rolling always occurs and the coefficient of friction between the stick and the rings is ![]() .
.
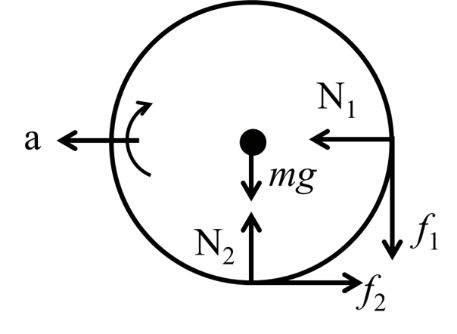
There is no slipping between ring and ground. Hence f2 is not maximum. But there is slipping between ring and stick. Therefore f1 is maximum. Now let us write the equations
![]()
![]()
![]()
![]()
![]()
![]()
Solving above four equations we get,![]()
Product of Vectors
![]()
![]()
![]()
Note: Vector triple product is not in our Physics syllabus.
SCALAR OR DOT PRODUCT
Product of magnitude of two Vectors with cosine of angle between them.
![]()
![]()
![]()
For perpendicular Vectors: ![]() ,q = 90° and cos 90° = 0
,q = 90° and cos 90° = 0 ![]()
![]()
![]()
![]()
![]()
Dot product of Standard unit Vectors:
![]()
![]()
![]()
![]() are mutually perpendicular then
are mutually perpendicular then
the value of m is
(a) - 2
(b) - 3
(c) + 3
(d) + 2
![]()
![]()
2 + m + 1 = 0
m = - 3 Answer (b)
Method to find dot or Scalar product
![]()
![]()
![]()
Finding Scalar and Vector Component (projection)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Component (projection) in the direction and in the perpendicular direction
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
vector or cross product
Product of magnitude of two Vectors with sine of angle between them.
![]()
![]()
For perpendicular Vectors:
![]()
For parallel Vectors:
![]()
![]()
![]()
For antiparallel Vectors:
![]()
![]()
![]()
Cross or Vector product of Standard unit vectors
![]()
![]()
USING RIGHT HAND SCREW RULE
![]()
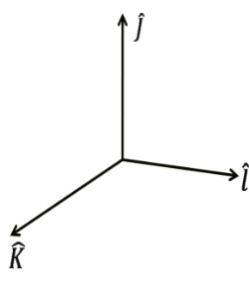
Method to find cross or vector product
![]()
![]()
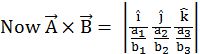
![]()
AREA OF TRIANGLE![]()
![]()
Area of parallelogram:
![]()
DIAGONAL OF PARALLELOGRAM
Example If the diagonals of a parallelogram are![]() and
and ![]() ,then area of this
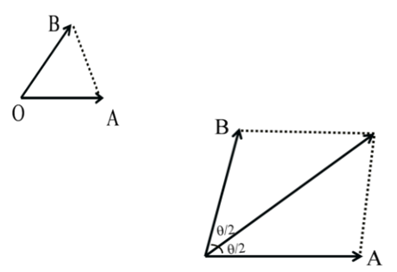
,then area of this
parallogram will be
(a) 2 unit2 (b) 3 unit2
(c) 4 unit2 (d) 1 unit2
![]()
![]()
![]()
![]()
![]()
= 2 unit2 Answer (a)
Example: Unit vector perpendicular to two vectors Finding a unit vector
perpendicular to
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Example: Consider three Vectors
Scalar triple product
![]()
![]()
![]()
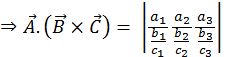
![]()
(a) 0
(b) 6
(c) 12
(d) 18
![]()
![]()
= 2 (3 n-2) -3 (15 + 1) -2 (10 + n) = 0
4n – 72 = 0
n = 18 Answer (d)
Velocity
VELOCITY
“Rate of change of displacement:
Vector so may be + , - , zero ,
Unit: meter/sec , km/hr , cm/sec etc
Dimensional formula: [LT-1]
![]() condition Þ Direction of velocity and displacement must be same
condition Þ Direction of velocity and displacement must be same
![]()
Example: There are four persons are standing at the four corners of a square. Assume that all four persons start with Constant
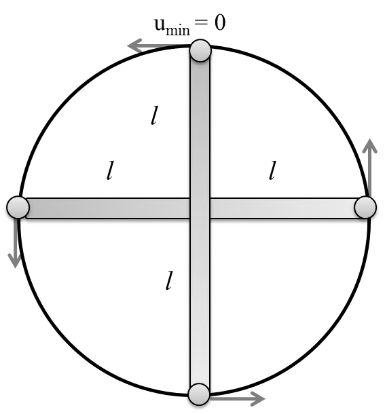
speed v and move towards each other. Find the time when all four persons will meet to each other. If length of each side is given l.
Solution:
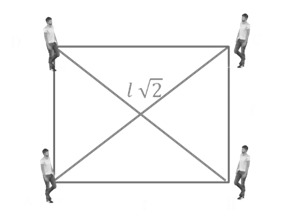
AC2 = AB2 + BC2
= l2 + l2
![]()
![]()
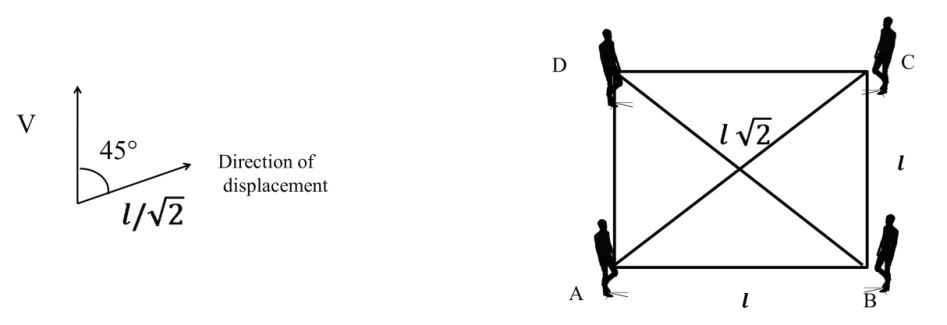
Now for person A direction of V
Component of v along direction of displacement is v ![]()
![]()
Note: General result for above Concept
Trick: If there is n person and polygon of n sides then time require to meet each other
![]()
Example. If there are 6 persons moving towards each other with Constant speed v. Initially all 6 persons standing at the Corner
of a hexagon then time required to meet
Solution: Use above result for general Case
![]()
![]()
Note: Similarly if there are three persons standing at the corners of a equilateral triangle.
![]()
MEAN OR AVERAGE VELOCITY
![]()
Case I Same time (S.T.)
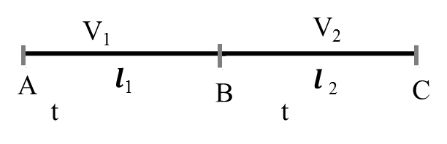
Now (Vav) AtoC = ?
![]()
![]()
![]()
![]()
![]()
As above
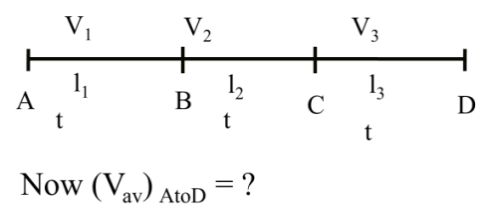
l1 = V1 t
l2 = V2t and l3 = V3 t
![]()
![]()
![]()
![]()
Case II Same gap (S. G.)
Now (Vav) AtoC = ?
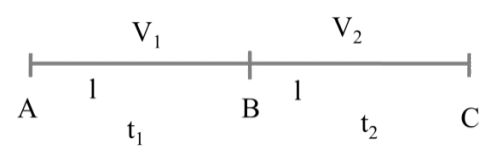
![]()
![]()
![]()
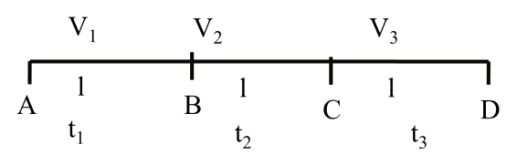
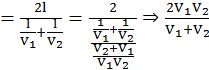
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Now Case I (S.T.) + Same gap (S.G.)
Example
Solution: Now for B to D Same gap
![]()
![]()
Acceleration:
“Rate of change of velocity
Vectors, so may be + , - , zero
Unit : met/sec2
Dimensional formula [LT-2],
![]()
Case I : Acceleration due to change in magnitude of velocity
If magnitude of velocity is increasing Þ

If magnitude of velocity is decreasing Þ

Retardation or Deceleration
Case II : Acceleration due to change in direction of velocity
![]()
![]()
![]()
![]()
![]()
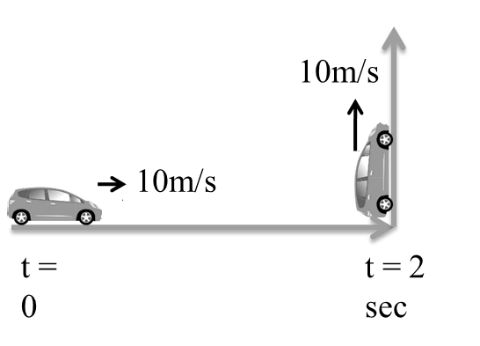
Example: A car is moving with 10 m/s due north after 2 second it take left turn and keep moving with 10m/s due west. Acceleration the Car will be
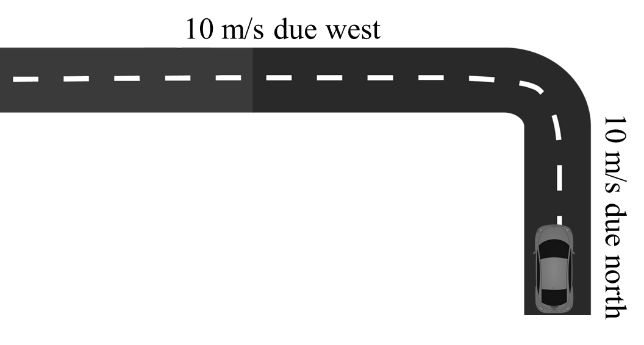
![]()
![]()
c 52m/s2 due S-E
d 52m/s2 due S-W
Solution:
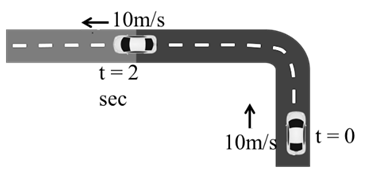
Initial velocity V1=10j m/s
Final Velocity V2=-10i m/s
Due North – West direction
a=V2-V1∆t
=-10i-10j2
a= -5i-5j
a=52 m/s2
Answer is (d)
For direction of acceleration
Ans 52 m/s2S-Wdirection
CONVERSION OF GRAPH
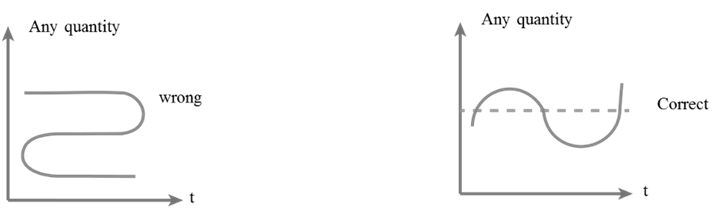
SOME IMPOSSIBLE (NON REALISTIC) GRAPH
(1) Distance never decrease

(2) Time never constant never decrease

(3) At a time no multiple values
Equation of Motion
Equation of Motion:
Condition: If acceleration is Constant
![]()
![]()
![]()
![]()
Motion Under Gravity
If any mass is throwing in air then a downward gravitational force mg acts on the mass and this type of motion is known as motion under gravity.
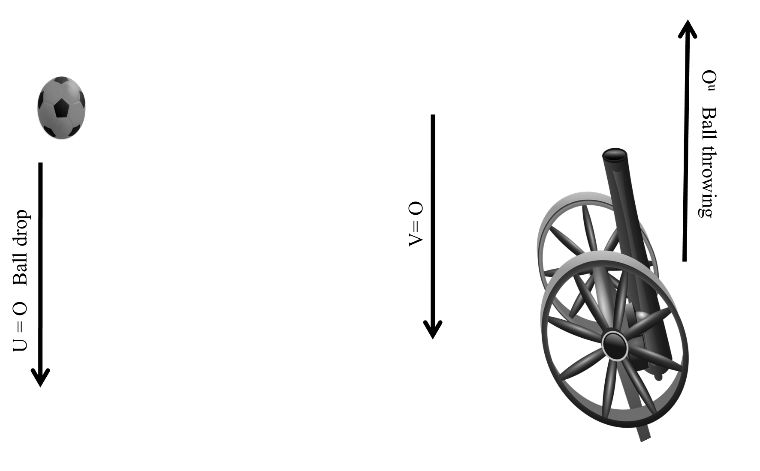
Case I:- When ball is dropping from the top equations of motion.
V = u + gt
![]()
v2 = u2 + 2 gh
Ball drops from any height then its initial velocity.
u = 0
Case II:- When ball is throwing upward with initial velocity u.
Equations of motion ,
v = u – gt
![]()
v2 = u2 – 2gh
At the top when ball reaches its maximum height then it final velocity.
V = 0
Important case (1) :-
When a ball thrown vertical upward with velocity u and it is said that distance covered by ball in tth sec is equal to (t + 1)th sec.
Þ It implied that final velocity of ball v becomes zero after time t.
Example:
If a ball is throw with initial velocity u and it distance travelled by the ball in 5th sec and 6th sec is equal then what will be the maximum height covered by the ball.
Solution:
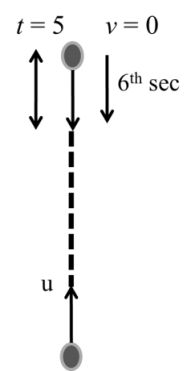
It is clear that time taken for upward motion of the ball is 5 sec there for down ward motion time will be 5 sec also.
For down ward motion
![]()
![]()
= 125 meter Ans
Important Case (2):-
If any object thrown vertically upward and it crosses certain height two time in a fixed interval of time.
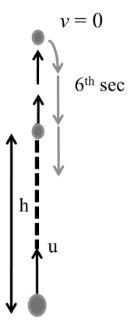
Example: A ball is thrown upward from the ground with an initial speed u. The ball is at a height of 80 meter at two times, the time interval being 6 sec. Find value of u.
Solution:-
Now,
![]()
![]()
5t2 –ut + 80 = 0
Now t must have two values t1 & t2
Using Sri Dharacharya
5t2 – ut + 80 = 0
Compare with ax2 + bx + c = 0
a = 5, b = - u, c = 80
![]()
![]()
Now t2 – t1 = 6
![]()
![]()
![]()
u2 -1600 = 900
u = 50m/s
Important Case (3):-
If any object starting from rest and moving with uniform acceleration has distance covered in equal interval of time will be in ratio of 1:3:5:7……….
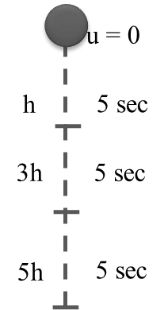
Example:-
If body drops from a certain height and it covers h distance in first 5sec then distance covered in next 5 sec also in further next 5 sec will be = ?
Solution:- fixed time interval is 5 sec by the ratio:-
For each 5 sec
h1 : h2 : h3 …. 1: 3: 5 : 7……
Important Case:- (4)
If a body starting from rest and moving with uniform acceleration then ratio of distance covered in 1sec, 2sec, 3sec….. = 1: 4 : 9: ….
= 12 : 22 : 32….. 42: 52
Important Case: (5): Juggler’s moving balls.
Example: A juggler keeps on moving four balls in the air throws the balls in regular interval of time. When one ball leaves his hand with speed 20m/s the position of other balls will be (g = 10m/s2).
Solution:-

V = u – gt
O = 20 – 10t
t = 2 sec for each ball to reach max
Now for ball 1
![]()
![]()
= 5 mt
From top so 15 mt from bottom
Maximum height
![]()
![]()
= 40 - 20
= 20 mt
Ball 1 is at 5 mt
5mt, 15mt, 20mt
Important Case (6):- Parachutist
Example: A parachutist after bailing out fells 50 meter without friction when parachute opens, it decelerates at 2m/s2. He reaches the ground with a speed of 3 m/s At what height did he bail out. (g = 9.8 ms2)
Important Case (6):- Parachutist
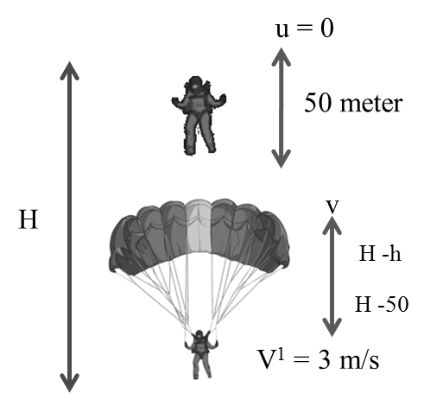
Example: A parachutist after bailing out tells 50 meter without friction when parachute opens, it decelerates at 2m/s2. He reaches the ground with a speed of 3 m/s At what height did he bail out. (g = 9.8 ms2)
Solution:-
V2 = u2 + 2 gh
V2 = 2 x 9.8 x 50
![]()
Now after parachute opens
V2 = V2 -2a (H – h)
9 = 980 – 2 x 2 (H - h)
4 (H - h) = 980 – 9
![]()
H = 242.75 + h = 242.75 + 50
≈ 293 mt. Ans
Important Case:- (7)
Ball drops from rising balloon.
Example:- A ball is dropped from a balloon going up at a speed of 7 m/s. If the balloon was at a height 60 met at the time of dropping the ball, how long will the ball take in reaching the ground
Solution:-
Using
![]()
Sigh convention

![]()
![]()
5t2 – 7t - 60 = 0
Compare ax2 + bx + c = 0
![]()
![]()
Taking + sigh
![]()
Graph of kinematics

Examples:-
(1) A body is moving with constant speed (v) and covers distance (s) in time (t)
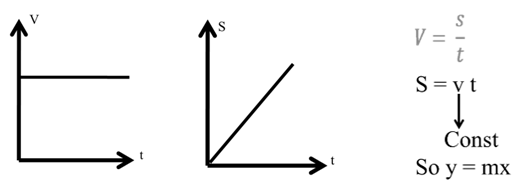
(2) A body starts from rest and moves with constant acceleration (a) attained velocity (Ѵ) and covers a displacement (s) in time t.

Ѵ = u + at
Ѵ = o + at
Ѵ = at
By y = mx
(3) A body is moving with speed u then accelerate with constant acceleration (a) and attain speed u as well as covered distance (s) in time t
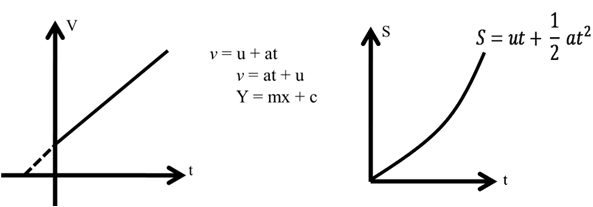
Example based on graph
A train starts from rest and moves with a constant acceleration of 2 m/s2 for half a minute. The breaks are then applied and trains comes to rest in one minute.
Find (i) Total distance moved by the train.
(ii) The maximum speed attained by the train
Solution: He we will draw V-t graph
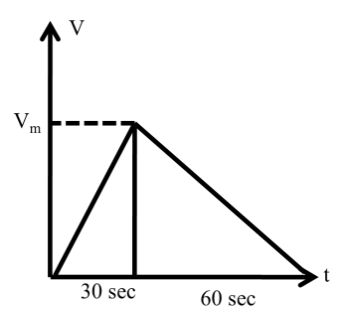
Now slope of V-t group Þ acceleration
![]()
Vmax = 60 m/s
to get total distance moved by the train we will get total area under the curve.
![]()
![]()
![]()
A1 + A2 = 2700 mt
= 2.7 km Ans.
Path of Projectile
TRAJECTORY (PATH) OF PROJECTILE
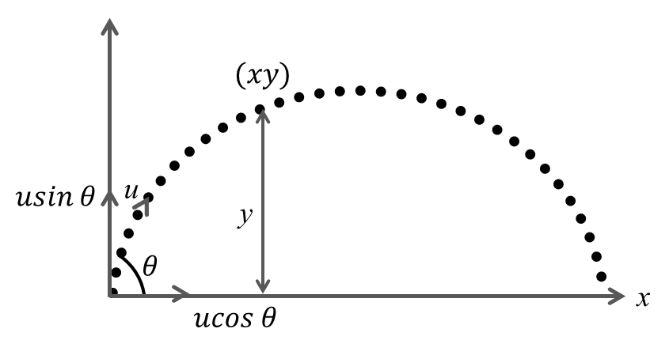
Along y- axis using
![]()
![]()
Along x-axis using
![]()
![]()
![]()
![]()
![]()
![]()
By this equation it can be prove that path of projectile is parabola
OTHER FORMA OF EQUATION OF TRAJECTORY
![]()
![]()
![]()
![]()
![]()
![]()
Projectile Motion when initial point and final point are at different level
Case I Horizontal projection from certain height
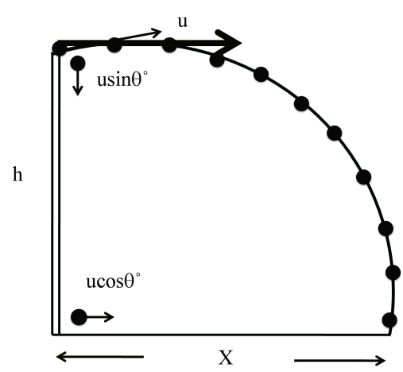
Here angle of projection q = 0˚
In vertical Mirror
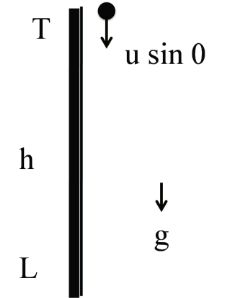
Using
![]()
![]()
![]()
![]()
Time to strike ground in horizontal Mirror
IN HORIZONTAL MIRROR
![]()
=![]()
![]()
Example: Which ball will strike the ground first
(a) Ball A (c) Ball C
(b) Ball B (d) All Balls will strike simultaneously
Solution
![]()
![]()
![]()
There fore all three Balls strike the ground simultaneously Answer (d)
Example: A jet fighter plane is flying at constant speed of 360 km/h and jet plane is moving horizontally at a height of 20 km from earth ‘s surface. Jet release a bomb to hit a target on the ground, how much horizontal gap before jet will release the bomb
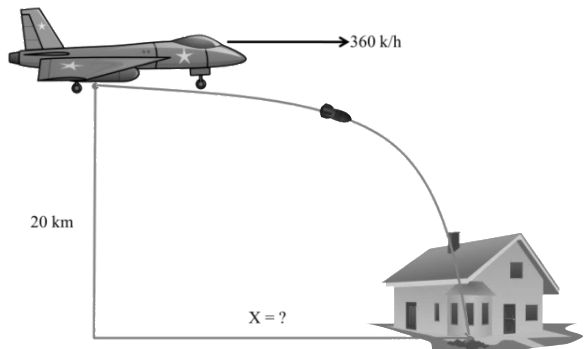
Solution
As discussed above using
![]()
![]()
![]()
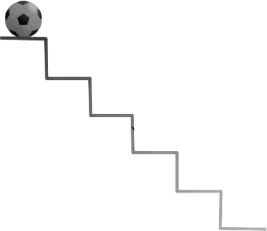
Example: A stair case having each step 10 cm high and 20 cm wide.
If a ball drops in horizontal direction from the top step with 10 mt/sec
in horizontal direction If ball strikes nth step of staire case find the n?
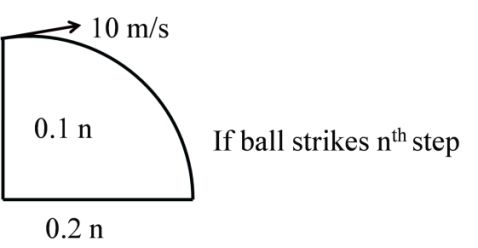
Solution
![]()
![]()
![]()
![]()
![]()
Now make a twist in above question
Every data is same except velocity of ball, if initial velocity not given , and saying what will be minimum initial velocity in above question so that ball hits 50th step
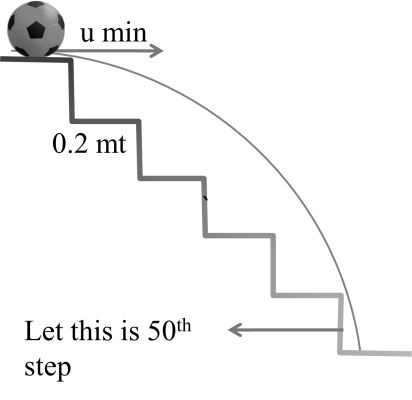
Solution
Now x = 49 x 0.2 mt
h = 49 x 0.1 mt
![]()
![]()
![]()
Projection in upwards and downwards directions
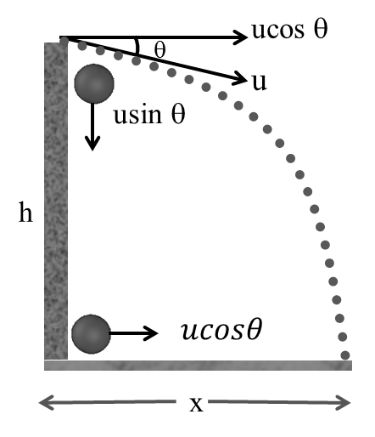
Case II Projection in upward direction with some angle with horizonta
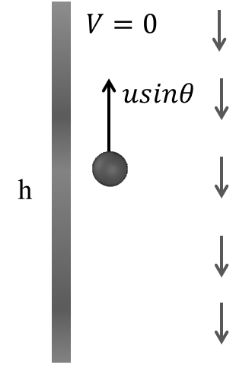
Vertical mirror
![]()
sign convention
![]()
![]()
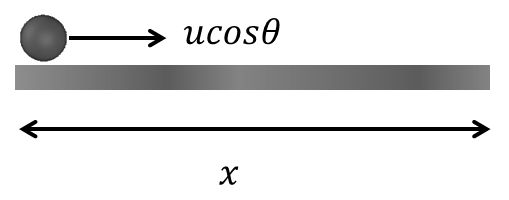
Horizontal Mirror
![]()
![]()
x = (u cosq) t
Case III Projection in downward direction with some angle with horizontal
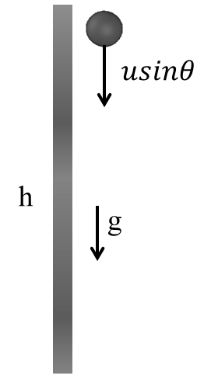
Vertical Mirror
![]()
![]()
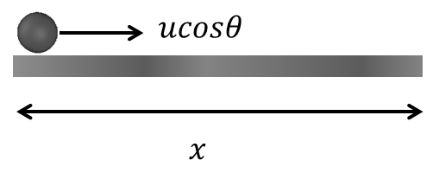
Horizontal Mirror
![]()
![]()
Projectile along inclined plane For Simplicity & understanding
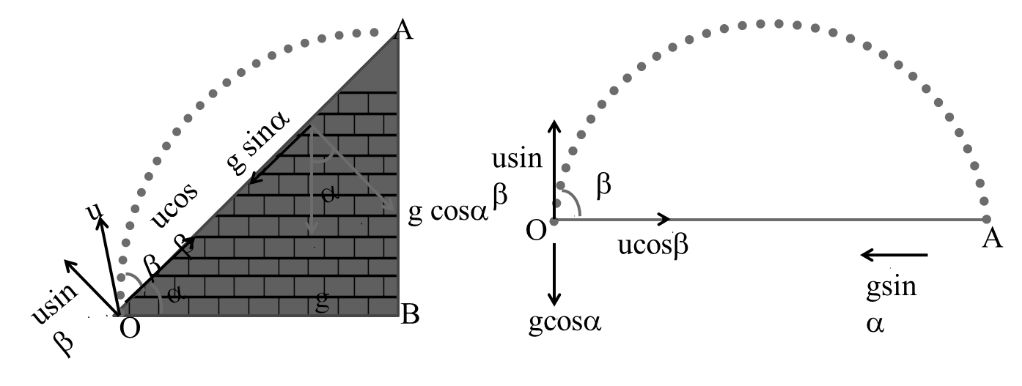
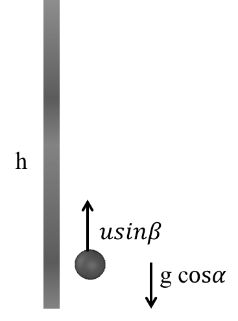
Vertical Mirror
V = u - g t
O = u sin b - (g cosa) t
![]()
![]()
Horizontal Mirror
![]()
![]()
OB = OA Cos a
Special case of Projectile Motion
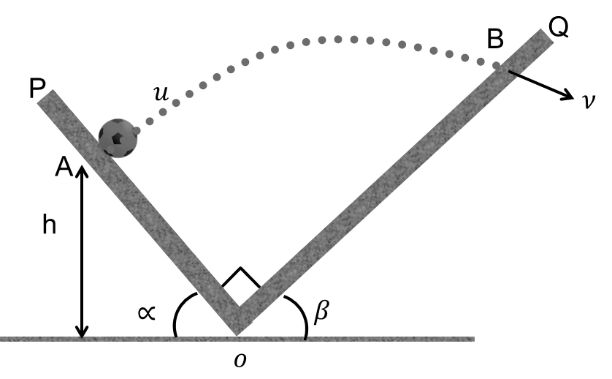
Case I
(i) Time of flight let OQ ® x -axis
OP ® y –axis
ux = u
uy = 0
ax = - g sin b
ay = - g cos b
Now
Vx = ux + axt
O = u – g sin bt
![]()
(ii) Final velocity V
Vy = uy + ay t
V = 0 – g cos b ![]()
V = u cot b
(iii) Height h ![]()
![]()
![]()
![]()
Now
h = Sy sin a
![]()
(iv) Distance AB
![]()
![]()
![]()
![]()
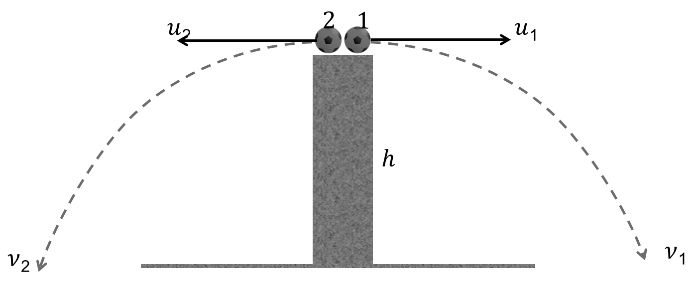
Now
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Case 2
(i) Time after which V1 ^ V2
Ball 1 ![]()
Ball 2 ![]()
Now ![]()
![]()
g2 t2 = u1 u2
![]()
(ii) gap between the ball 1 and ball 2 at the time ![]()
Ball 1 x1 = u1 t,
![]()
![]()
Ball 2
x2 = - u2t
![]()
![]()
Gap between Ball 1 and Ball 2
![]()
![]()
Gap = (u1 + u2) t
![]()
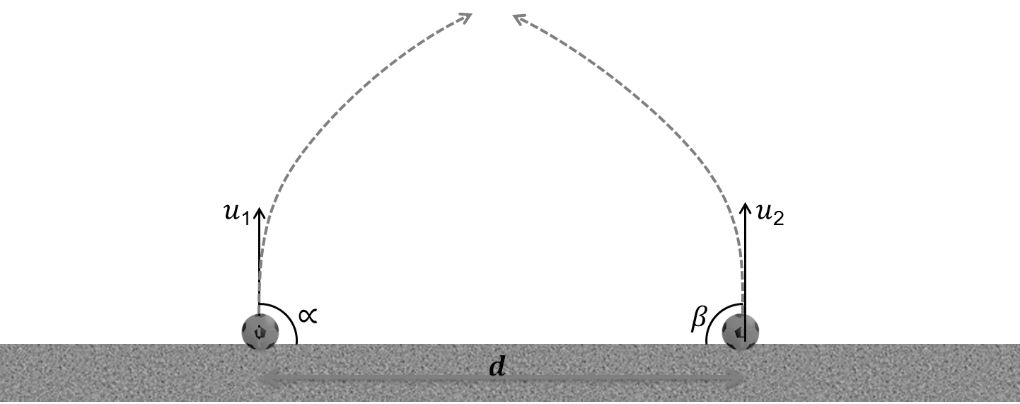
Case 3 Collision of two projectile
![]()
![]()
![]()
River Boat Problems
Case III:- River boat problems

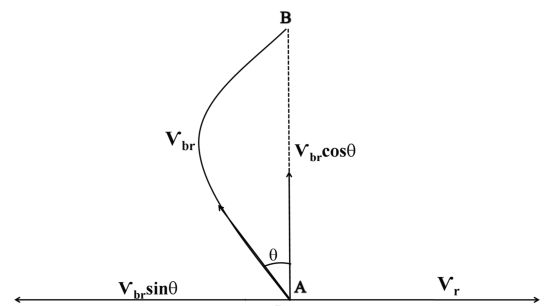
Now initially a boat or swimmer is at one bank of river (let say at point A) swimmer or boat man wants to cross the river and to reach the other bank of river by the concept of relative motion.
Vbr = = Vb – Vr
Vb = Vbr + Vr
Along y-axis (perpendicular to river flow)
(Vb)y = (Vbr)y + (Vr)y
(Vb)y = Vbr ![]() + 0
+ 0
Displacement along y-axis = d
Time taken to cross the river = t
![]()
![]()
Time take to cross the river ![]()
For minimum time or shortest time to cross the river
![]()
![]()
But in this case swimmer will not reach just opposite point he will cross the river and reach the other bank of river.

Drifting:- Horizontal distance due to river flow, when swimmer reach opposite bank of river. It is denoted by x
Now again Vbr = Vb - Vr
Along x –axis (Vbr)x = (Vb)x –(Vr)x
-Vbr sinq = (Vb)x –Vr
![]()
Disp. Along x-axis (Drifting) = x
![]()
![]()
![]()
Drifting in case of shorter time
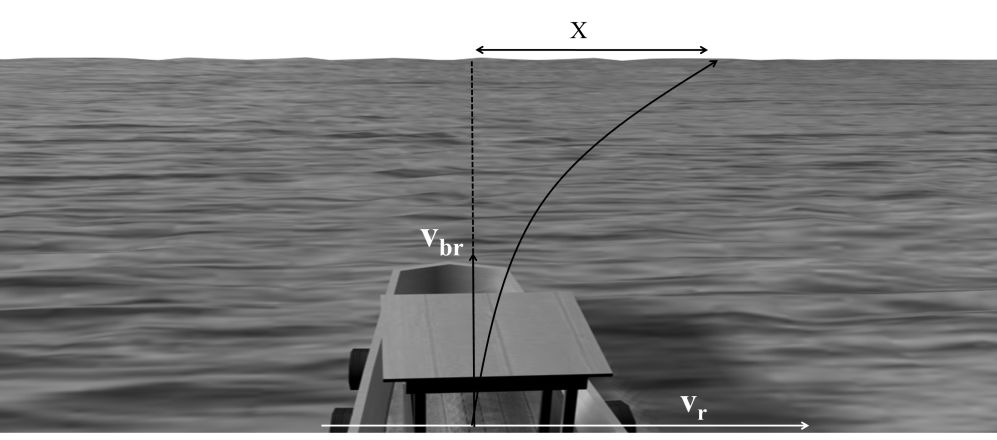
![]()
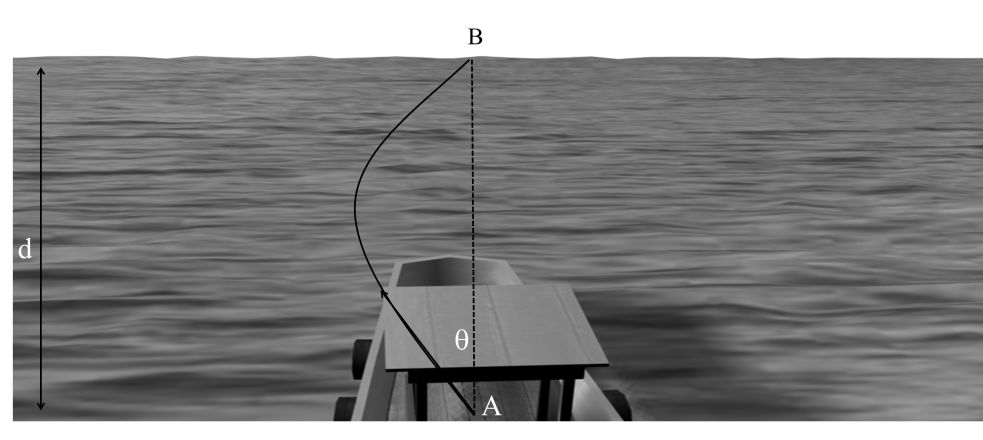
![]()
Drifting = 0
![]()
Vr – Vbr sinq = 0
![]()
Unique angle to reach just opposite point of the river
Now General value of time
![]()
![]()
![]()
Down the stream and up the stream
Down the stream
![]()
![]()
up the stream
![]()
![]()
Note: Above Case is also applicable in escalator or moving belt.
Example: A river is flowing due east with speed 3 km/hr. A boat is crossing the river with speed 5 km/hr with respect to still water. Fnd time taken by the boat if boat reaches just opposite point on the other bank of river. Given river width is 0.5 Km.
Solution. Vr = 3km/h
Vbr = 5 km/h
d = 0.5 km
Reaching just opposite point
![]()
Case:- 4 Rain and umbrella problems
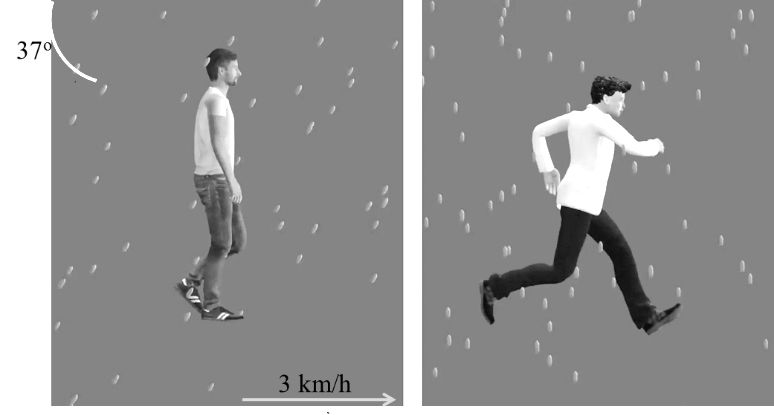
Case:- 4 Rain and umbrella problems
A person is moving with light walking speed of 3 km/h observe that rain is falling at angle of 37o with vertical if man increases his speed to 5 km/h he observe that rain is falling now in vertical direction. Find speed of rain with respect to ground.
Solution:-
Let velocity of rain is ![]()
Case I
![]()
![]()
![]()
![]()
![]()
![]()
![]()
3b = 4a-12
Case II:-
![]()
![]()
![]()
a = 5
Now 3b = 4a -12
3b = 4 x 5 - 12
![]()
![]()
![]()
![]()
Case I
A motorboat going downstream overcame a raft at a point A; t = 60 min later it turned back and after some time passed the raft at a distance l = 6.0 km below the point A. Find the velocity of the flow assuming that the engine worked in one regime in both directions .
Solution: Please see the video
Case 2
Two swimmers start swimming from point ‘A’ on one bank of the river to reach point ‘B’ lying right across on the other bank. One of them crosses the river along the straight line AB while the other swims at right angles to the stream and then walks the distances that the he has been carried away by the stream with velocity u to reach point ‘B’. Find at what value of u, both will reach point ‘B’ simultaneously? If the stream velocity is v0 = 2.0 km /h and velocity of each swimmer relative to the water is v’ = 2.5 km /h?
Solution: Please see the video
Case 3
An elevator car, whose floor – to –ceiling distance is 2.7m, starts ascending with constant acceleration a = 1.2 m/ s2; 2 s after the start a bolt starts falling from the ceiling of the car. Find the:
(a) bolt’s free fall time.
(b) Displacement and the distance covered by the bolt during the free fall in references frame fixed to the elevator shaft.
Solution: Please see the video
Vertical CM and String Mass
VERTICAL CIRCULAR MOTION
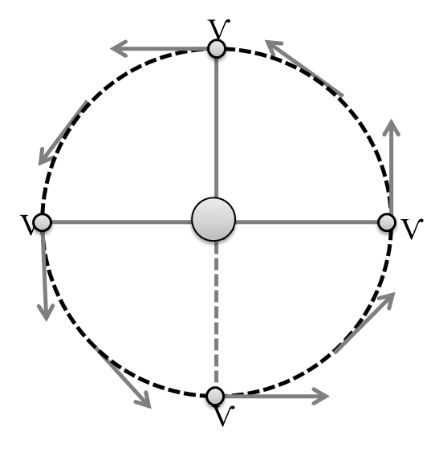
For top point
![]()
![]()
![]()
For middle position
v2 = u2 - 2gh
![]()
![]()
![]()
Tmin ≥ 3 mg
VERTICAL CIRCULAR MOTION
For Lowest point
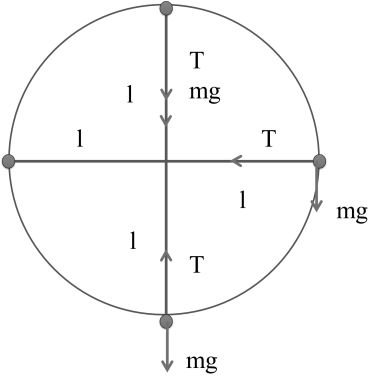
![]()
& Lowest to top
v2 = u2 – 2gh
![]()
![]()
![]()
![]()
Tmin ≥ 6 mg
STRING MASS SYSTEM
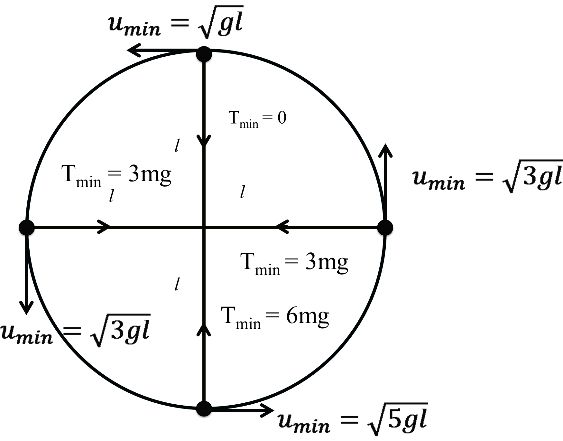
RIM & MASS SYSTEM
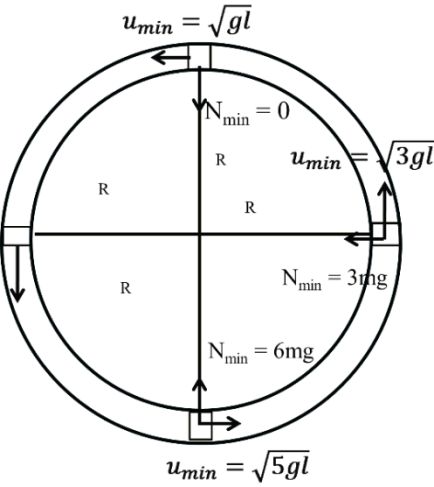
RIGID ROD AND MASS SYSTEM
To Complete the Circle if minimum velocity at top point = 0
![]()
Then Top to bottom
v2 = u2 - 2gh
(o)2 = u2 – 2g x 2l
![]()
At mid point
![]()
Lowest to mid point
![]()
v2 = u2 – 2gh
![]()
INCOMPLETE CIRCLE
Case I velocity given at lowest position
![]()
Case II velocity given at lowest point
![]()
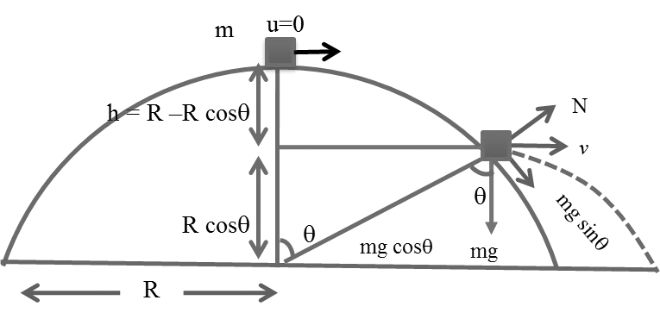
Example: As shown if figure a small mass m is put on the top of smooth hemisphere now this mass slightly hit to disturb it. At what angle it will leave the hemisphere.
![]()
Leaving the Circle so N = 0
![]()
![]()
Now from top to point where leave the Circle
v2 = u2 + 2gh
v2 = (0)2 + 2gR(1 - cosq)
gR cosq = 2gR (1 - cosq)
Cosq = 2 - 2 cosq
3 cosq = 2
![]()
![]()
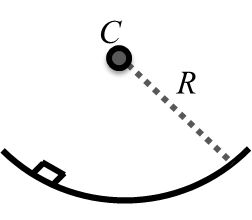
RADIUS OF CURVATURE
Case I At top of projectile motion
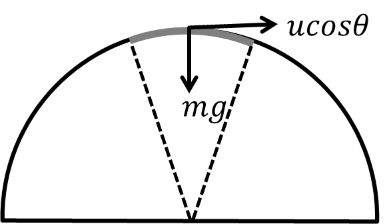
if we assume war the top point of projectile is a small Circular part then
![]()
![]()
Case II At any point before the top of projectile
At a point where velocity makes angle q/2 with horizontal
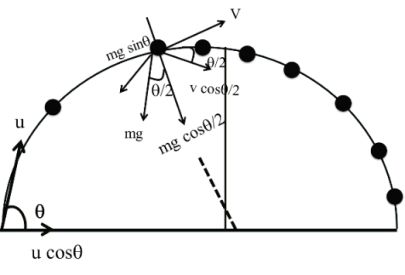
V cosq/2 = u cosq
![]()
![]()
![]()
![]()
Condition of toppling of a vehicle on circular tracks
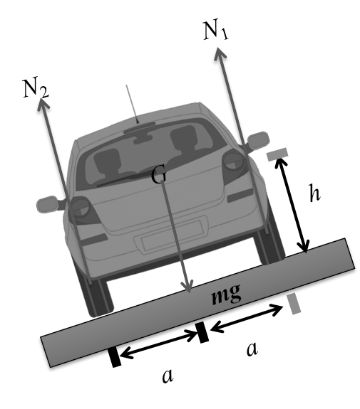
While moving in a circular track normal reaction on the outer wheels
(N1) is more than the normal reaction on inner wheels (N2).
Or N1 > N2
This can be proved as below.
Distance between two wheels = 2a
Height of centre of gravity of car from road = h
For translational equilibrium of car
N1 + N2 = mg … (i)
![]()
and for rotational equilibrium of car, net torque about centre of gravity should be zero.
Or N1 (a) = N2 (a) + f (h) … (iii)
From Eq. (iii), we can see that
![]()
Or N2 < N1
From Eq. (iv), we see that N2 decreases as v is increased.
In critical case, N2 = 0
and N1 = mg [From Eq. (i)]
N1 (a) = f (h) [From Eq. (iii)]
![]()
![]()
Therefore, for a safe turn without toppling![]()
From the above discussion, we can conclude while taking a turn on a level road there are two critical speeds, one is the maximum speed for sliding ![]() and another is maximum speed for toppling .
and another is maximum speed for toppling .![]() One should keep ones car’s speed less than both for neither to slide nor to overturn.
One should keep ones car’s speed less than both for neither to slide nor to overturn.
Case I
The length of each light rod is l. The mass of each small ball B and D is m. Balls are connected with a light smooth sleeve at point A as shown in the figure below. The frame is rotating with constant angular velocity w. A force F0 is
Question. If tension in AB wire is T1 and that in wire BC is T2. Then the value of (T2 – T1) is
(a) mg ![]()
(c) 2 mg dmg2![]()
Solution: At the ball B,
T2 sin 45° = mg + T1 sin 45° (in vertical direction)
T2-T1=mgsin45°=2 mg …(i)![]()
Question. The required force F0 on the sleeve is
![]()
![]()
(c) 2 mg ![]()
Solution: T1 cos 45° + T2 cos 45° = mrw2 (in horizontal direction)
![]()
or T1 + T2 = mlw2 …(ii)
From Eqs. (i) and (ii), we get
![]()
For bead, 2T1 cos 45° = F0
![]() Answer (a)
Answer (a)
Case II
A spherical ball of mass m is kept at the highest point in the space between two fixed, concentric spheres A and B (sec fig.) The smaller sphere A has a radius R and the space between the two spheres has a width d. The ball has a diameter very slightly less than d. All surfaces are frictionless. The ball is given a gentle push (towards the right in the figure). The angle made by the radius vector of the ball with the upward vertical is denoted byq. (2002 JEE Advance)
(a) Express the total normal reaction force exerted by the spheres on the ball as a function of angleq.
(b) Let NA and NB denote the magnitudes of the normal reaction forces on the ball exerted by the spheres A and B, respectively. Sketch the variations of NA and NB as function of cos q in the range 0 £ q £ p by drawing two separate graphs in your answer book, taking cos q on the horizontal axis.
Solution:![]()
Velocity of ball at angle q is
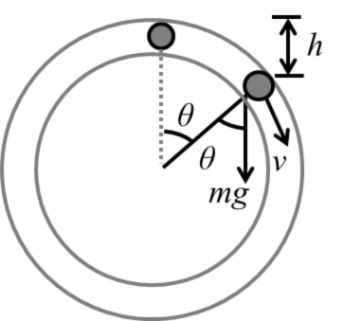
![]()
Let N be the normal reaction (away from centre) at angle q.
![]()
Substituting value of v2 from Eq. (i), we get
mg cos q - N = 2 mg (1 – cos q)’
N = mg (3 cos q -2)
(b) The ball will lose contact with the linner space when N = 0
![]()
After this it makes contact with cover sphere and normal reaction starts acting towards the centre.
![]()
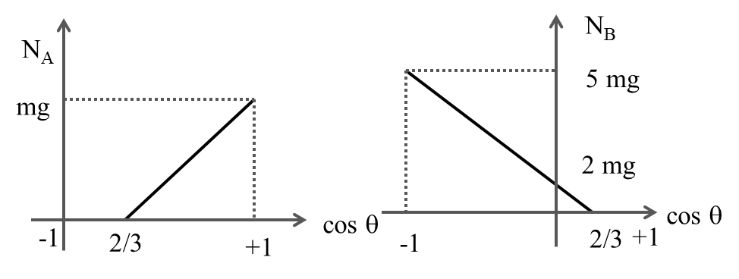
NB = 0
and NA = mg (3 cos q - 2)
![]()
NA = 0 and NB = mg (2 – 3 cosq)
The corresponding graphs are as follows.
Case III
A small smooth block of mass m is projected with speed ![]() from bottom of a fixed sphere of radius, R so that the block moves in a vertical circular path.
from bottom of a fixed sphere of radius, R so that the block moves in a vertical circular path.
Question. The speed of the block as function of q, the angle of deflection from the lowest vertical.
![]()
![]()
Solution: From free body diagram of the block, - mg sin q = mat
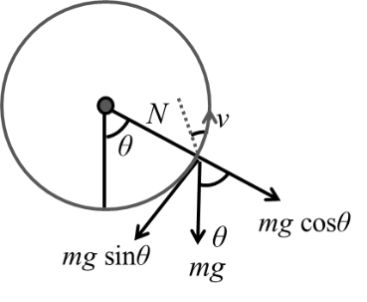
![]()
![]()
![]()
![]()
or v2 = 2gR – 2gR (1 – cos q)/
![]() Answer (b)
Answer (b)
Question. Normal reaction at the moment when vertical component of the block’s velocity is maximum.
(a) mg ![]()
![]() (d) 2 mg
(d) 2 mg
Solution: From the figure, vertical component of velocity is
![]()
![]()
![]()
![]()
![]()
![]() Answer (c)
Answer (c)
Question. The angle q between the thread and the lowest vertically at the moment when the total acceleration vector of the block is directed horizontally.
![]()
![]()
![]()
![]()
Solution: From the figure, the centripetal acceleration is ![]()
and a tangential acceleration is at = a cos q
or g sin q = a cos q
a = g tan q
![]() or v2 = gR tan q sin q
or v2 = gR tan q sin q
or 2gR cos q = gR tan q sin q
![]() Answer (c)
Answer (c)
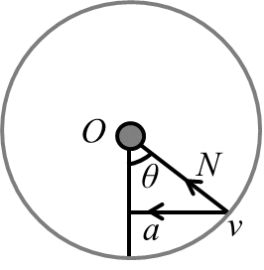
Constraint Equation
CONSTRAINT EQUATION
Here in place of constraint we will apply a trick
![]()
or T. a = coust.
Note: T a 1/v
![]()
10g –T = 70 a
7T -10g = 10a
70g -7T = 490 a
60g -500a
![]()
Constraint Equations
Simple Case
Conclusion
V1 = V2
a1 = -a2
x1 + x2 = l = const.
![]()
V1 + V2 = 0
![]()
a1 + a2 = 0
COMPLEX CASE

x1 + x3 = l1
(x1 – x3) + (x4 – x3) = l2
(x1 -x4) + (x2 –x4) = l3
![]()
V1 + V3 = 0
a1 + a3 = 0
a1 + a4 – 2a3 = 0
a1 + a2 – 2a4 = 0
Þ a2 = -7a1
SPECIAL CASE
![]()
![]()
![]()
![]()
V2 = V1 cos q
a2 = a1 cos q ![]()
W + Y + Z = l
![]()
![]()
![]()
![]()
V1 = V2 (1 + sin q)
PSUDO FORCE
T sinq = ma
T cosq = mg
![]()
Example Elevator or lift
T + 20 - 4g = 4a

6g – T - 30 = 6a
2g -10 = 10a
10 = 10a
![]()
T + 20 - 4g = 4 x1
T = 24N
Thrust on the pulley
F = 2T = 2 x 24 = 48 N
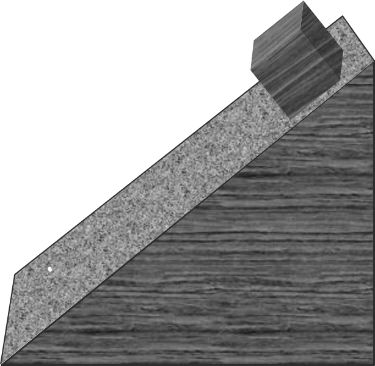
ROUGH INCLINED PLANE
![]()
![]()
N = 10g cos37o
fs = ms N
= 0.5 x 10 x 10 x 4/5
fs = 40 N
fk = mk N
= 0.3 x 10g cos37o
= 0.3 x 10x 10 x 4/5
![]()
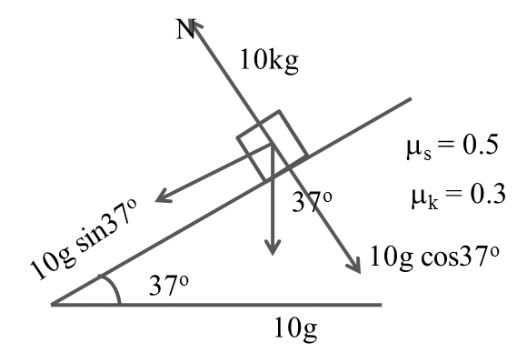
10 g sin 37o
= 10 x 10 x 3/5
= 60 N
Now Pulling Force > therefore block will move
So, 10g sin37o –fk = 10 a
10 x 10 x 3/5 – 24 = 10 a
Þ 10 a = 36
![]()
Center of Mass
Centre of mass
It is a point of a body or system at which the whole mass of body or system is supposed to be Concentrated for dealing its translation motion.
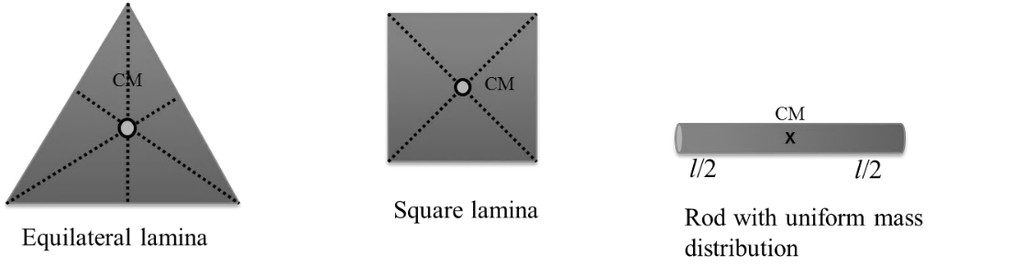
Properties of center of mass
(1) Three may or may not be any mass present physically at center of mass. So its position depends on shape of the body.
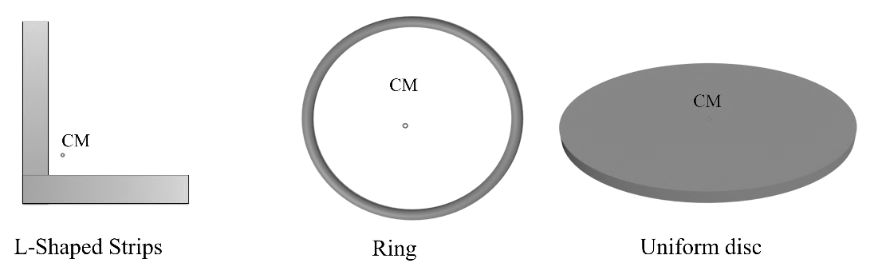
(2) For a given shape it depends on the distribution of mass within the body and is closer to massive part.

(3) If we apply the external force on cm then we will get maximum results
TO LOCATE CENTRE OF MASS
x- Coordinate of CM
![]()
y-Co-ordinate of CM
![]()
z-Co- ordinate of CM
![]()
Similarly in terms of position Vector
![]()
Example
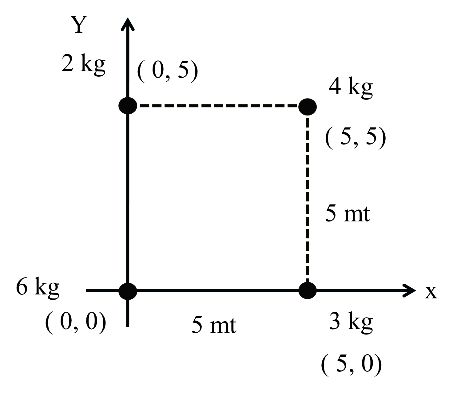
Step1. Choose your origin (try to fix your origin at extreme left and lower end)
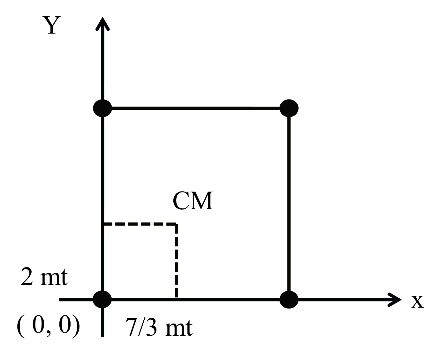
Step 2. Use above results e.g. xcm, ycm etc.
![]()
![]()
![]()
![]()
![]()
POSITION OF CENTRE OF MASS Arc of thin ring
![]()
0![]()
![]()
![]()
![]()
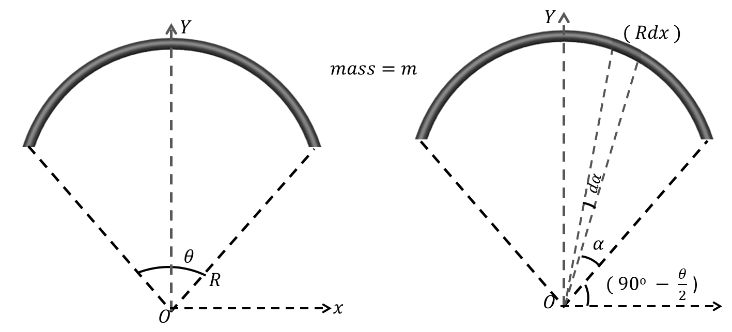
PART OF THE DISC
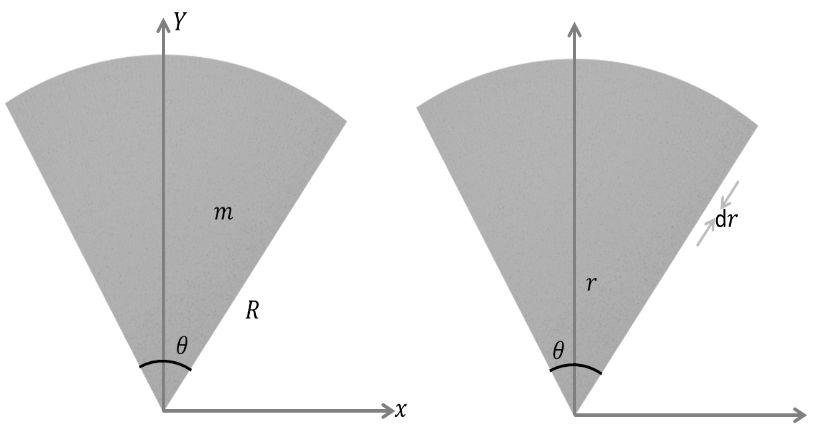
![]()
![]()
![]()
![]()
LOCATION OF C.M OF SOME HOMOGENEOUS RIGID BODIES
(1) Semi Circular ring
(2) Semi Circular disc
(3) Hollow hemisphere
(4) Solid hemisphere
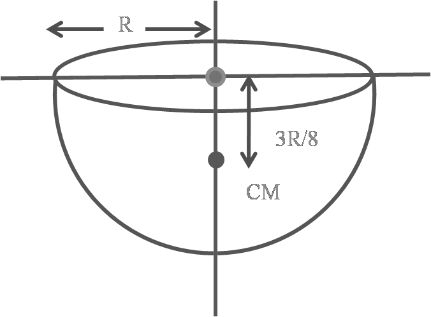
(5) Cone (Hollow)
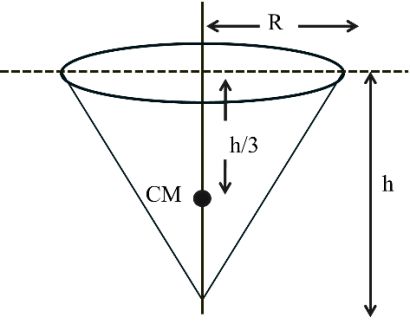
(6) Solid cone
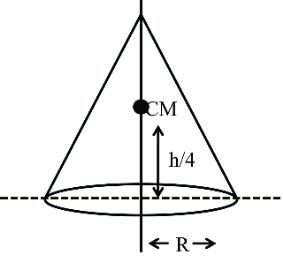
Concepts based on location of CM
CONCEPTS BASED ON LOCATION OF CM
Concept (1) Addition of masses
Given a small disc of radius R, thickness t is put over a large disc of same material and thickness, radius 2R- Finding C.M. of Combined System of two disc.
Step:- Fixed your Origin
![]()
![]()
Here ![]() is density and t is thickness so m α A
is density and t is thickness so m α A
![]()
Area of small disc = p(R)2 = pR2
![]()
![]()
![]()
Concept 2. Cutting of masses (Cavity)
In this case a small disc of radius R is cutting from a large disc of radius 2R. Now finding C.M. of remaining part of the disc
![]()
![]()
![]() So CM is located at left side form origin at distance R/3
So CM is located at left side form origin at distance R/3
Concep.3 Motion of CM
![]()
![]()
![]()
![]()
![]()
Concept 4. Shifting of C. M.
![]()
![]()
![]()
Example

Given if 2 kg block displace by 4 meter due right and 8 kg block displace by 2 meter due left then changing in position of C.M.
![]()
![]()
So C.M. will shift by 0.2 meter due left side
Example:
If 6 kg block moves towards down ward by 2 meter and if CM is to be Shift by +3 met in upward direction then amount and direction to which we have to shift 4 kg block.
D Ycm = + 3 mt
![]()
![]()
30 = - 12 + 4 DY2
Concept: 5 If Fext = 0 then C.M. will not move
Example: Given a boat of mass 50 kg is stationary on a lake. Two Person A and B are initially at two ends of the boat. Now both start to move towards each other and reach the center of the boat. So what will be the distance and direction boat will move.

Solution
![]()
![]()
![]()
![]()
(xcm)f = 7.5 mt,
Boat displace
(xcm)f – (xcm)i
= 7.5 - 6.5
= 1 met
Boat will move due left by 1 meter
Example: A trolley of mass 100 kg, length 10 mt along with a person of mass 50 kg is initially at rest. But now person moves towards other end of the trolley and reach to other end of the trolley. During this process distance with respect to ground moved by person and trolley. Here we are assuming that trolley is on the smooth surface.

Solution
![]()
![]()
![]()
![]()
Trolly will move by (xcm)f – (xcm)i
6.6 – 3.3
≈ 3.3 met due left side
CONCEPT .6 ACCELERATION OF CM
Example
Finding acm = ?
8g - T = 8a
T - 6g = 6 a
2g = 14 a
![]()
![]()
![]()
= -![]()
![]()
acm = - 0.2 m/s2
![]()
![]()
![]()
A uniform bar of length 12 L and mass 48 m is supported horizontally on two fixed smooth tables as shown in figure. A small moth (an insect) of mass 8m is sitting on end A of the rod and a spider (an insect) of mass 16 m is sitting on the other end. B. Both the insects moving towards each other along the rod with moving at speed 2v and then spider at half this speed (absolute). They met at appoint P on the rod and the spider eats the moth. After this the spider moves with a velocity ![]() relative the end A. The spider takes negligible time in eating on the other . Also, let
relative the end A. The spider takes negligible time in eating on the other . Also, let ![]() where T is a having value 4s.
where T is a having value 4s.
Question. Displacement of the rod by the time the insect meet the moth is
![]() (b) L
(b) L
![]() (d) zero
(d) zero
Solution: pi = pf
0 = (8m) (2v) – (16m) (v) + (48m) v’
Here v’ = absolute speed of rod
= 0
Displacement of rod = 0 Answer (d)
Question.. The point P is at
(a) The center of the rod
(b) The edge of the table supporting the end B
(c) The edge of the table supporting end A
(d) None of the above
Solution:

xA + xB = 12 L
2vt + vt = 12 L
vt = 4L
Þ XB = vt = 4L
Question. The speed of the rod after the spider eats up the moth and moves toward A is
![]() (b) v
(b) v
![]() (d) 2v
(d) 2v
Solution:
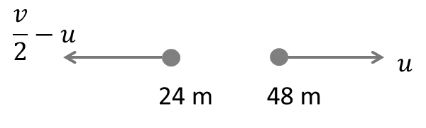
![]()
![]()
Answer (c)
Question.. After starting from end B of the rod the spider reaches the end A at a time
(a) 40 s (b) 30 s
(c) 80 s (d) 10 s
Solution: ![]()
But Lv=T=4s![]()
∴ t=80 s![]()
Answer (c)
Question. By what distance the center of mass of the rod shift during this time?
![]()
![]()
(c) L ![]()
Solution: Till t1, rod is stationary. For time t2 rod is moving with absolute speed u (= v/6)
![]()
![]() Answer (a)
Answer (a)
Linear Momentum
LINEAR MOMENTUM
![]()
Direction of Linear momentum will be just same as direction of velocity
Case I Changing of linear momentum
![]()
![]()
![]()
Note: (1) Slope of p - t graph will give us Force (F)
(2) Area under the F - t carve will gives us change in momentum
Impulse FDt =Dp Also we can say impulse is change in momentum
Example: A ball of mass 1 kg drops on the hard floor and ball strikes the floor with 10m/s rebound with same speed also. If ball remains for 0.1 sec in contact with floor. Then find
(i) Magnitude of rate of change of momentum
(ii) Rate of change of magnitude of momentum
Solution: Momentum just before strike the floor p1 = mv
p1 = - 1 x10
= - 10 kg mt/sec
Momentum just after strike the floor
p2 = + mv
= + 1 x10
= 10 kg mt/sec
(i) Magnitude of rate change of momentum
![]()
(ii) Rate of change of magnitude of momentum
Þ Magnitude of momentum is not changing only direction of momentum is changing
Þ Therefore Ans-Zero
CHANGING IN MOMENTUM
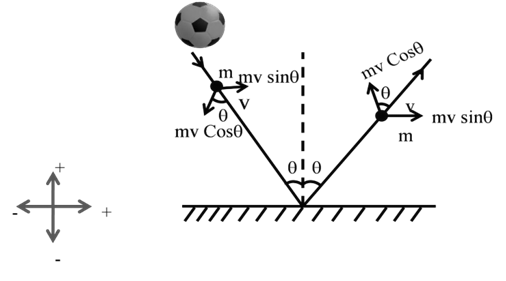
Change in momentum along x- axis Þ
p1 = mv sinq before Collision
p2 = mv sinq after Collision
(D px) = p2 – p1 = 0
Change in momentum along y-axis Þ
p1 = - mv cosq before Collision
p2 = mv cosq after Collision
(Dp)y = p2- p1 = 2 mv cosq
CHANGING IN MOMENTUM
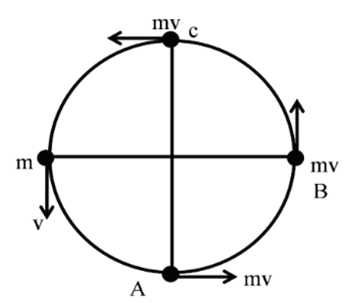
Let assume a ball attached with a string and moving uniformly in a Circular path
(i) Change in momentum from A to B
![]()
![]()
![]()
![]()
![]()
(ii) Change in momentum from A to C
![]()
![]()
![]()
i![]()
![]()
![]()
Another case
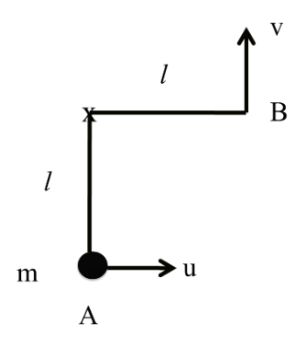
![]()
![]()
![]()
![]()
But here
v2 = u2 – 2gl
![]()
Case I Conservation of linear momentum (COLM)
![]()
![]()
![]()
![]()
![]()
Example:
Given A trolly of mass M kept at rest on a Smooth road. Two person each of mass m Standing at two ends of trolly. Now person A jumps in horizontal direction form the trolly with speed u (with respect to trolly) and then person B jumps in horizontal direction with speed u (with respect to trolly) in opposite direction. Find final speed of trolly just after both person jumps from the trolly.
Solution
Just before A jumps
p1 = (2 m + m) x 0 = 0
Just after A jumps
p2 = mu + (M + m) v1
Now Fext = 0, applying COLM
p1 = p2 Þ mu + (M + m) v1 = 0
![]()
Again if we assume that trolly and person B is at rest

Just before B jumps
p1 = (M + m) x 0 (Assume)
Just after B jumps
p2 = - mu + Mv2
Now applying COLM

p1 = p2Þ - mu + Mv2 = 0
![]()
Now Final speed of trolly after both A & B Jumps
Vf = V1 + V2
![]()
![]()
COLLISION
Head on Collision

OBLIQUE COLLISION
Types of Collisions
(1) Perfect elastic Collision.
Momentum will Conserved p1 = p2
Energy will Conserved k1 = k2
No loss of energy
Coefficient of restitution e = 1
CONCEPT OF EXCHANGE
(2) Elastic Collision
Momentum will Conserved p1 = p2
Energy will not Conserved k1¹ k2
Minimum energy loss Coefficient of restitution
e < 1 (But here e will be Close to 1)
(3) Perfect inelastic Collision
Momentum will conserved p1 = p2
Energy will not conserved k1 ≠ k2
Maximum energy loss coefficient of restitution e = 0
(4) Inelastic Collision
Momentum will Conserved p1 = p2
Energy will not Conserved k1 ¹ k2
Maximum energy loss Coefficient of restitution
e > 0 (But here e will be close to 0)
NEWTONS LAW FOR COLLISION
Speed just after Collision = e (Speed just before Collision)
Height after Collision = e2 (Height before Collision)
Total distance Covered by the ball
H = h + 2 e2 h + 2e4 h + -------
= h [ 1 + 2e2 (1 + e2 + e4 + ----)]
![]()
Variable Mass
VARIABLE MASS
![]()
Case 1
Rocket Propulsion
Thrust force on the rocket in upwards direction ![]()
Weight of rocket = mg down ward direction
![]()
![]()
![]()
![]()
![]()
![]()
If gravity (g) neglected and
u = 0 then ![]()
Case 2
Density of liquid = P Orifice area = A
![]()
![]()
![]()
![]()
![]()
![]()
![]()
A piece of wood of mass 0.03 kg is dropped from the top of a 100 m height building. At the same time, a bullet of mass 0.02 kg is fired vertically upward with velocity 100 ms-1 from the ground. The bullet gets embedded in the wood. Then, the maximum height to which the combined system reaches above the top of the building before falling below is (take, g = 10 ms-2) (2019 JEE Main, 10 Jan I)
(a) 20 m (b) 30 m
(c) 10 m (d) 40 m
Solution: Key Idea As bullet gets embedded in the block of wood so, it represents a collision which is perfectly inelastic and hence only momentum of the system is conserved.
Velocity of bullet is very high compared to velocity of wooden block so, in order to calculate time for collision, we take relative velocity nearly equal to velocity of bullet.
So, time taken for particles to collide is
![]()
Speed of block just before collision is
v1 = gt = 10 x 1 = 10 ms-1
Speed of bullet just before collisions is
v2 = u – gt
= 100-10 x 1 = 90 ms-1
Let v = velocity of bullet + block system, then by conservation of linear momentum, we get
- (0.03 x 10) + (0.02 x 90) = (0.05)v
Þ v = 30 ms-1
Now, maximum height reached by bullet and block is
![]()
Þ h = 45 m
Height covered by the system from point of collision = 45 m
Now, distance covered by bullet before collision in 1 sec.
![]()
Distance of point of collision from the top of the building = 100 – 95 = 5m
Maximum height to which the combined system reaches above the top of the building before falling below = 45 – 5 = 40 m
Answer (d)
Question. n elastic balls are placed at rest on a smooth horizontal plane which is circular at the ends with radius r as shown in the figure. The masses of the ball are![]() respectively. What is the minimum velocity which should be imparted to the first ball of mass m such that nth ball completes the vertical circle
respectively. What is the minimum velocity which should be imparted to the first ball of mass m such that nth ball completes the vertical circle
![]()
![]()
![]()
![]()
Solution: Velocity of second ball
![]()
![]()
Day – 5 and 6 Question Practice Online
Velocity of third ball will become,
![]()
![]()
![]() Answer (a)
Answer (a)
Equilibrium
(1) STABLE EQUILIBRIUM

![]()
![]()
![]()
![]()
(2) UNSTABLE EQUILIBRIUM

![]()
![]()
![]()
(3) NEUTRAL EQUILIBRIUM
![]()
![]()
Question: The given plot shows the variation of U, the potential energy of interaction between two particles with the distance separating them r.
1. B and D are equilibrium points
2. C is a point of stable equilibrium
3. The force of interaction between the two particles is attractive between points C and D and repulsive between D and E
4. The forces of interaction between particles is repulsive between
points E and F.
Which of the above statements are correct?
(a) 1 and 2 (b) 1 and 4
(c) 2 and 4 (d) 2 and 3
Solution: At C, potential energy is minimum. So, it is stable equilibrium position.

Further,
![]()
Negative force means attraction and positive force means repulsion.
Question: The potential energy f in joule of particle of mass 1 kg moving in x-y plane obeys the law, f = 3x + 4y. Here, x and y are in metres. If the particle is at rest at (6m, 8m) at time 0, then the work done by conservations force on the particle from the initial position to the instant when it crosses the x-axis is
(a) 25 J (b) -25 J
(c) 50 J (d) -50 J
Solution:j![]()
![]()
Since, particle was initially at rest. So, it will move in the direction of force.
We can see that initial velocity is in the direction of PO. So the particle will cross the X-axis at origin.
Ki + Ui = Kf + Uf
0 + ( 3 x 6 + 4 x 8) = Kf + (3 x 0+ 4 x 0)
or Kf = 50 J Answer (c)
Gravitational potential
GRAVITATIONAL POTENTIAL
Work done per unit mass in shifting a rest mass from some reference point (usually at infinity) to the given point.
![]()
![]()
Potential Energy: it is the energy stored in a body or system by virtue of its configuration or its position in a fields.
F= -dUdr⇒F.dr= -dU![]()
POTENTIAL DUE TO POINT MASS
Suppose a point mass ‘M’ placed at origin (x = 0). We wish to find gravitational potential at P, at a distance ‘r’ from M.
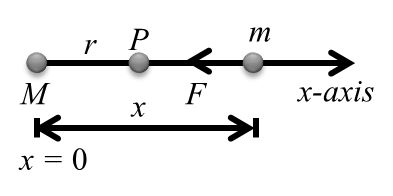
First of all we will calculate the work done by gravitational force in moving a test mass ‘m’ from infinity to P. Gravitational force on ‘m’ when it is at a distance ’x’ from M is
![]() Here, negative sign implies that forces is towards ‘M’ or towards negative x-direction. This is a variable force (a function of x). Therefore, work done is
Here, negative sign implies that forces is towards ‘M’ or towards negative x-direction. This is a variable force (a function of x). Therefore, work done is
![]()
Now, from the definition of potential,
![]()
![]()
Potential due to a Uniform Solid Sphere
Potential at some External Point
The gravitational potential due to a uniform sphere at an external point is same as that due to a single particle of same mass placed at its centre. Thus,
![]()
At the surface, ![]()
Potential at some Internal Point
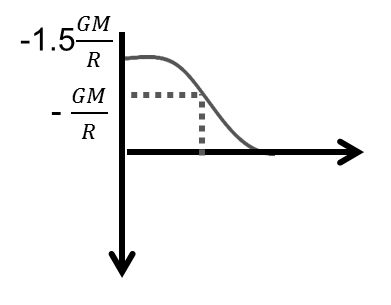
At some internal point, potential at a distance r from the centre is given by,
![]()
![]()
![]()
i.e. at the centre of the sphere the potential is 1.5 times
the potential at the surface. The variation of V versus r
graph is as shown in Fig.
Potential due to a Uniform Thin Spherical Shell
Potential at an External Point
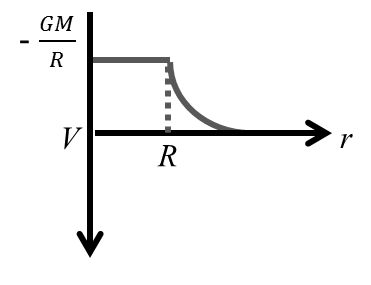
To calculate the potential at an external point, a uniform spherical shell may be treated as a point mass of same magnitude at its centre. Thus, potential at a distance r is given by,
![]()
![]()
Potential at an Internal Point
The potential due to a uniform spherical shell is constant at any
point inside the shell and this is equal .![]() Thus, V-r
Thus, V-r
graph for a spherical shell is as shown in Fig.
Potential due to a Uniform Ring at some Point on its Axis
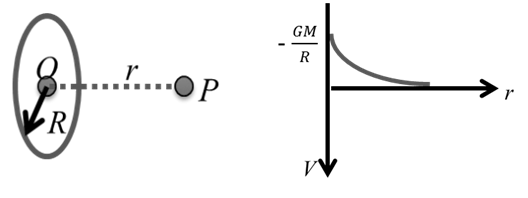
The gravitational potential at a distance r from the centre on the axis of a ring of mass M and radius R is given by,
![]()
![]()
![]()
The V-r graph is as shown in Fig.
Difference in Potential Energy (D U)
Let us find the difference in potential energy in two positions shown in figure. The potential energy when the mass is on the surface of earth (at B) is,
![]()
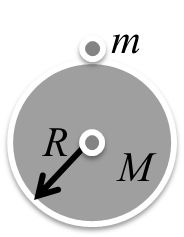
and potential energy when the mass m is at height h above the surface of earth (at A) is,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
For h < < R, DU » mgh
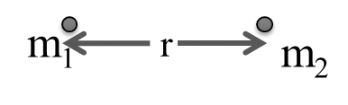
Thus , mgh is the difference in potential energy (not the absolute energy), for h < < R.
![]()
Note: For attraction force U → negative
For repulsion force U → Positive
POTENTIAL ENERGY FOR SYSTEM OF PARTICLES
![]()
Potential energy on the surface of earth
U = - mgR (But we can assume is zero)
Potential energy at h height above the earth surface
![]()
If h <<<<<<R
U = mgh
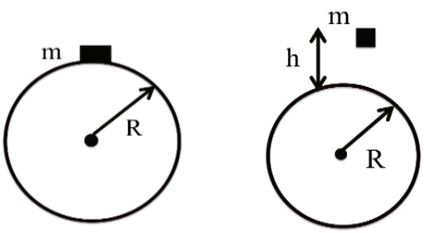
ORBITAL VELOCITY
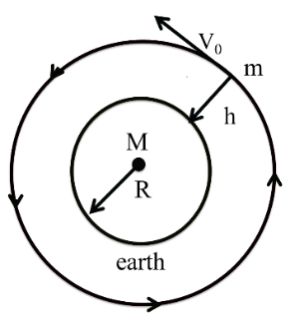
![]()
![]()
![]()
![]()
![]()
![]()
Time period
![]()
![]()
![]()
![]()
![]()
KINETIC ENERGY
![]()
If R + h = r
![]()
POTENTIAL ENERGY
![]()
Total Energy E = K + U
![]()
![]()
Escape velocity
Potential energy at the surface of earth
![]()
![]()
![]()
![]()
![]()
![]()
Ve = 11.3 km/sec
Independent of mass
Angular momentum
ANGULAR MOMENTUM
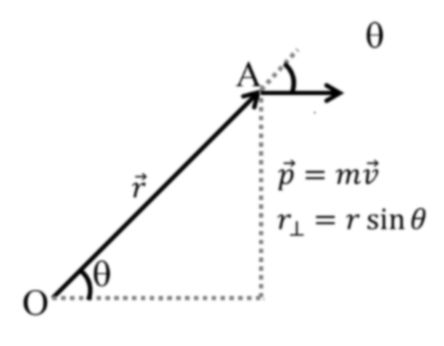
(ii) Angular Momentum of a Rigid Body Rotation about a Fixed Axis

Uniform Pure Rolling

vp = vQ
v - Rw = 0
v = Rw
If vp > vQ or v > Rw, the motion is said to be forward slipping and if vp < vQ or v < Rw, the motion is said the backward slipping
Accelerated Pure Rolling
v = Rw
![]()
at = Ra
![]()
![]()
![]()
![]()
Rolling on Rough Incline plane
![]()
![]()
![]()
![]()
![]()
Isolid < Ihollow or asolid > ahollow
tsolid < thollow
![]()
Case
A block of mass m and a cylinder of mass 2m are released on a rough inclined plane, inclined at an angle ![]() with the horizontal. The coefficient of friction for all the contact surface is 0.5 find the accelerations of the block and the cylinder.
with the horizontal. The coefficient of friction for all the contact surface is 0.5 find the accelerations of the block and the cylinder.
Assume pure rolling.
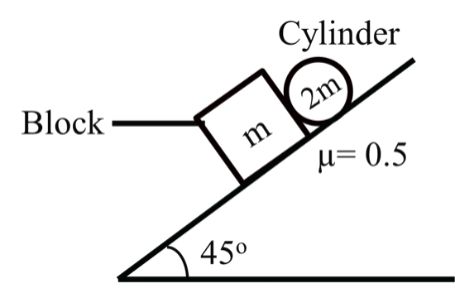
If the block and cylinder move independently on the incline, their acceleration are
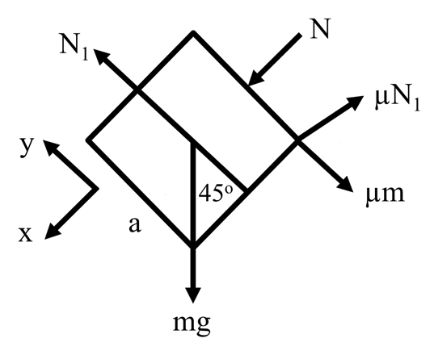
![]()
![]()
![]()
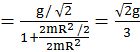
![]() So, both the bodies will move in contact
So, both the bodies will move in contact
with each other with common acceleration a which we have to calculate.
Free body diagram of block is as shown.
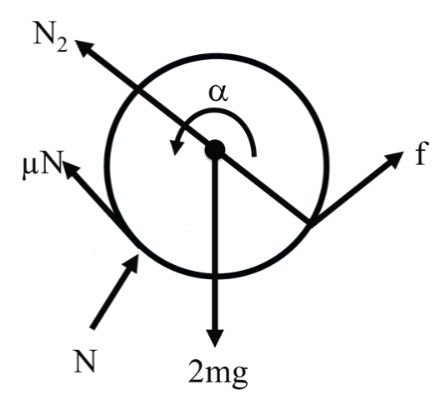
![]()
![]() …..(i)
…..(i)
![]()
![]() ….(ii)
….(ii)
From Eqs. (i) and (ii), we get
![]()
The free body diagram of cylinder is as shown.
![]()
![]()
And ![]()
![]()
From Eqs. (iv) and (v), we get
![]()
Using this in Eq. (iii), we get ![]()
Case:- Ladder → mass = m, Length = L
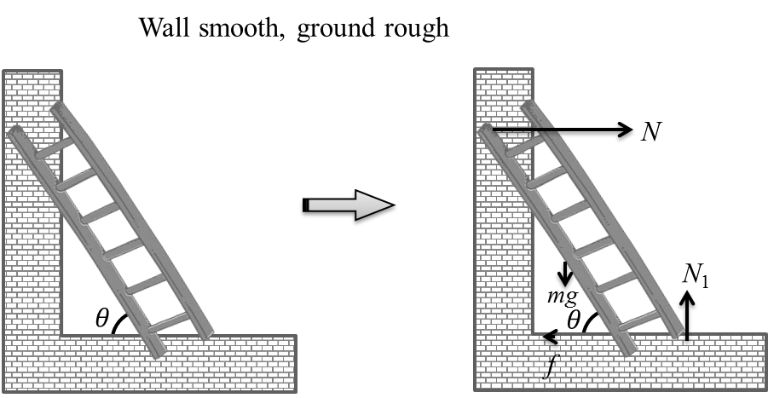
For equilibrium
f – N = 0
N1 – mg = 0
Torque about C. M. of Ladder
![]()
Substitute value of N1 and f
![]()
![]()
Case:- Topping and Sliding
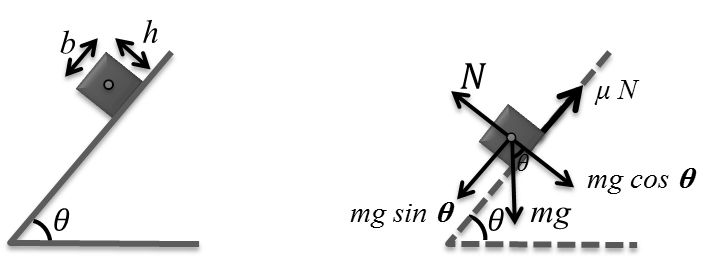
For translational equilibrium
![]()
![]()
For rotational equilibrium
![]()
![]()
![]()
![]() block has a tendency to slide before topple
block has a tendency to slide before topple
![]() block has a tendency to topple before slide
block has a tendency to topple before slide
![]() block slides down
block slides down
![]() block topples
block topples
Straight line motion, Fixed axis rotation
Kinetic Energy of a Rigid Body Rotating About a Fixed Axis

![]()
![]()
![]()
![]()
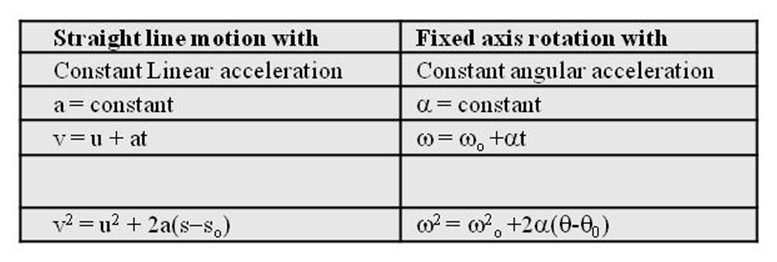
A uniform flat disc of mass M and radius R rotates about a horizontal axis through its center with angular speed ![]()

What is its angular momentum?
![]()
![]()
![]()
![]()
![]()
A chip of mass m breaks of the disc at an instant such that the chip rises vertically above the point at which it breaks off. What is the maximum height the chip rises to from the location of its breaking? (no impulses internal force acts on the chip)
![]()
![]()
![]()
![]()
In the process, the mechanical energy of the chip remains constant.
![]()
What are the final angular momentum and energy of the disc?
![]()
![]()
![]()
![]()
![]()
![]()
EXTRA POINTS TO REMEMBER
In case of pure rolling on a stationary horizontal ground (when v = Rw), following points are important to note:
Distance moved by the center of mass of the rigid body in one full rotation is 2pR.
This is because ![]()
In forward slipping s > 2pR
And in backward slipping s > 2pR
The speed of a point on the circumference of the body at the instant shown in figure is .![]()
![]()

This can be shown as:
![]()
From the above expression we can see that:
![]()
![]()
![]()
The path of a point on circumference is a cycloid and the distance moved by this point in one full rotation is 8R.
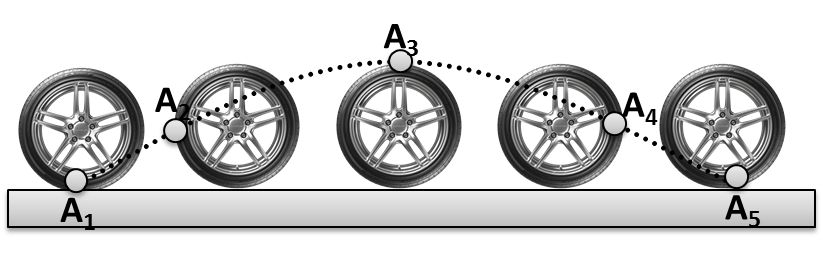
In the figure, the dotted line is a cycloid and the distance A1A2…..A5 is 8R. this can be proved ![]()
Speed of point A at this moment is, ![]()
Distance moved by it is in time dt is, ![]()
Therefore, total distance moved in one full rotation is,
![]()
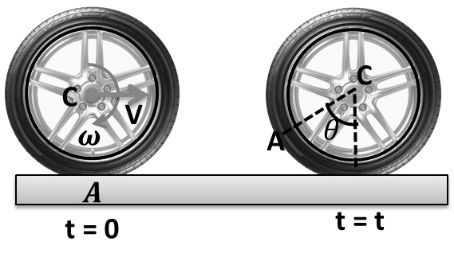
On integration we get, s = 8R.
![]()
![]()
![]()
![]()
Here, KR stands for rotational kinetic energy ![]() for translation kinetic energy
for translation kinetic energy ![]()
For example, for a disc
![]()
![]()
![]()
Case 3
A frame of the reference that is accelerated with respect to an inertial frame of reference is called a non –inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity w is an example of a non –inertial frame of reference. The relationship between the force Frot experienced by a particle of mass m moving on the rotating disc and the force Fin experienced by a particle of mass m moving on the rotating disc and the force Fin experienced by the particle in an inertial frame of reference is, ![]() , where, vrot is the velocity in the rotating frame of reference and r is the position vector of the particle with respect to the center of the disc.
, where, vrot is the velocity in the rotating frame of reference and r is the position vector of the particle with respect to the center of the disc.
Now, consider a smooth slot along a diameter of a disc of radius R rotating counter –clockwise with a constant angular speed w about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the X –axis along the slot, the Y –axis perpendicular to the slot and the z –axis along the rotation axis (w = wk). A small block of mass m is gently placed in the slot at![]() and is constrained to move only along the slot.
and is constrained to move only along the slot.
Force on block slot![]()
![]()
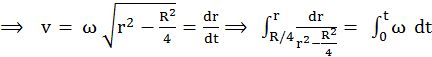
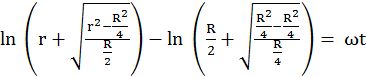
![]()
![]()
![]()
The net reaction of the disc on the block is
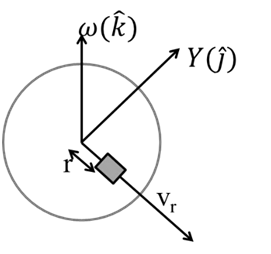
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Also, reaction is due to disc surface then
![]()
Case 4
A thin uniform bar lies on a frictionless horizontal surface and is free to move in any way on the surface. Its mass is 0.16 kg and length is ![]() m. Two particles, each of mass 0.08 kg are moving on the same surface and towards the bar, one with a velocity 10 ms-1 and the other with 6 ms-1 as shown in the figure. The first particle strikers the bar at point A and the other at point B. Each of A and B is at a distance of 0.5 m from the center of the bar. The particle strike the bar at the same instant of time and stick to the bar after collision.
m. Two particles, each of mass 0.08 kg are moving on the same surface and towards the bar, one with a velocity 10 ms-1 and the other with 6 ms-1 as shown in the figure. The first particle strikers the bar at point A and the other at point B. Each of A and B is at a distance of 0.5 m from the center of the bar. The particle strike the bar at the same instant of time and stick to the bar after collision.
The velocity of center of mass of the system just after impact (in ms-1) is
(a) 1 (b) 2 (c) 3 (d) 4
Let v be the center of mass is at rest all the times, because of conversation of linear momentum. So, linear velocity of the system must be zero.
From law of conversation of linear momentum.
![]()
V = 4 ms-1
The angular velocity of the system just after impact (in rad/s) is
(a) 8 (b) 4 (c) 2 (d) 1
AC = BC = 0.5 m
From conversation of angular momentum about C
(0.08)(10)(0.5)-(0.08)(6) (0.5) ![]()
Where, ![]()
![]()
![]()
Using this in the equation above, we get ω![]()
Case 5
A light ring with three rods, each of mass m is welded on this ring. The rods form an equilateral triangle. The rigid assembly is released on a rough fixed inclined plane. Determine the minimum value of the coefficient of static friction that will allow pure rolling of the assembly.
![]()
![]()
![]()
![]()
![]()
![]() ….(i)
….(i)
![]()
![]() ……(ii)
……(ii)
![]() ….(iii)
….(iii)
For no slipping ![]() …..(iv)
…..(iv)
The moment of inertia of the assembly about its center of mass is
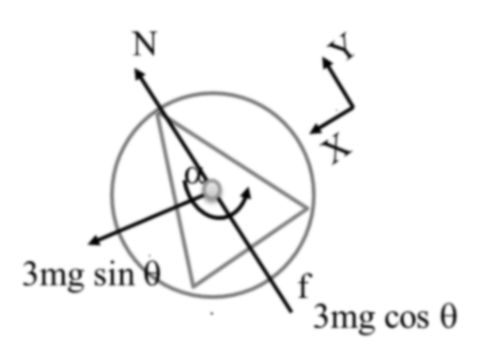
![]()
Now, on solving Eqs. (i), (ii), (iii) and (iv) simultaneously, we obtain
![]()
If µ is the coefficient of fricti on at the contact surface, then
![]()
![]()
![]()
![]()
![]()

 Kaysons Publication
Kaysons Publication
