Gravitational potential

GRAVITATIONAL POTENTIAL

Work done per unit mass in shifting a rest mass from some reference point (usually at infinity) to the given point.

 

 

Potential Energy: it is the energy stored in a body or system by virtue of its configuration or its position in a fields.

F= -dUdr⇒F.dr= -dU  

 

POTENTIAL DUE TO POINT MASS

Suppose a point mass ‘M’ placed at origin (x = 0). We wish to find gravitational potential at P, at a distance ‘r’ from M.

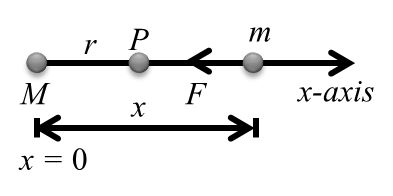
First of all we will calculate the work done by gravitational force in moving a test mass ‘m’ from infinity to P. Gravitational force on ‘m’ when it is at a distance ’x’ from M is 

 Here, negative sign implies that forces is towards ‘M’ or towards negative x-direction. This is a variable force (a function of x). Therefore, work done is

 

Now, from the definition of potential,

 

 

Potential due to a Uniform Solid Sphere

Potential at some External Point

The gravitational potential due to a uniform sphere at an external point is same as that due to a single particle of same mass placed at its centre. Thus,

 

At the surface,                         

Potential at some Internal Point

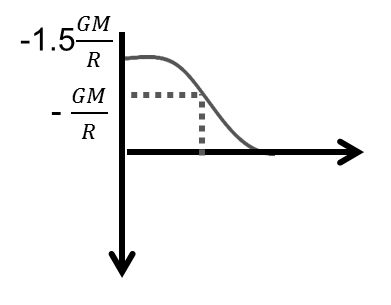
At some internal point, potential at a distance r from the centre is given by,

 

 

 

i.e. at the centre of the sphere the potential is 1.5 times

the potential at the surface. The variation of V versus r

graph is as shown in Fig.

Potential due to a Uniform Thin Spherical Shell

Potential at an External Point

To calculate the potential at an external point, a uniform spherical shell may be treated as a point mass of same magnitude at its centre. Thus, potential at a distance r is given by,

 

 

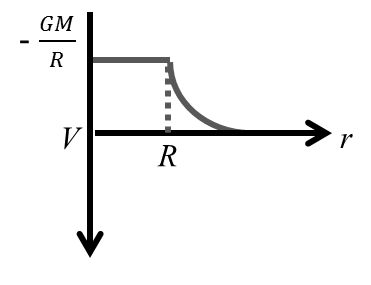
Potential at an Internal Point

The potential due to a uniform spherical shell is constant at any

point inside the shell and this is equal .  Thus, V-r

graph for a spherical shell is as shown in Fig.

Potential due to a Uniform Ring at some Point on its Axis

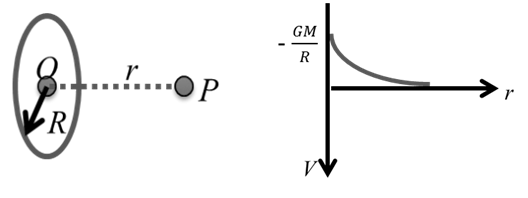
The gravitational potential at a distance r from the centre on the axis of a ring of mass M and radius R is given by,

 

 

 

The V-r graph is as shown in Fig.

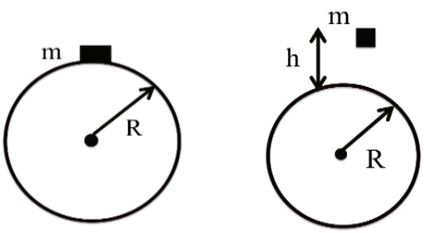
Difference in Potential Energy (D U)

Let us find the difference in potential energy in two positions shown in figure. The potential energy when the mass is on the surface of earth (at B) is,

 

and potential energy when the mass m is at height h above the surface of earth (at A) is,

 

 

 

 

 

 

For      h < < R, DU » mgh

Thus , mgh is the difference in potential energy (not the absolute energy), for h < < R.

 

Note: For attraction force U → negative

For repulsion force U → Positive

POTENTIAL ENERGY FOR SYSTEM OF PARTICLES

Potential energy on the surface of earth

U = - mgR (But we can assume is zero)

Potential energy at h height above the earth surface

 

If h <<<<<<R

U = mgh

ORBITAL VELOCITY

 

 

 

 

 

 

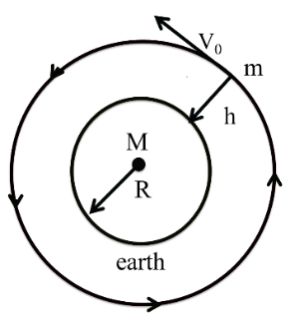
Time period

 

 

 

 

KINETIC ENERGY

 

 

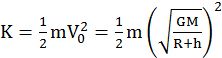
If R + h = r

 

POTENTIAL ENERGY

 

Total Energy E = K + U

 

 

Escape velocity

Potential energy at the surface of earth

 

 

 

 

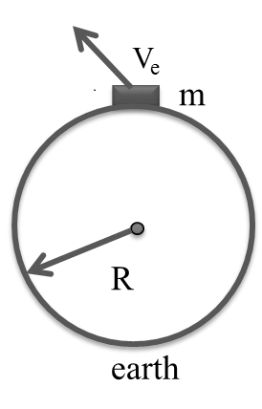
V_e = 11.3 km/sec

Independent of mass