Force, Constraint equation

Force:- Any pull or push”,     unit: kg met/sec² or Newton (N)

Types of forces:-
1- Field Forces:- No need of contact

Always attraction type

 

Direction:- Always along (-y) axis or straight vertically down ward.

(2). Contact forces: There must be some contact

(i) Normal force (N):- This force act when two surfaces of different object are in contact.

Direction:- perpendicular to contact surfaces.

(ii). Frictional force(f):- This force also act when two surfaces of different objects in contacts.

Direction:- Parallel to contact surfaces

Also F = m N here m is coefficient of friction.

Now

N → Perpendicular to contact surface

So F ^ N  

 

Understanding of frictional force

The force which resist the motion”

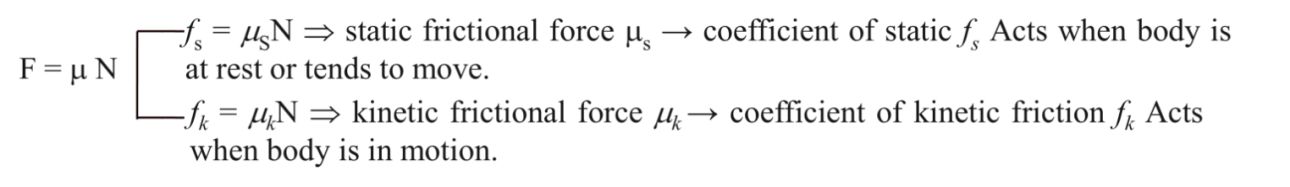
m_S > m_k      m can be less than or greater than one

If F_ext = 0, f = 0

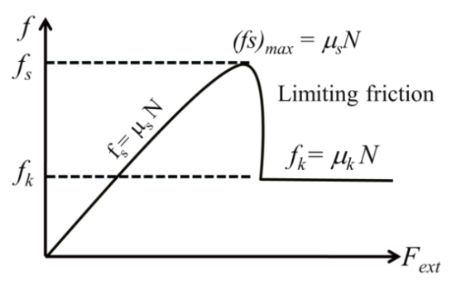
Example:- 1

Now

f_s = m_sN

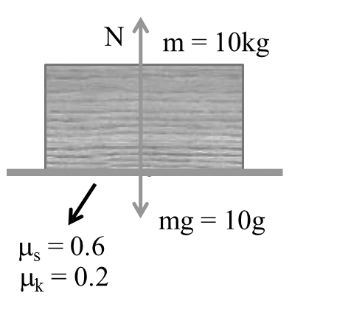
 = m_s mg

 = 0.6 x 10 x 10

f_s = 60 N

f_k = m_kN

 = 0.2 x 10 x10

f_k = 20 N

Amount of frictional force = 0

Because f_ext = 0, = f = 0

 

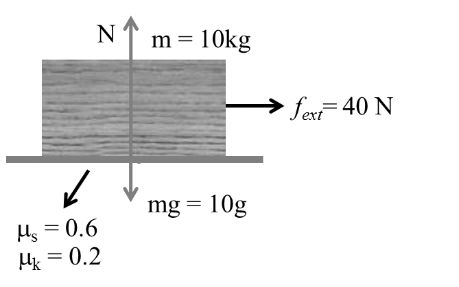
Example:- 2

m = 10 kg As in case (i)  f_s = 60 N, f_k = 20 N

f = f_s = 40 N

Body is at rest

 

Example:- 3

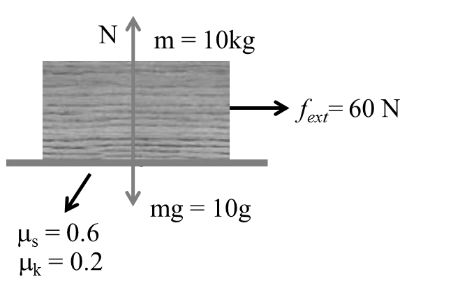
As in case (i) f_s = 60N, f_k = 20 N

f = f_s = 60 = F_ext →    limitation friction

Body is at rest but tends to move

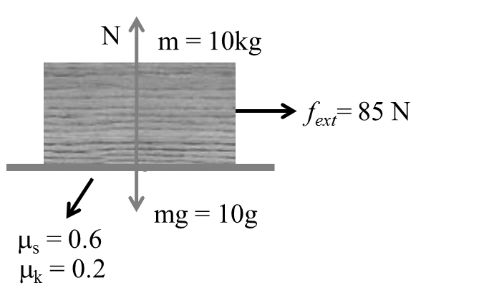
Example:- 4

As in case = f_s = 60N, f_k = 20N

Body is  in moving condition

10a = 85 - 20

f = f_k = 20 N

(3) Attachment forces indirect force

 

Direction: Direction of tension (T) is always away from the body. 

Example:-                                  

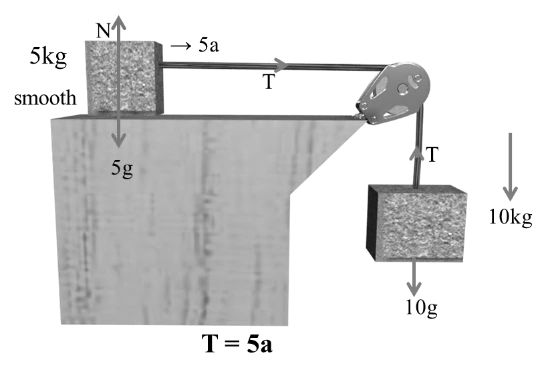
10 g –T = 10 a   ---- (1)

N = 5 g      ------(2)

T = 5a --------(3)

Solving 1& 310 g - 5a = 10a

15a = 10g

            

 

T = 5a

                 

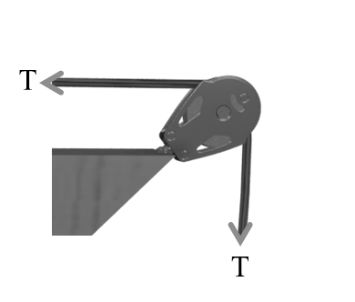
Net force on the pulley

Example:-

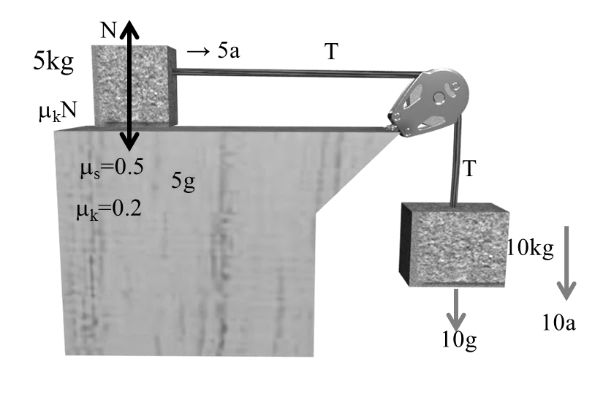
f_s = m_s N

   = 0.5 x 5g

f_s = 25 N

f_k = m_k N

    = 0.2 x 5g

f_k = 10 N

Pulling force for  5 kg

10 g = 100 N

So both block will move

10 g –T = 10a -----(1)

T -m_kN = 5a ------(2)

T – 10 = 5a

N = 5g -----(3)

Solving  (1) & (2)

10g –T = 10a

1-10 = 5a

90 = 15a Þ2

Similarly

T -10 = 5 x 6                        T= 40N