CONCEPTS BASED ON LOCATION OF CM
Concept (1) Addition of masses
Given a small disc of radius R, thickness t is put over a large disc of same material and thickness, radius 2R- Finding C.M. of Combined System of two disc.
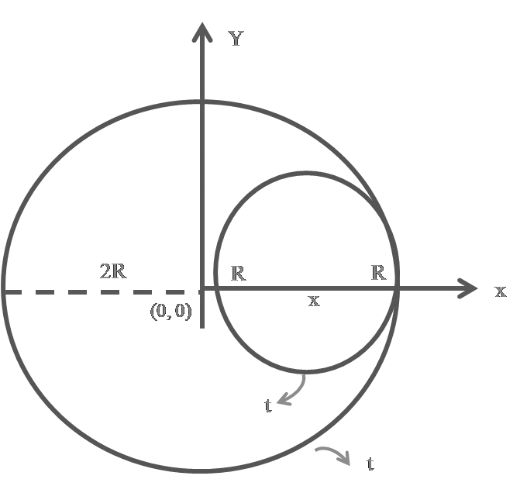
Step:- Fixed your Origin
![]()
![]()
Here ![]() is density and t is thickness so m α A
is density and t is thickness so m α A
![]()
Area of small disc = p(R)2 = pR2
![]()
![]()
![]()
Concept 2. Cutting of masses (Cavity)
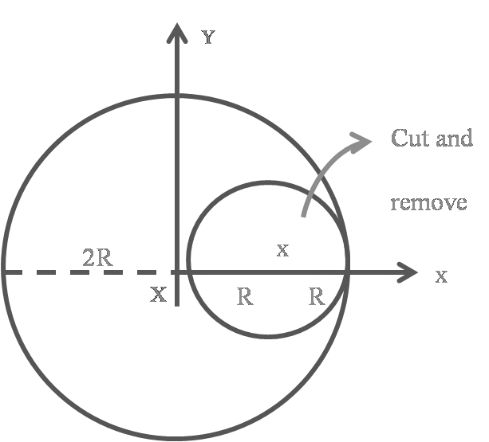
In this case a small disc of radius R is cutting from a large disc of radius 2R. Now finding C.M. of remaining part of the disc
![]()
![]()
![]() So CM is located at left side form origin at distance R/3
So CM is located at left side form origin at distance R/3
Concep.3 Motion of CM
![]()
![]()
![]()
![]()
![]()
Concept 4. Shifting of C. M.
![]()
![]()
![]()
Example

Given if 2 kg block displace by 4 meter due right and 8 kg block displace by 2 meter due left then changing in position of C.M.
![]()
![]()
So C.M. will shift by 0.2 meter due left side
Example:
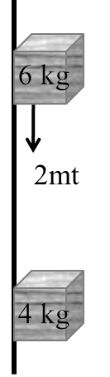
If 6 kg block moves towards down ward by 2 meter and if CM is to be Shift by +3 met in upward direction then amount and direction to which we have to shift 4 kg block.
D Ycm = + 3 mt
![]()
![]()
30 = - 12 + 4 DY2
Concept: 5 If Fext = 0 then C.M. will not move
Example: Given a boat of mass 50 kg is stationary on a lake. Two Person A and B are initially at two ends of the boat. Now both start to move towards each other and reach the center of the boat. So what will be the distance and direction boat will move.

Solution
![]()
![]()
![]()
![]()
(xcm)f = 7.5 mt,
Boat displace
(xcm)f – (xcm)i
= 7.5 - 6.5
= 1 met
Boat will move due left by 1 meter
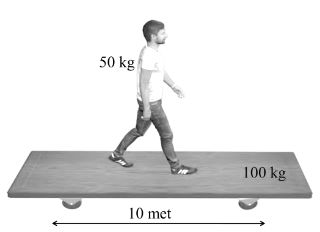
Example: A trolley of mass 100 kg, length 10 mt along with a person of mass 50 kg is initially at rest. But now person moves towards other end of the trolley and reach to other end of the trolley. During this process distance with respect to ground moved by person and trolley. Here we are assuming that trolley is on the smooth surface.

Solution
![]()
![]()
![]()
![]()
Trolly will move by (xcm)f – (xcm)i
6.6 – 3.3
≈ 3.3 met due left side
CONCEPT .6 ACCELERATION OF CM
Example
Finding acm = ?
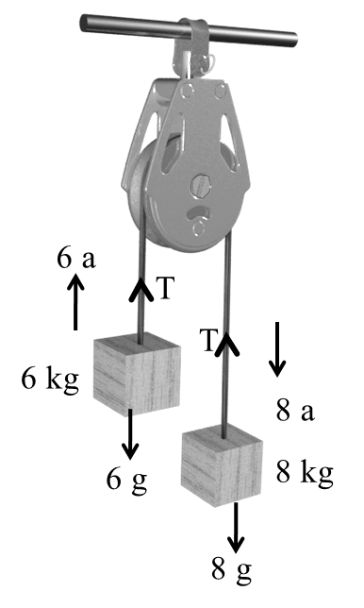
8g - T = 8a
T - 6g = 6 a
2g = 14 a
![]()
![]()
![]()
= -![]()
![]()
acm = - 0.2 m/s2
![]()
![]()
![]()
A uniform bar of length 12 L and mass 48 m is supported horizontally on two fixed smooth tables as shown in figure. A small moth (an insect) of mass 8m is sitting on end A of the rod and a spider (an insect) of mass 16 m is sitting on the other end. B. Both the insects moving towards each other along the rod with moving at speed 2v and then spider at half this speed (absolute). They met at appoint P on the rod and the spider eats the moth. After this the spider moves with a velocity ![]() relative the end A. The spider takes negligible time in eating on the other . Also, let
relative the end A. The spider takes negligible time in eating on the other . Also, let ![]() where T is a having value 4s.
where T is a having value 4s.
Question. Displacement of the rod by the time the insect meet the moth is
![]() (b) L
(b) L
![]() (d) zero
(d) zero
Solution: pi = pf
0 = (8m) (2v) – (16m) (v) + (48m) v’
Here v’ = absolute speed of rod
= 0
Displacement of rod = 0 Answer (d)
Question.. The point P is at
(a) The center of the rod
(b) The edge of the table supporting the end B
(c) The edge of the table supporting end A
(d) None of the above
Solution:

xA + xB = 12 L
2vt + vt = 12 L
vt = 4L
Þ XB = vt = 4L
Question. The speed of the rod after the spider eats up the moth and moves toward A is
![]() (b) v
(b) v
![]() (d) 2v
(d) 2v
Solution:
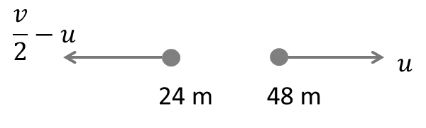
![]()
![]()
Answer (c)
Question.. After starting from end B of the rod the spider reaches the end A at a time
(a) 40 s (b) 30 s
(c) 80 s (d) 10 s
Solution: ![]()
But Lv=T=4s![]()
∴ t=80 s![]()
Answer (c)
Question. By what distance the center of mass of the rod shift during this time?
![]()
![]()
(c) L ![]()
Solution: Till t1, rod is stationary. For time t2 rod is moving with absolute speed u (= v/6)
![]()
![]() Answer (a)
Answer (a)

 Kaysons Publication
Kaysons Publication
