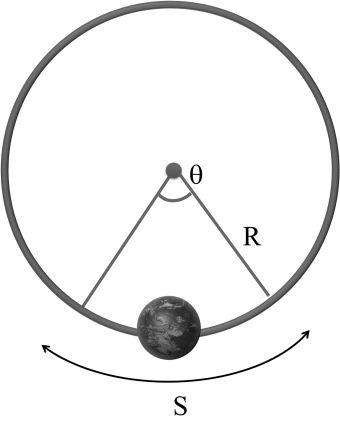
If Any object moves such that it covers an angle q at the fixed point (center of the circle) and its gap from the fixed point remains constant (radius of the circle)
![]()
![]()
Here R is constants
![]()
![]()
Now finding linear speed of
(i) hour hand (30 cm)
(ii) Minute hand (90 cm)
(iii) Second hand (60 cm)
Solution:- (i) time period of hour hand T = 12 hr

= 12 x 3600 sec
v = r w
![]()
(ii) Minute hand:- time period = T = 60 min = 60 x 60 sec
![]()
(iii) Second hand:-
Time period= T = 60 sec
v = r w
![]()
Types of circular motion: (on the basis of speed)
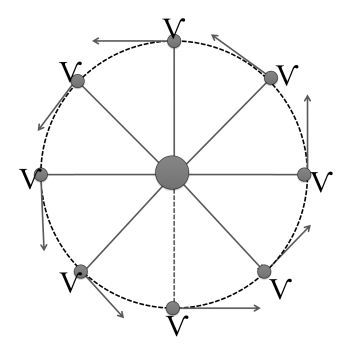
(1) Uniform circular motion: (U C M)
Only direction of velocity is changing, magnitude remains unchanged.
![]()
Now acceleration due to change in direction of velocity
![]()
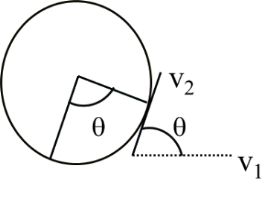
Using law of parallelogram
![]()
![]()
![]()
= 2v2 - 2v2 cosq
= 2v2 (1- cosq)
![]()
![]()
![]()
Now
![]()
![]()
sinq » q if q <<<<
![]()
![]()
a = v w,
![]()
![]()
![]()
Direction of this acceleration is towards center
![]()
Centripetal acceleration or Radial acceleration
(2) Non uniform circular motion (Non U C M)
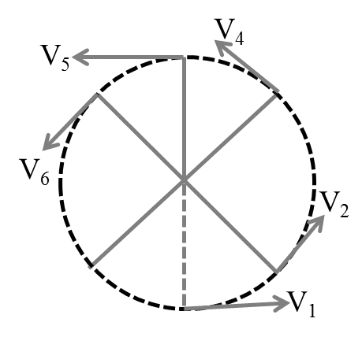
Here in this case direction as well as magnitude both are changing continuously therefore here two different named acceleration will be as,
(i) ac = aR (centripetal or radial acceleration)
(ii) at (Tangential acceleration)
Now,
Tangential acceleration.
“Rate of change of magnitude of velocity”
v = R w
![]()
![]()
![]()
So at ^ ac
![]()
Net acceleration for non-uniform circular motion.
Example:- A particle moving in a circular path of radius 2 meter and its velocity varies as v = 10t2. Then net acceleration of the particle at t = 2 sec.
Solution: Given v = 10t2
![]()
= 20 x 2
= 40 m/s2
![]()
![]()
Centripetal force:- the force require to move in a circular path for any object with respect to inertial frame is called centripetal force.
![]()
Note:- Centrifugal force will also have same magnitude but direction opposite to centripetal force.
Direction of this force is towards the center.
HORIZONTAL CIRCULAR MOTION

(1) Only banking
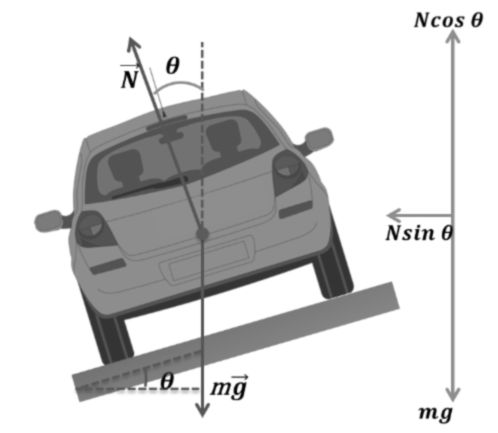
Here N sinq is C.P. provider
![]()
But N cosq = mg
![]()
![]()
Safe speed
(2) Only friction
Here now m N is C.P. provider

![]()
N = mg
![]()
![]()
![]()
Safe speed
Friction and Banking both:- To prevent inward sliding
cosq + m N sinq = mg
![]()
Divide
![]()
![]()

TO PREVENT OUTWARD SLIDING
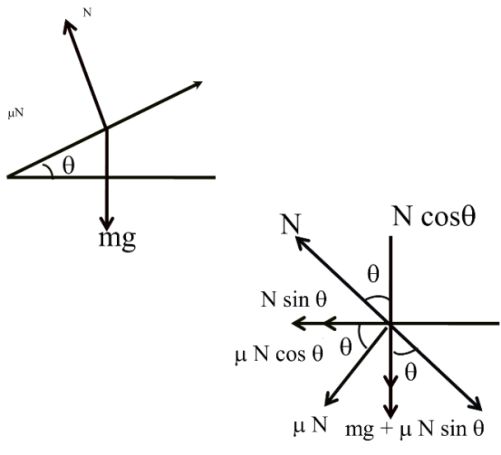
![]()
N cosq - m N sinq = mg
![]()
![]()
v1 < Vsafe < v2
![]()
CONICAL PENDULUM
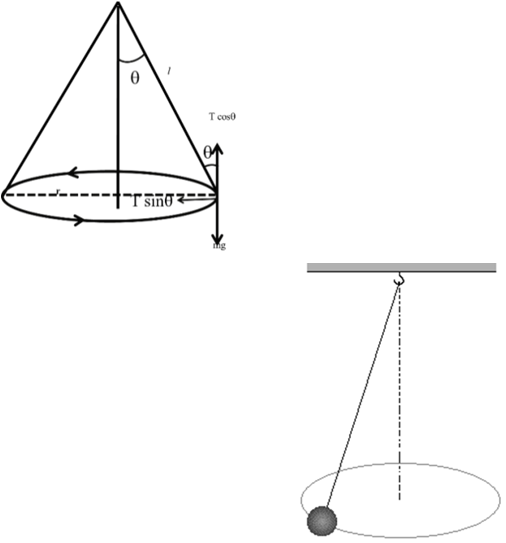
T sinq = mrw2
T cosq = mg
![]()
![]()
![]()
Time period of conical pendulum
![]()
![]()
![]()
![]()

 Kaysons Publication
Kaysons Publication
