Center of Mass and Momentum Notes for JEE Physics : EduMple

Centre of mass

It is a point of a body or system at which the whole mass of body or system is supposed to be Concentrated for dealing its translation motion.

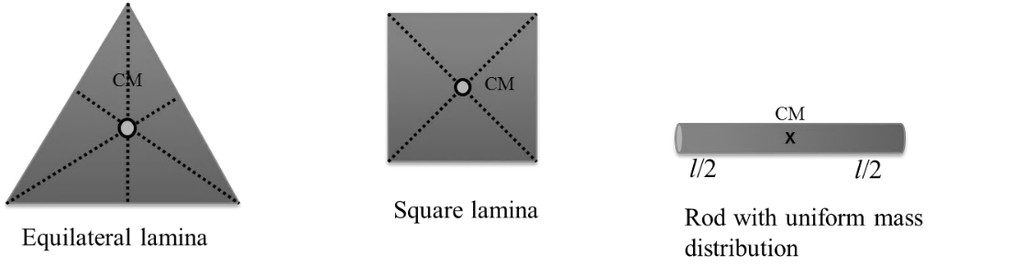
Properties of center of mass

(1) Three may or may not be any mass present physically at center of mass. So its position depends on shape of the body.

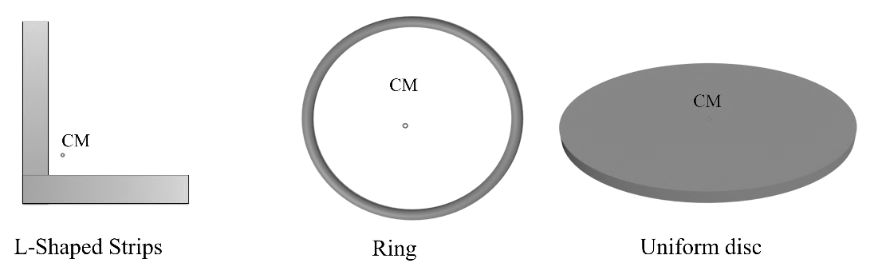
(2) For a given shape it depends on the distribution of mass within the body and is closer to massive part.

(3) If we apply the external force on cm then we will get maximum results

TO LOCATE CENTRE OF MASS

x- Coordinate of CM

y-Co-ordinate of CM

z-Co- ordinate of CM

Similarly in terms of position Vector

Example

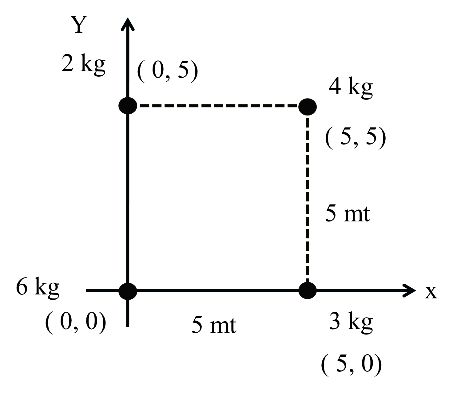
Step1. Choose your origin (try to fix your origin at extreme left and lower end)

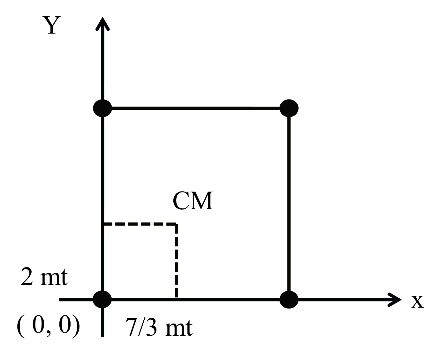
Step 2. Use above results e.g. x_cm, y_cm etc.

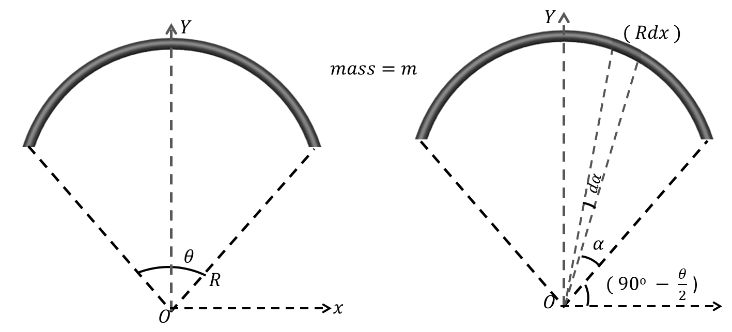
POSITION OF CENTRE OF MASS Arc of thin ring

0

PART OF THE DISC

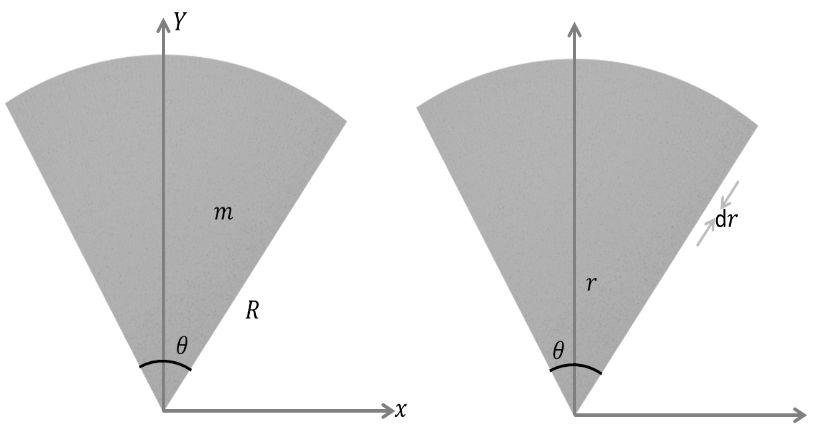
LOCATION OF C.M OF SOME HOMOGENEOUS RIGID BODIES

(1) Semi Circular ring

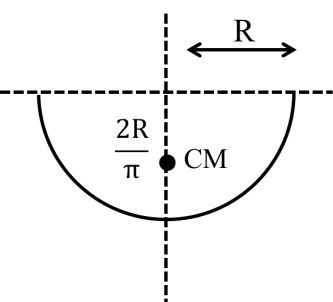
(2) Semi Circular disc

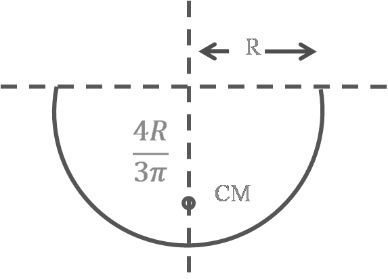
(3) Hollow hemisphere

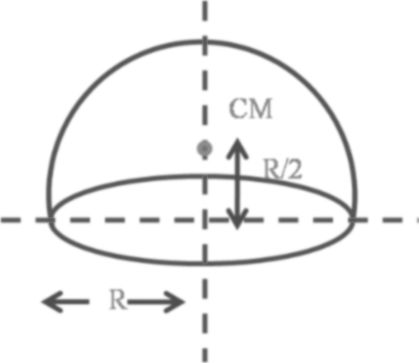
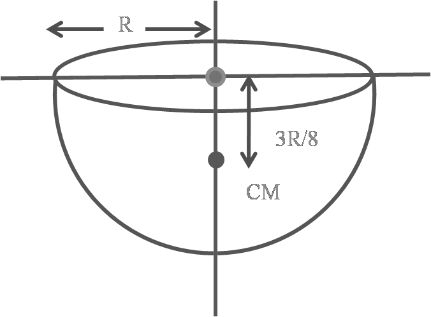
(4) Solid hemisphere

(5) Cone (Hollow)

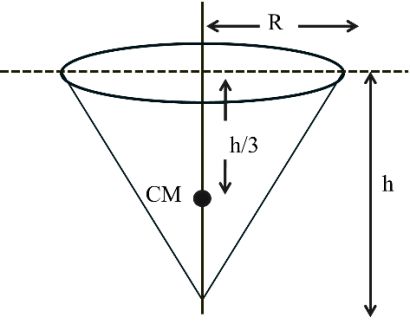
(6) Solid cone

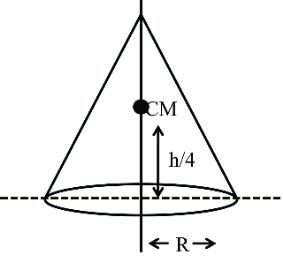
CONCEPTS BASED ON LOCATION OF CM

Concept (1) Addition of masses

Given a small disc of radius R, thickness t is put over a large disc of same material and thickness, radius 2R- Finding C.M. of Combined System of two disc.

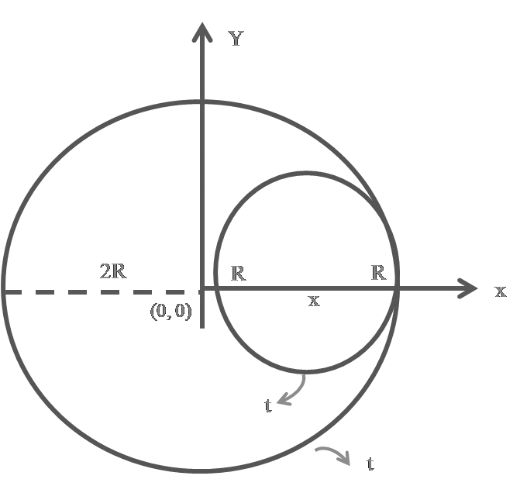
Step:- Fixed your Origin

Here is density and t is thickness so m α A

Area of small disc = p(R)² = pR²

Concept 2. Cutting of masses (Cavity)

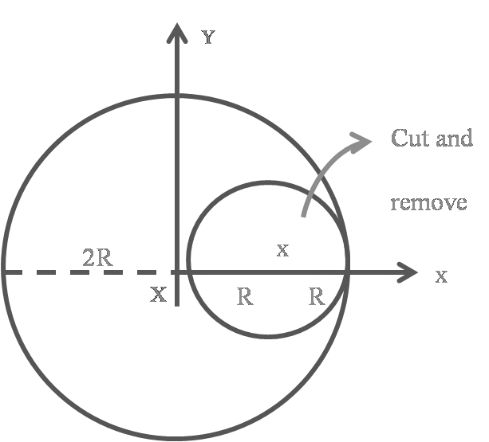
In this case a small disc of radius R is cutting from a large disc of radius 2R. Now finding C.M. of remaining part of the disc

So CM is located at left side form origin at distance R/3

Concep.3 Motion of CM

Concept 4. Shifting of C. M.

Example

Given if 2 kg block displace by 4 meter due right and 8 kg block displace by 2 meter due left then changing in position of C.M.

So C.M. will shift by 0.2 meter due left side

Example:

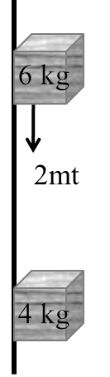
If 6 kg block moves towards down ward by 2 meter and if CM is to be Shift by +3 met in upward direction then amount and direction to which we have to shift 4 kg block.

D Y_cm = + 3 mt

30 = - 12 + 4 DY₂

Concept: 5 If F_ext= 0 then C.M. will not move

Example: Given a boat of mass 50 kg is stationary on a lake. Two Person A and B are initially at two ends of the boat. Now both start to move towards each other and reach the center of the boat. So what will be the distance and direction boat will move.

Solution

(x_cm)_f = 7.5 mt,

Boat displace

(x_cm)_f – (x_cm)_i

= 7.5 - 6.5

= 1 met

Boat will move due left by 1 meter

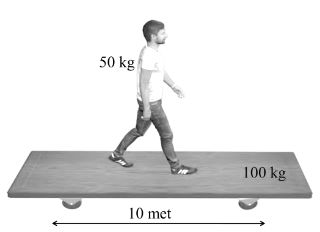
Example: A trolley of mass 100 kg, length 10 mt along with a person of mass 50 kg is initially at rest. But now person moves towards other end of the trolley and reach to other end of the trolley. During this process distance with respect to ground moved by person and trolley. Here we are assuming that trolley is on the smooth surface.

Solution

Trolly will move by (x_cm)_f– (x_cm)_i

6.6 – 3.3

≈ 3.3 met due left side

CONCEPT .6 ACCELERATION OF CM

Example

Finding a_cm = ?

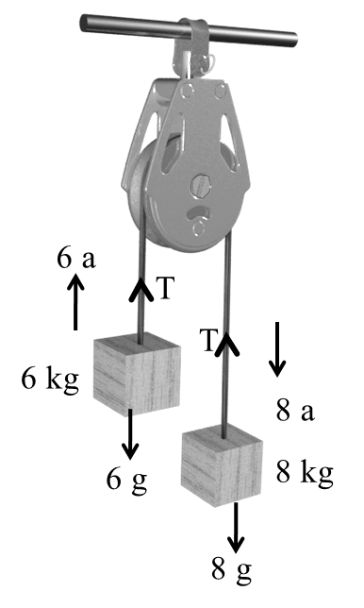
8g - T = 8a

T - 6g = 6 a

2g = 14 a

= -

a_cm = - 0.2 m/s²

A uniform bar of length 12 L and mass 48 m is supported horizontally on two fixed smooth tables as shown in figure. A small moth (an insect) of mass 8m is sitting on end A of the rod and a spider (an insect) of mass 16 m is sitting on the other end. B. Both the insects moving towards each other along the rod with moving at speed 2v and then spider at half this speed (absolute). They met at appoint P on the rod and the spider eats the moth. After this the spider moves with a velocity relative the end A. The spider takes negligible time in eating on the other . Also, let where T is a having value 4s.

Question. Displacement of the rod by the time the insect meet the moth is

(b) L

(d) zero

Solution: p_i = p_f

0 = (8m) (2v) – (16m) (v) + (48m) v’

Here v’ = absolute speed of rod

= 0

Displacement of rod = 0 Answer (d)

Question.. The point P is at

(a) The center of the rod

(b) The edge of the table supporting the end B

(c) The edge of the table supporting end A

(d) None of the above

Solution:

x_A + x_B = 12 L

2vt + vt = 12 L

vt = 4L

Þ X_B = vt = 4L

Question. The speed of the rod after the spider eats up the moth and moves toward A is

(b) v

(d) 2v

Solution:

Answer (c)

Question.. After starting from end B of the rod the spider reaches the end A at a time

(a) 40 s (b) 30 s

(c) 80 s (d) 10 s

Solution:

But Lv=T=4s

∴ t=80 s

Answer (c)

Question. By what distance the center of mass of the rod shift during this time?

(c) L

Solution: Till t₁, rod is stationary. For time t₂ rod is moving with absolute speed u (= v/6)

Answer (a)

LINEAR MOMENTUM

Direction of Linear momentum will be just same as direction of velocity

Case I Changing of linear momentum

Note: (1) Slope of p - t graph will give us Force (F)

(2) Area under the F - t carve will gives us change in momentum

Impulse FDt =Dp Also we can say impulse is change in momentum

Example: A ball of mass 1 kg drops on the hard floor and ball strikes the floor with 10m/s rebound with same speed also. If ball remains for 0.1 sec in contact with floor. Then find

(i) Magnitude of rate of change of momentum

(ii) Rate of change of magnitude of momentum

Solution: Momentum just before strike the floor p₁ = mv

p₁ = - 1 x10

= - 10 kg mt/sec

Momentum just after strike the floor

p₂ = + mv

= + 1 x10

= 10 kg mt/sec

(i) Magnitude of rate change of momentum

(ii) Rate of change of magnitude of momentum

Þ Magnitude of momentum is not changing only direction of momentum is changing

Þ Therefore Ans-Zero

CHANGING IN MOMENTUM

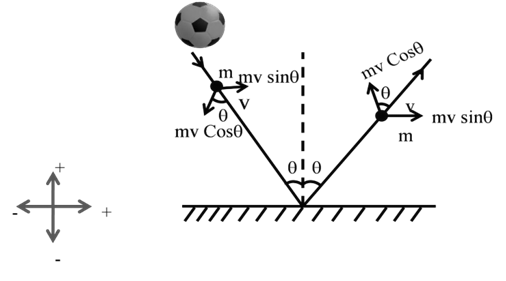
Change in momentum along x- axis Þ

p₁ = mv sinq before Collision

p₂= mv sinq after Collision

(D p_x) = p₂ – p₁ = 0

Change in momentum along y-axis Þ

p₁ = - mv cosq before Collision

p₂ = mv cosq after Collision

(Dp)_y = p₂- p₁ = 2 mv cosq

CHANGING IN MOMENTUM

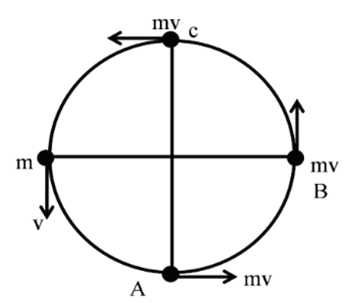
Let assume a ball attached with a string and moving uniformly in a Circular path

(i) Change in momentum from A to B

(ii) Change in momentum from A to C

i

Another case

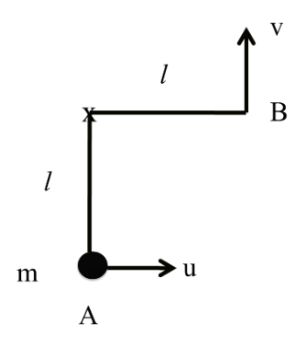
But here

v² = u² – 2gl

Case I Conservation of linear momentum (COLM)

Example:

Given A trolly of mass M kept at rest on a Smooth road. Two person each of mass m Standing at two ends of trolly. Now person A jumps in horizontal direction form the trolly with speed u (with respect to trolly) and then person B jumps in horizontal direction with speed u (with respect to trolly) in opposite direction. Find final speed of trolly just after both person jumps from the trolly.

Solution

Just before A jumps

p₁ = (2 m + m) x 0 = 0

Just after A jumps

p₂ = mu + (M + m) v₁

Now F_ext = 0, applying COLM

p₁ = p₂ Þ mu + (M + m) v₁ = 0

Again if we assume that trolly and person B is at rest

Just before B jumps

p₁ = (M + m) x 0 (Assume)

Just after B jumps

p₂ = - mu + Mv₂

Now applying COLM

p₁ = p₂Þ - mu + Mv₂ = 0

Now Final speed of trolly after both A & B Jumps

V_f = V₁ + V₂

COLLISION

Head on Collision

OBLIQUE COLLISION

Types of Collisions

(1) Perfect elastic Collision.

Momentum will Conserved p₁ = p₂

Energy will Conserved k₁ = k₂

No loss of energy

Coefficient of restitution e = 1

CONCEPT OF EXCHANGE

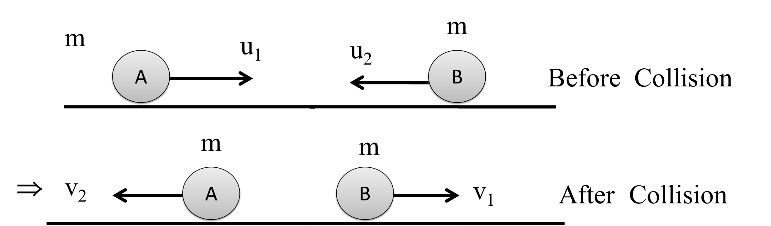
(2) Elastic Collision

Momentum will Conserved p₁ = p₂

Energy will not Conserved k₁¹ k₂

Minimum energy loss Coefficient of restitution

e < 1 (But here e will be Close to 1)

(3) Perfect inelastic Collision

Momentum will conserved p₁ = p₂

Energy will not conserved k₁ ≠ k₂

Maximum energy loss coefficient of restitution e = 0

(4) Inelastic Collision

Momentum will Conserved p₁ = p₂

Energy will not Conserved k₁ ¹ k₂

Maximum energy loss Coefficient of restitution

e > 0 (But here e will be close to 0)

NEWTONS LAW FOR COLLISION

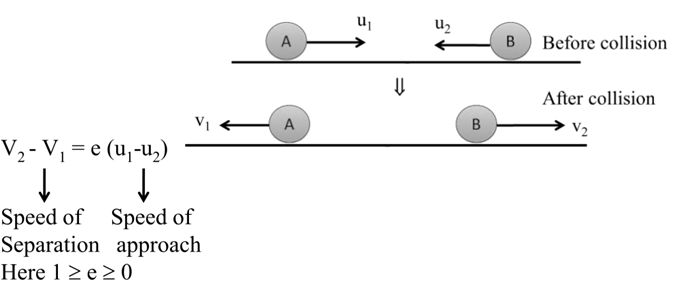
Speed just after Collision = e (Speed just before Collision)

Height after Collision = e² (Height before Collision)

Total distance Covered by the ball

H = h + 2 e² h + 2e⁴ h + -------

= h [ 1 + 2e² (1 + e² + e⁴ + ----)]

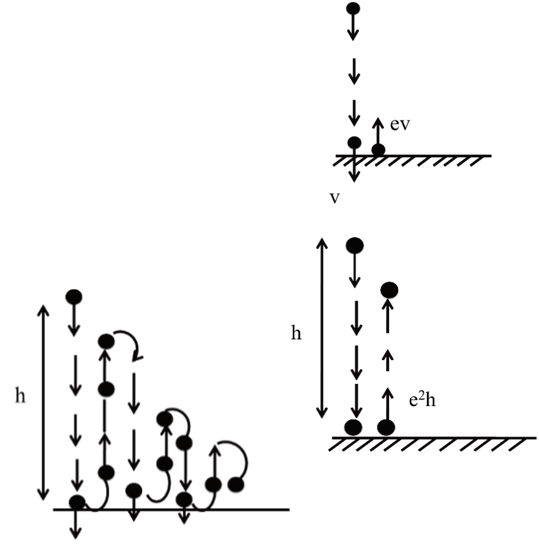
VARIABLE MASS

Case 1

Rocket Propulsion

Thrust force on the rocket in upwards direction

Weight of rocket = mg down ward direction

If gravity (g) neglected and

u = 0 then

Case 2

Density of liquid = P Orifice area = A

A piece of wood of mass 0.03 kg is dropped from the top of a 100 m height building. At the same time, a bullet of mass 0.02 kg is fired vertically upward with velocity 100 ms^-1 from the ground. The bullet gets embedded in the wood. Then, the maximum height to which the combined system reaches above the top of the building before falling below is (take, g = 10 ms^-2) (2019 JEE Main, 10 Jan I)

(a) 20 m (b) 30 m

(c) 10 m (d) 40 m

Solution: Key Idea As bullet gets embedded in the block of wood so, it represents a collision which is perfectly inelastic and hence only momentum of the system is conserved.

Velocity of bullet is very high compared to velocity of wooden block so, in order to calculate time for collision, we take relative velocity nearly equal to velocity of bullet.

So, time taken for particles to collide is

Speed of block just before collision is

v₁ = gt = 10 x 1 = 10 ms^-1

Speed of bullet just before collisions is

v₂ = u – gt

= 100-10 x 1 = 90 ms^-1

Let v = velocity of bullet + block system, then by conservation of linear momentum, we get

- (0.03 x 10) + (0.02 x 90) = (0.05)v

Þ v = 30 ms^-1

Now, maximum height reached by bullet and block is

Þ h = 45 m

Height covered by the system from point of collision = 45 m

Now, distance covered by bullet before collision in 1 sec.

Distance of point of collision from the top of the building = 100 – 95 = 5m

Maximum height to which the combined system reaches above the top of the building before falling below = 45 – 5 = 40 m

Answer (d)

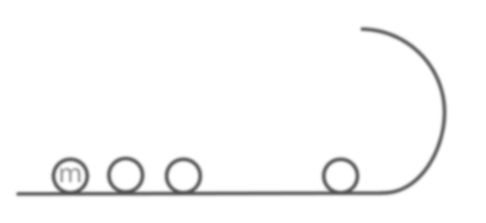
Question. n elastic balls are placed at rest on a smooth horizontal plane which is circular at the ends with radius r as shown in the figure. The masses of the ball are respectively. What is the minimum velocity which should be imparted to the first ball of mass m such that n^th ball completes the vertical circle