Kaysons Publication
1-D MOTION
2-D MOTION OR MOTION IN A PLANE Þ
Motion of any object in any of two axis involve (xy or yz or zx)
“Projectile Motion may be 2-D or even 3-D also but in general it is use to be 2-D Motion”
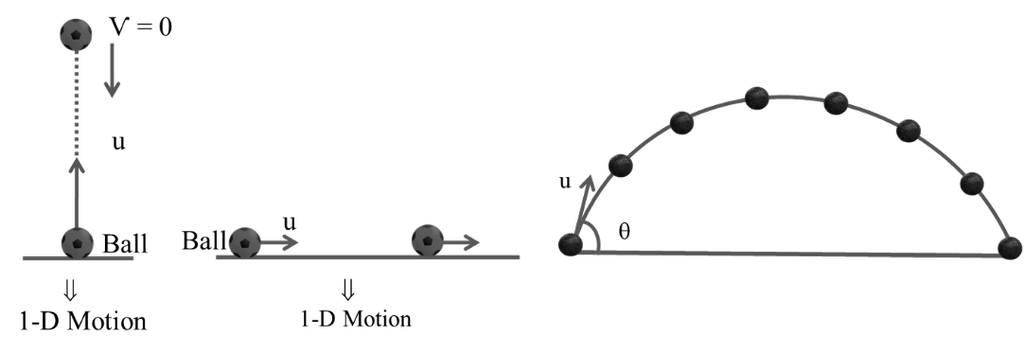
-D PROJECTILE MOTION
VERTICAL MIRROR
Vertical Mirror ® Gravity acts in vertical direction so we can use equations of motion
Time taken by the image of ball going up = time taken going down = t (Let)
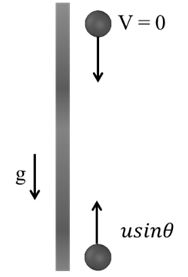
Use v = u – g t
O = u sinq - g t
Total time
Now to get Maximum height
Using v2 = u2 – 2g h
(O)2 = (usinq)2 – 2g H
HORIZONTAL MIRROR
Velocity remains constant so we can not use equation of Motion
Note: Untill any external reason present to change ucosq, like air flow ucosq remains Constant
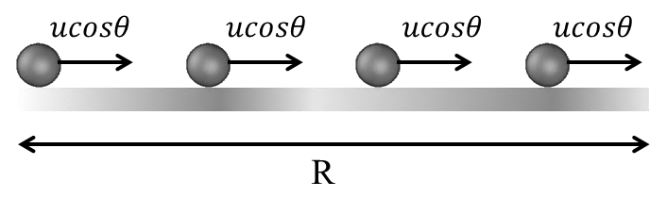
Now ucosq = Const
R = (u cosq) T
Now Sin2q = 2 sinq Cosq
Now we have
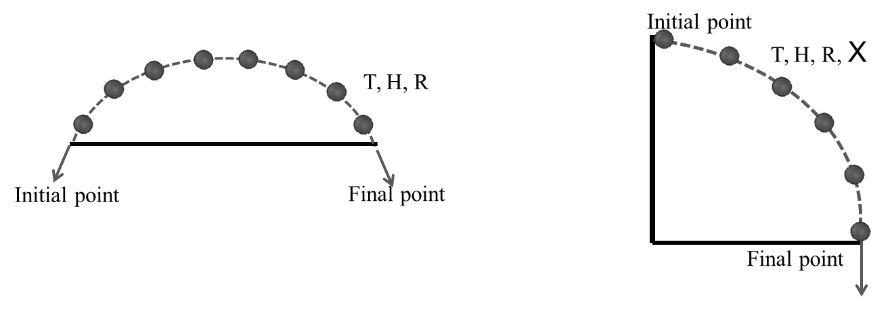
CONDITION
“These three results only when can be use if initial point of projection and final point of projection are at same level.
Example: A body of mass m is projected upward with initial velocity
then find time of flight, Maximum height attained and range attained by the body (g = 10m/s2)
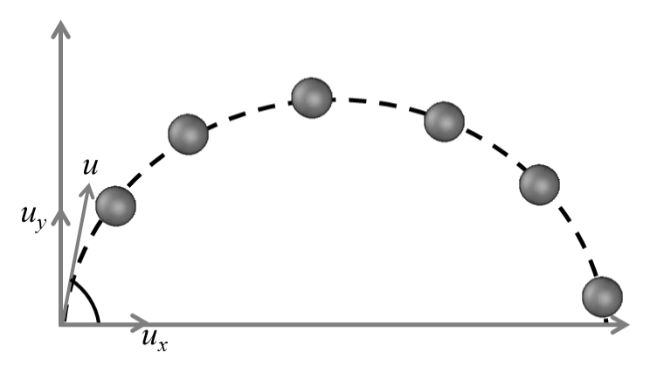
Solution
Maximum range: To get maximum horizontal distance covered by any mass in projectile motion we must have a unique specified angle.
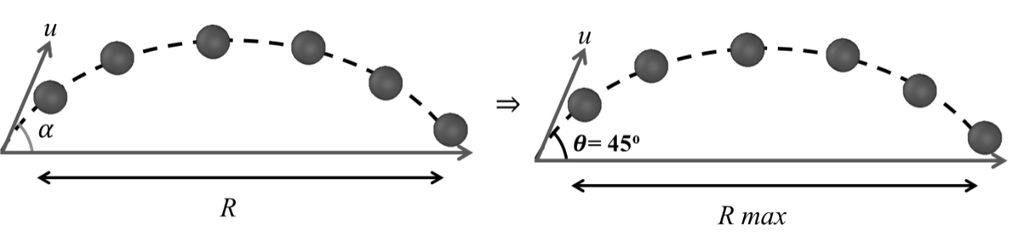
(Sin2q)max = 1
2q = 90°
q = 45°
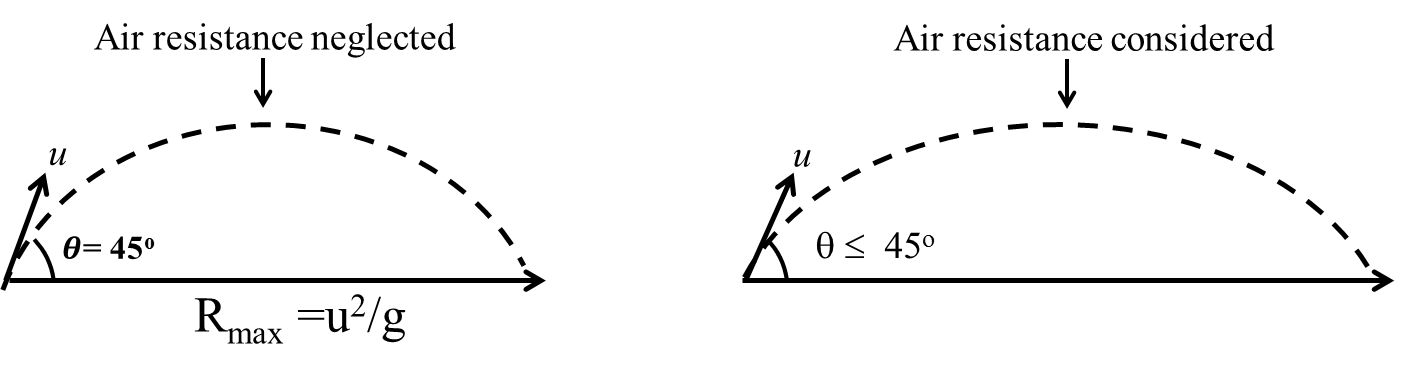
To get maximum range angle of projection should be 45 °,
Note: Here we are neglecting the effect of air resistance. If we Consider air resistance then this angle q should be little bit less than 45°
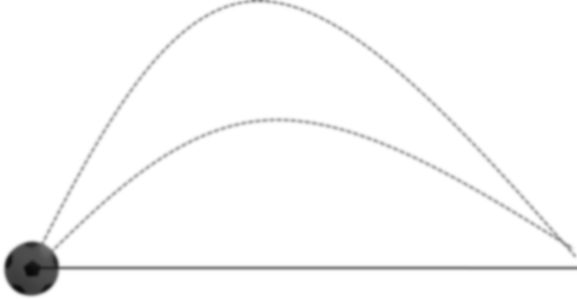
SAME RANGE
Mathematically there must be two different angle of projection for which we will get same range
Ball 1
Ball 2
Now if we assume
a + b = 90°
then b = 90° - a
If sum of angle of projection is = 90° and initial speed is same then both balls will have same range.
Note: Here in this Case only range will be same not time of flight and maximum height
R1 = R2
T1 ¹ T2
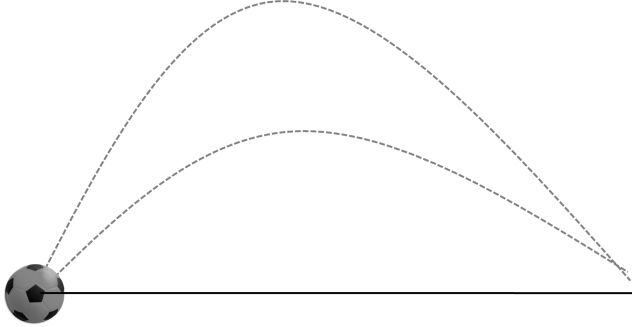
H1 ¹ H2
In case of same range relation of time of flights
Here we know a + b = 90°
Ball 1
Ball 2
Now
In case of same range relation of maximum heights
Here again a +b = 90°
Ball 1
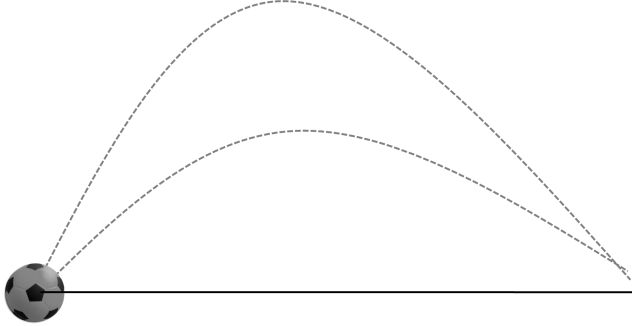
Ball 2
=
