Trigonometric Ratios

Chapter:- 8

Introduction to trigonometry

Introduction

Suppose the students of a school are visiting Qutub Minar. Now, if a student is looking at the top of the Minar, a right triangle can be imagined to be made, as shown in Fig. Can the student find out the height of the Minar, without actually measuring it?

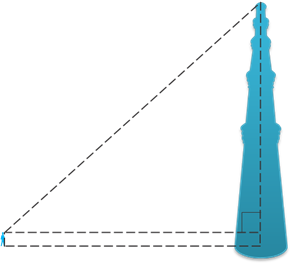
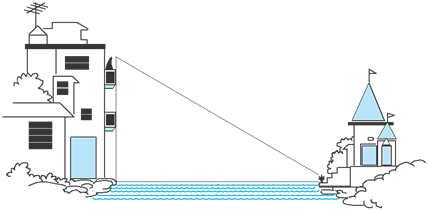
Suppose a girl is sitting on the balcony of her house located on the bank of a river. She is looking down at a flower pot placed on a stair of a temple situated nearby on the other bank of the river. A right triangle is imagined to be made in this situation as shown in Fig. If you know the height at which the person is sitting, can you find the width of the river?

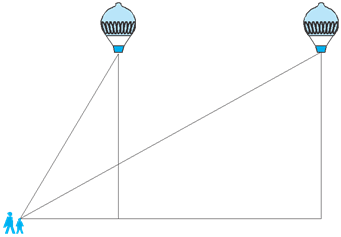
Suppose a hot air balloon is flying in the air. A girl happens to spot the balloon in the sky and runs to her mother to tell her about it. Her mother rushes out of the house to look at the balloon.Now when the girl had spotted the balloon intially it was at point A. When both the mother and daughter came out to see it, it had already travelled to another point B. Can you find the altitude of B from the ground? 

In all the situations given above, the distances or heights can be found by using some mathematical techniques, which come under a branch of mathematics called ‘trigonometry’. The word ‘trigonometry’ is derived from the Greek words ‘tri’ (meaning three), ‘gon’ (meaning sides) and ‘metron’ (meaning measure). In fact, trigonometry is the study of relationships between the sides and angles of a triangle. The earliest known work on trigonometry was recorded in Egypt and Babylon. Early astronomers used it to find out the distances of the stars and planets from the Earth. Even today, most of the technologically advanced methods used in Engineering and Physical Sciences are based on trigonometrical concepts.

In this chapter, we will study some ratios of the sides of a right triangle with respect to its acute angles, called trigonometric ratios of the angle. We will restrict our discussion to acute angles only. However, these ratios can be extended to other angles also. We will also define the trigonometric ratios for angles of measure 0° and 90°. We will calculate trigonometric ratios for some specific angles and establish some identities involving these ratios, called trigonometric identities.

Trigonometric Ratios

In Section 8.1, you have seen some right triangles imagined to be formed in different situations.
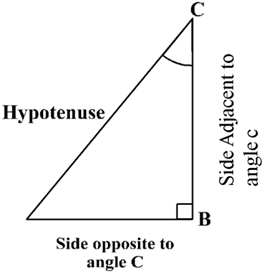
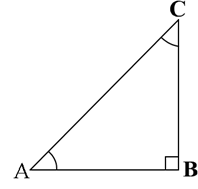
Let us take a right triangle ABC as shown in Fig.
Here, ∠CAB (or, in brief, angle A) is an acute angle. Note the position of the side BC with respect to angle A. it faces ∠A. we call it the side opposite to angle A. AC is the hypotenuse of the right triangle and the side AB is a part of ∠A. so, we call it the side adjacent to angle A.
 

Note that the position of sides change when you consider angle C in place of A.
You have studied the concept of ‘ratio’ in your earlier classes. We now define certain ratios involving the sides of a right triangle, and call them trigonometric ratios.
The trigonometric ratios of the angle A in right triangle ABC are defined as follows:

Sine of      

 

 

 

 

 

The ratios defined above are abbreviated as sin A, cos A, tan A, cosec A, sec A and cot A respectively. Note that the ratios cosec A, sec A and cot A are respectively, the reciprocals of the ratios sin A, cos A and tan A.

Also, observe that tan A =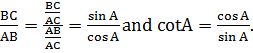 

From our observations, it is now clear that the values of the trigonometric ratios of an angle do not vary with the lengths of the sides of the triangle, if the angle  remains the same.

Trigonometric Ratios of Some Specific Angles

From geometry, you are already familiar with the construction of angles of 30°, 45°, 60° and 90°. In this section, we will find the values of the trigonometric ratios for these angles and, of course, for 0°.

Trigonometric Ratios of 45°
In  ∆ABC, right-angled at B, if one angle is 45°, then the other angle is also 45°, i.e., ∠A =  ∠C = 45°
So,    BC = AB      (Why?)
Now, Suppose BC = AB = a.
Then by Pythagoras Theorem, AC² = AB² + BC² = a² + a² = 2a²,And, therefore,  AC = a  .
Using the definitions of the trigonometric ratios, we have:

  

 

 

 

Trigonometric Ratios of 30° and 60°
Let us now calculate the trigonometric ratios of 30° and 60°. Consider an equilateral triangle ABC. Since each angle in an equilateral triangle is 60°, therefore,
∠A = ∠B = ∠C = 60^o
Draw the perpendicular AD from A to the side BC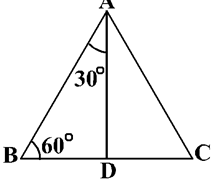  
Now                                ∆ABD ≅ ∆ACD (Why?)
Therefore,                              BD = DC
And                                      ∠BAD = ∠CAD (CPCT)
Now observe that:
∆ABD is a right triangle, right-angled at D with ∠BAD = 30^o and ∠ABD = 60^o
As you know, for finding the trigonometric ratios, we need to know the lengths of the sides of the triangle. So, let us suppose that AB = 2a.

Then,                      
Now, we have:

 

       
Similarly,
 
 

Trigonometric Ratios of 0° and 90°
Let us see what happens to the trigonometric ratios of angle A, if it is made smaller and smaller in the right triangle ABC (see Fig.), till it becomes zero. As ∠A gets smaller and smaller, the length of the side BC decreases. The point C gets closer to point B, and finally when ∠A becomes very close to 0°, AC becomes almost the same as AB.

When ∠A is very close to 0^o, BC gets very close to 0 and so the value of    is very close to 0. Also, when ∠A is very close to 0⁰, AC is nearly the same as AB and so the value of cosA=ABAC is very close to 1. 
This helps us to how we can define the values of sin A cos A when A = 0⁰. We define: sin 0⁰ = 0 and cos 0⁰ = 1.
Using these, we have

 

 
Now, let us see what happens to the trigonometric ratios of ∠A, when it is made larger and larger in ∠ABC till it becomes 90°. As ∠A gets larger and larger, ∠C gets smaller and smaller. Therefore, as in the case above, the length of the side AB goes on decreasing. The point A gets closer to point B. Finally when ∠A is very close to 90°, ∠C becomes very close to 0° and the side AC almost coincides with side BC.

When ∠C is very close to 0^o, ∠A is very close to 90^o, side AC is nearly the same as side BC, and so sin A is very close to 1. Also when ∠A is very close to 90^o, ∠C is very close to 0^o, and the side AB is nearly zero, so cos A is very close to 0.
So, we define:
sin 90^o = 1 and cos 90^o = 0.       
We shall now give the values of all the trigonometric ratios of 0^o, 30^o 45^o, 60^o and 90^o in Table 8.1, for ready reference

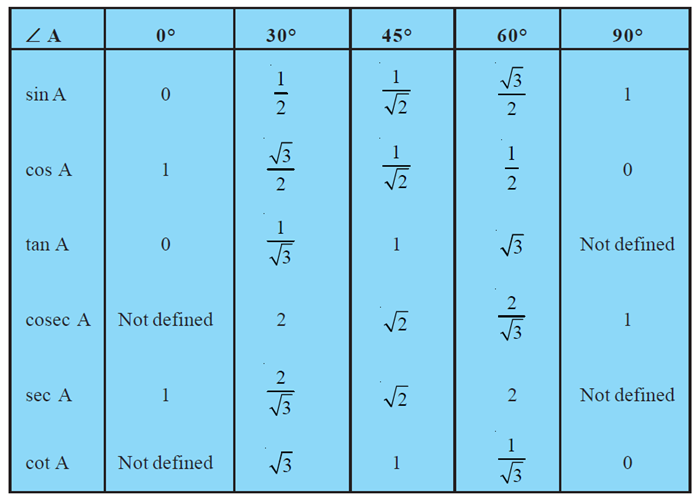
Remark: From the table above you can observe that as ∠A increases from 0^o to 90^o, sin A increases from 0 to 1 and cos A decreases from 1 to 0.

Trigonometric Ratios of Complementary Angles

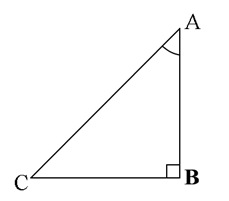
Recall that two angles are said to be complementary if their sum equals 90°. In ∠ABC, right-angled at B, do you see any pair of complementary angles?
Since ∠A + ∠C = 90^o, they form such a pair. We have:

 

 

 

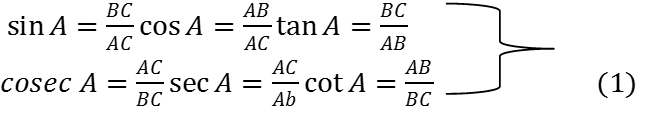
 Now let us write the trigonometric ratios for ∠C = 90^o - ∠A.
For convenience, we shall write 90^o – A instead of 90^o - ∠A.
What would be the side opposite and the side adjacent to the angle 90^o – A?
You will find that AB is the side opposite and BC is the side adjacent to the angle
90^o – A. Therefore,

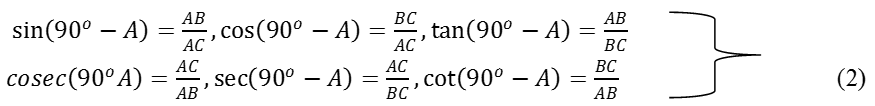
Now, compare the ratios in (1) and (2). Observe that:
 

So,
 
 
 
For all values of angle A lying between 0^o and 90^o. Check whether this holds for     A = 0^o or A = 90^o.

Trigonometric Identities
You may recall that an equation is called an identity when it is true for all values of the variables involved. Similarly, an equation involving trigonometric ratios of an angle is called a trigonometric identity, if it is true for all values of the angle (s) involved.
In this section, we will prove one trigonometric identity, and use it further to prove other useful trigonometric identities.
In ∆ABC, right-angled at B, we have:
AB² + BC² = AC²                           (1)
Dividing each term of (1) by AC², we get
             
i.e.,  
i.e.,                  cos² A + sin² A = 1                         (2)

This is true for all A such that 0^o ≤ A ≤ 90^o. So this is a trigonometric identity.
Let us now divide (1) by AB². We get    

Or,                
i.e.,                           1 + tan² A = sec² A                (3)
Is this equation true for A = 0^o? Yes, it is. What about A = 90^o? Well, tan A and sec A are not defined for A = 90^o. So, (3) is true for all A such that 0^o ≤ A < 90^o.
Let us see what we get on dividing (1) by BC². We get
  
i.e.,   
i.e.,   cot² A + 1 = cosec² A             (4)