Trigonometric Ratios of Some Specific Angles

Trigonometric Ratios of Some Specific Angles

From geometry, you are already familiar with the construction of angles of 30°, 45°, 60° and 90°. In this section, we will find the values of the trigonometric ratios for these angles and, of course, for 0°.

Trigonometric Ratios of 45°
In  ∆ABC, right-angled at B, if one angle is 45°, then the other angle is also 45°, i.e., ∠A =  ∠C = 45°
So,    BC = AB      (Why?)
Now, Suppose BC = AB = a.
Then by Pythagoras Theorem, AC² = AB² + BC² = a² + a² = 2a²,And, therefore,  AC = a  .
Using the definitions of the trigonometric ratios, we have:

Trigonometric Ratios of 30° and 60°
Let us now calculate the trigonometric ratios of 30° and 60°. Consider an equilateral triangle ABC. Since each angle in an equilateral triangle is 60°, therefore,
∠A = ∠B = ∠C = 60^o
Draw the perpendicular AD from A to the side BC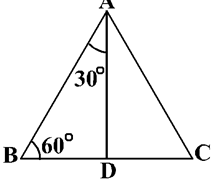  
Now                                ∆ABD ≅ ∆ACD (Why?)
Therefore,                              BD = DC
And                                      ∠BAD = ∠CAD (CPCT)
Now observe that:
∆ABD is a right triangle, right-angled at D with ∠BAD = 30^o and ∠ABD = 60^o
As you know, for finding the trigonometric ratios, we need to know the lengths of the sides of the triangle. So, let us suppose that AB = 2a.

Then,                      
Now, we have:

 

       
Similarly,
 
 

Trigonometric Ratios of 0° and 90°
Let us see what happens to the trigonometric ratios of angle A, if it is made smaller and smaller in the right triangle ABC (see Fig.), till it becomes zero. As ∠A gets smaller and smaller, the length of the side BC decreases. The point C gets closer to point B, and finally when ∠A becomes very close to 0°, AC becomes almost the same as AB.

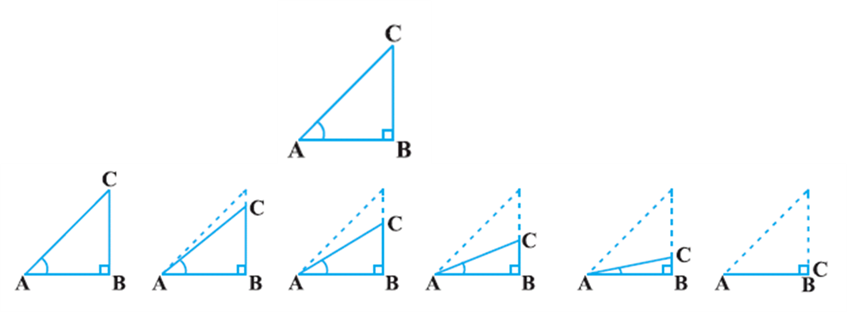
When ∠A is very close to 0^o, BC gets very close to 0 and so the value of    is very close to 0. Also, when ∠A is very close to 0⁰, AC is nearly the same as AB and so the value of cosA=ABAC is very close to 1. 
This helps us to how we can define the values of sin A cos A when A = 0⁰. We define: sin 0⁰ = 0 and cos 0⁰ = 1.
Using these, we have

 
Now, let us see what happens to the trigonometric ratios of ∠A, when it is made larger and larger in ∠ABC till it becomes 90°. As ∠A gets larger and larger, ∠C gets smaller and smaller. Therefore, as in the case above, the length of the side AB goes on decreasing. The point A gets closer to point B. Finally when ∠A is very close to 90°, ∠C becomes very close to 0° and the side AC almost coincides with side BC.

When ∠C is very close to 0^o, ∠A is very close to 90^o, side AC is nearly the same as side BC, and so sin A is very close to 1. Also when ∠A is very close to 90^o, ∠C is very close to 0^o, and the side AB is nearly zero, so cos A is very close to 0.
So, we define:
sin 90^o = 1 and cos 90^o = 0.       
We shall now give the values of all the trigonometric ratios of 0^o, 30^o 45^o, 60^o and 90^o in Table 8.1, for ready reference

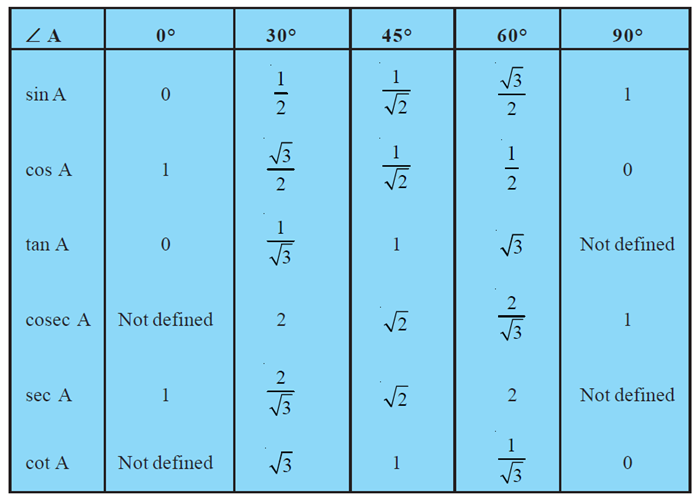
Remark: From the table above you can observe that as ∠A increases from 0^o to 90^o, sin A increases from 0 to 1 and cos A decreases from 1 to 0.