Trigonometric Ratios of Complementary Angles

Trigonometric Ratios of Complementary Angles

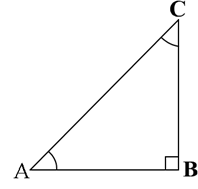
Recall that two angles are said to be complementary if their sum equals 90°. In ∠ABC, right-angled at B, do you see any pair of complementary angles?
Since ∠A + ∠C = 90^o, they form such a pair. We have:

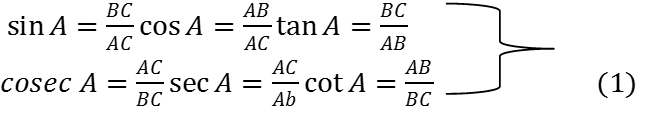
 Now let us write the trigonometric ratios for ∠C = 90^o - ∠A.
For convenience, we shall write 90^o – A instead of 90^o - ∠A.
What would be the side opposite and the side adjacent to the angle 90^o – A?
You will find that AB is the side opposite and BC is the side adjacent to the angle
90^o – A. Therefore,

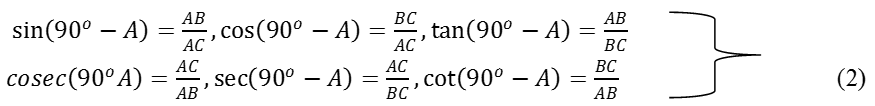
Now, compare the ratios in (1) and (2). Observe that:
 

So,
 
 
 
For all values of angle A lying between 0^o and 90^o. Check whether this holds for     A = 0^o or A = 90^o.

Trigonometric Identities
You may recall that an equation is called an identity when it is true for all values of the variables involved. Similarly, an equation involving trigonometric ratios of an angle is called a trigonometric identity, if it is true for all values of the angle (s) involved.
In this section, we will prove one trigonometric identity, and use it further to prove other useful trigonometric identities.
In ∆ABC, right-angled at B, we have:
AB² + BC² = AC²                           (1)
Dividing each term of (1) by AC², we get
             
i.e.,  
i.e.,                  cos² A + sin² A = 1                         (2)

This is true for all A such that 0^o ≤ A ≤ 90^o. So this is a trigonometric identity.
Let us now divide (1) by AB². We get    

Or,                
i.e.,                           1 + tan² A = sec² A                (3)
Is this equation true for A = 0^o? Yes, it is. What about A = 90^o? Well, tan A and sec A are not defined for A = 90^o. So, (3) is true for all A such that 0^o ≤ A < 90^o.
Let us see what we get on dividing (1) by BC². We get
  
i.e.,   
i.e.,   cot² A + 1 = cosec² A             (4)