TRIANGLES

Chapter -4

TRIANGLES

Introduction

In Class IX, you have seen that all circles with the same radii are congruent, all squares with the same side lengths are congruent and all equilateral triangles with the same side lengths are congruent.
Now consider any two (or more) circles [see Fig (i)]. Are they congruent? Since all of them do not have the same radius, they are not congruent to each other. Note that some are congruent and some are not, but all of them have the same shape. So they all are, what we call, similar. Two similar figures have the same shape but not necessarily the same size. Therefore, all circles are similar. What about two (or more) squares or two (or more) equilateral triangles [see Fig (ii) and (iii)]? As observed in the case of circles, here also all squares are similar and all equilateral triangles are similar.

From the above, we can say that all congruent figures are similar but the similar figures need not be congruent. Can a circle and a square be similar? Can a triangle and a square be similar? These questions can be answered by just looking at the figures (see Fig). Evidently these figures are not similar. (Why?)
What can you say about the two quadrilaterals ABCD and PQRS (see Fig.1)? Are they similar? These figures appear to be similar but we cannot be certain about it. Therefore, we must have some definition of similarity of figures and based on this definition some rules to decide whether the two given figures are similar or not. For this, let us look at the photographs given in Fig. 2:

You will at once say that they are the photographs of the same monument (Taj Mahal) but are in different sizes. Would you say that the three photographs are similar? Yes, they are.
What can you say about the two photographs of the same size of the same person one at the age of 10 years and the other at the age of 40 years? Are these photographs similar? These photographs are of the same size but certainly they are not of the same shape. So, they are not similar.
What does the photographer do when she prints photographs of different sizes from the same negative? You must have heard about the stamp size, passport size and postcard size photographs. She generally takes a photograph on a small size film, say of 35mm size and then enlarges it into a bigger size, say 45mm (or 55mm). Thus, if we consider any line segment in the smaller photograph (figure), its corresponding line segment in the bigger photograph (figure) will be    of that of the line segment. This really means that every line segment of the smaller photograph is enlarged (increased) in the ratio 35:45 (or 35:55). It can also be said that every line segment of the bigger photograph is reduced (decreased) in the ratio 45:35 (or 55:35). Further, if you consider inclinations (or angles) between any pair of corresponding line segments in the two photographs of different sizes, you shall see that these inclinations (or angles) are always equal. This is the essence of the similarity of two figures and in particular of two polygons. We say that:

Similarity of Triangles
You may recall that triangle is also a polygon. So, we can state the same conditions for the similarity of two triangles. That is:
Two triangles are similar, if
(i) Their corresponding angles are equal and
(ii) Their corresponding sides are in the same ratio (or proportion).
Note that if corresponding angles of two triangles are equal, then they are known as equiangular triangles. A famous Greek mathematician Thales gave an important truth relating to two equiangular triangles which is as follows: The ratio of any two corresponding sides in two equiangular triangles is always the same. It is believed that he had used a result called the Basic Proportionality Theorem (now known as the Thales Theorem) for the same.

Theorem: If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
Proof: We are given a triangle ABC in which a line parallel to side BC intersects other two sides AB and AC at D and E respectively (see Fig).

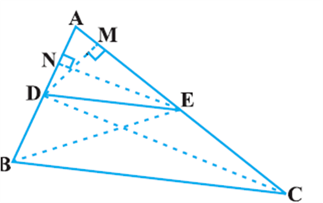
We need to prove that   

Let us join BE and CD and then draw DM ⊥ AC and EN ⊥ AB.
  
Recall from Class IX, that area of ΔADE is denoted as are

  
  
  
  
  
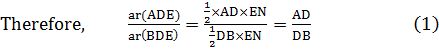
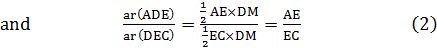
Note that ∆BDE and DEC are on the same base DE and between the same parallels BC and DE.
So,                     ar(BDE) = ar(DEC)
Therefore, from (1), (2) and (3), we have:
                       

Criteria for Similarity of Triangles

In the previous section, we stated that two triangles are similar, if (i) their corresponding angles are equal and (ii) their corresponding sides are in the same ratio (or proportion).
That is, in ΔABC and ΔDEF, if
(i) ∠A = ∠D, ∠B = ∠E, ∠C = ∠F and

 Then the two triangles are similar (see Fig).

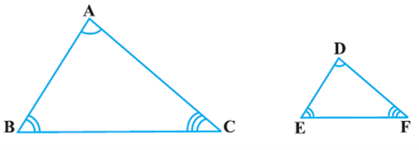
Here, you can see that A corresponds to D, B corresponds to E and C corresponds to F. Symbolically, we write the similarity of these two triangles as ‘ΔABC ~ ΔDEF’ and read it as ‘triangle ABC is similar to triangle DEF’. The symbol ‘~’ stands for ‘is similar to’. Recall that you have used the symbol ‘≅’ for ‘is congruent to’ in Class IX.

Now a natural question arises: For checking the similarity of two triangles, say ABC and DEF, should we always look for all the equality relations of their corresponding angles (∠A = ∠D, ∠B = ∠E, ∠C = ∠F) and all the equality relations of the ratios of their corresponding sides  ? Let us examine. You may recall that in Class IX, you have obtained some criteria for congruency of two triangles involving only three pairs of corresponding parts (or elements) of the two triangles. Here also, let us make an attempt to arrive at certain criteria for similarity of two triangles involving relationship between less numbers of pairs of corresponding parts of the two triangles, instead of all the six pairs of corresponding parts. For this, let us perform the following activity:

Theorem: If in two triangles, sides of one triangle are proportional to (i.e., in the same ratio of) the sides of the other triangle, then their corresponding angles are equal and hence the two triangles are similar. This criterion is referred to as the SSS (Side–Side–Side) similarity criterion for two triangles.

This theorem can be proved by taking two triangles ABC and DEF such that  

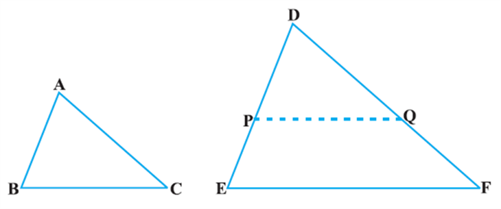
Cut DP = AB and DQ = AC and join PQ.

   

 

 

 

 

 

 

Theorem: If one angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional, then the two triangles are similar. This criterion is referred to as the SAS (Side–Angle–Side) similarity criterion for two triangles.

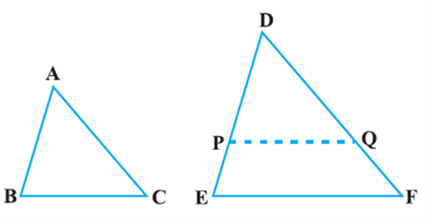
As before, this theorem can be proved by taking two triangles ABC and DEF such that    (see Fig). Cut DP = AB, DQ = AC and join PQ.

Now, PQ || EF and ΔABC ≅ ΔDPQ           (How?)
So, ∠A = ∠D, ∠B = ∠P and ∠C = ∠Q
Therefore, ΔABC ~ ΔDEF                          (Why?)
We now take some examples to illustrate the use of these criteria.
Theorem: The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Proof : We are given two triangles ABC and PQR such that
ΔABC ~ ΔPQR (see Fig).

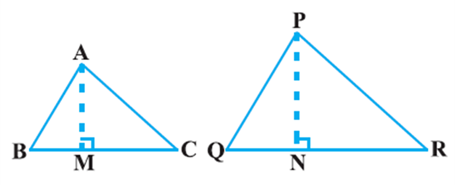
We need to prove that  

For finding the areas of the two triangles, we draw altitudes AM to PN of the triangles.
 
 
 

  

 

 
 
 
  
  
 

Now using (3), we get    
     
Let us take an example to illustrate the use of this theorem.

Pythagoras Theorem
You are already familiar with the Pythagoras Theorem from your earlier classes. You had verified this theorem through some activities and made use of it in solving certain problems. You have also seen a proof of this theorem in Class IX. Now, we shall prove this theorem using the concept of similarity of triangles. In proving this, we shall make use of a result related to similarity of two triangles formed by the perpendicular to the hypotenuse from the opposite vertex of the right triangle.
Now, let us take a right triangle ABC, right angled at B. Let BD be the perpendicular to the hypotenuse AC (see Fig).
 

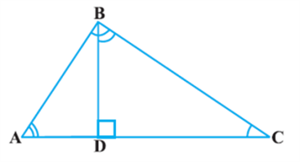
You may note that in ΔADB and ΔABC
                                                 ∠A = ∠A
and                                     ∠ADB = ∠ABC (Why?)
So,                                        ΔADB ~ ΔABC  (How?)                            (1)  
imilarly,                           ΔBDC ~ ΔABC (How?)                                (2)
So, from (1) and (2), triangles on both sides of the perpendicular BD are similar to the whole triangle ABC.
Also, since                   ΔADB ~ ΔABC
and                              ΔBDC ~ ΔABC
So,                     ΔADB ~ ΔBDC        (From Remark in Section 6.2)
The above discussion leads to the following theorem:
Theorem: If a perpendicular is drawn from the vertex of the right angle of a right triangle to the hypotenuse then triangles on both sides of the perpendicular are similar to the whole triangle and to each other.
Let us now apply this theorem in proving the Pythagoras Theorem:

Theorem: In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

Proof: We are given a right triangle ABC right angled at B.  

We need to prove that AC² = AB² + BC²

Let us draw    BD ⊥ AC    (see Fig.)

Now,          ΔADB ~ ΔABC    (Theorem)

 

  

Also,    ΔBDC ~ ΔABC (Theorem)

 

  
Adding (1) and (2),

AD . AC + CD .  AC = AB² + BC²  

or,  AC (AD + CD) = AB² + BC²  

or,  AC . AC = AB² + BC²  

or,  AC² = AB² + BC²  

Theorem: In a triangle, if square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.
Proof: Here, we are given a triangle ABC in which AC² = AB² + BC².
We need to prove that ∠B = 90°.
To start with, we construct a ΔPQR right angled at Q such that PQ = AB and QR = BC (see Fig).

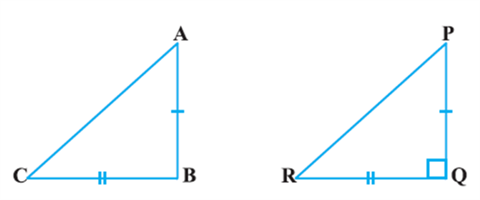
Now, from ΔPQR, we have:

 PR² = PQ² + QR²         (Pythagoras Theorem, as ∠Q = 90°)

or,                PR² = AB² + BC²   (By construction) (1)

But              AC² = AB² + BC²   (Given)                (2)
So,                        AC = PR                [From (1) and (2)] (3)
Now, in ΔABC and ΔPQR,
AB = PQ               (By construction)
BC = QR               (By construction)
AC = PR                [Proved in (3) above]
So,                      ΔABC ≅ ΔPQR                  (SSS congruence)
Therefore,        ∠B = ∠Q                    (CPCT)
But                   ∠Q = 90°          (By construction)
So,                   ∠B = 90°
Note: Also see Appendix 1 for another proof of this theorem.