QUADRATIC EQUATIONS

Chapter-7

Quadratic equations

Introduction
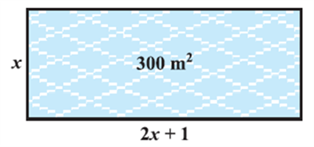
In Chapter 2, you have studied different types of polynomials. One type was the quadratic polynomial of the form ax² + bx + c, a ≠ 0. When we equate this polynomial to zero, we get a quadratic equation. Quadratic equations come up when we deal with many real-life situations. For instance, suppose a charity trust decides to build a prayer hall having a carpet area of 300 square metres with its length one metre more than twice its breadth. What should be the length and breadth of the hall? Suppose the breadth of the hall is x metres. Then, its length should be (2x + 1) metres. We can depict this information pictorially as shown in Fig.
Now,            area of the hall = (2x + 1). xm² = (2x² + x) m²
So,                 2x² + x = 300 (Given)
Therefore,     2x² + x – 300 = 0
So, the breadth of the hall should satisfy the equation 2x² + x – 300 = 0 which is a quadratic equation.

Quadratic Equations
A quadratic equation in the variable x is an equation of the form ax² + bx + c = 0, where a, b, c are real numbers, a ≠ 0. For example, 2x² + x – 300 = 0 is a quadratic equation.
Similarly, 2x² – 3x + 1 = 0, 4x – 3x² + 2 = 0 and 1 – x² + 300 = 0 are also quadratic equations.
In fact, any equation of the form p(x) = 0, where p(x) is a polynomial of degree 2, is a quadratic equation. But when we write the terms of p(x) in descending order of their degrees, then we get the standard form of the equation. That is, ax² + bx + c = 0, a ≠ 0 is called the standard form of a quadratic equation.
Quadratic equations arise in several situations in the world around us and in different fields of mathematics.

Relationship between Zeroes and Coefficients of a Polynomial
In general, a real number α is called a root of the quadratic equation ax² + bx + c = 0, a ≠ 0 if a α² + bα + c = 0. We also say that x = α is a solution of the quadratic equation, or that α satisfies the quadratic equation. Note that the zeroes of the quadratic polynomial ax² + bx + c and the roots of the quadratic equation ax² + bx + c = 0 are the same.
Note:- That we have found the roots of 2x² – 5x + 3 = 0 by factorizing 2x² – 5x + 3 into two linear factors and equating each factor to zero.

Solution of a Quadratic Equation by Completing the Square

In the previous section, you have learnt one method of obtaining the roots of a quadratic equation. In this section, we shall study another method.
Consider the following situation:
The product of Sunita’s age (in years) two years ago and her age four years from now is one more than twice her present age. What is her present age?
To answer this, let her present age (in years) be x. Then the product of her ages two years ago and four years from now is (x – 2) (x + 4).
Now consider the quadratic equation (x + 2)² – 9 = 0. To solve it, we can write it as        (x + 2)² = 9. Taking square roots, we get x + 2 = 3 or x + 2 = – 3.
Therefore,   x = 1 or x = –5
So, the roots of the equation (x + 2)² – 9 = 0 are 1 and – 5.
In both the examples above, the term containing x is completely inside a square, and we found the roots easily by taking the square roots. But, what happens if we are asked to solve the equation x² + 4x – 5 = 0? We would probably apply factorisation to do so, unless we realise (somehow!) that x² + 4x – 5 = (x + 2)² – 9.
So, solving x² + 4x – 5 = 0 is equivalent to solving (x + 2)² – 9 = 0, which we have seen is very quick to do. In fact, we can convert any quadratic equation to the form  (x + a)² – b² = 0 and then we can easily find its roots. Let us see if this is possible.
Look at Fig.
In this figure, we can see how x² + 4x is being converted to (x + 2)² – 4.

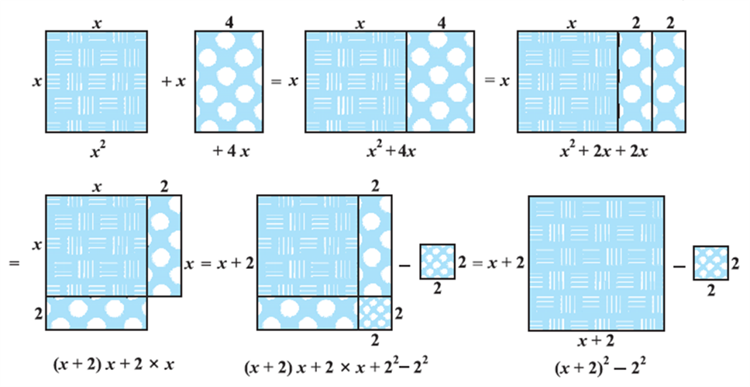
So, x² + 4x – 5 = 0 can be written as (x + 2)² – 9 = 0 by this process of completing the square. This is known as the method of completing the square.

In brief, this can be shown as follows:
 
 
 
 
Consider now the equation 3x² – 5x + 2 = 0. Note that the coefficient of x² is not a perfect square. So, we multiply the equation throughout by 3 to get

 
 
 
   
So, 9x² – 15x + 6 = 0 can be written as
 

So, the solution of 9x² – 15x + 6 = 0 are the same as those of  
 
(We can also write this as  where ‘± ’ denotes minus’.)
 
 
 
Consider the quadratic equation  Dividing throughout by a,
We get     
 
 
So, the roots of the given equation are the same as those of
  

If b²-4ac ≥ 0, then by taking the square in 1, we get  

So, the roots of ax² + bx + c = 0 are   

Equation will have no real roots. (Why?)
Thus, if  then the roots of the quadratic equation ax² + bx + = 0 are given by  
This formula for finding the roots of a quadratic equation is known as the quadratic formula.

Nature of Roots
In the previous section, you have seen that the roots of the equation ax² + bx + c = 0 are given by
    
If b² – 4ac > 0, we get two distinct real roots  

 
So, the roots of the equation ax² + bx + c = 0 are both  
Therefore, we say that the quadratic equation ax² + bx + c = 0 has two equal real roots in this case.
If b² – 4ac < 0, then there is no real number whose square is b² – 4ac. Therefore, there are no real roots for the given quadratic equation in this case.
Since b² – 4ac determines whether the quadratic equation ax² + bx + c = 0 has real roots or not, b² – 4ac is called the discriminant of this quadratic equation.
So, a quadratic equation ax² + bx + c = 0 has
(i) Two distinct real roots, if b² – 4ac > 0,
(ii) Two equal real roots, if b² – 4ac = 0,
(iii) No real roots, if b² – 4ac < 0.