Introduction
- Books Name
- Kaysons Academy Maths Foundation Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Maths
Chapter-7
Quadratic equations
Introduction
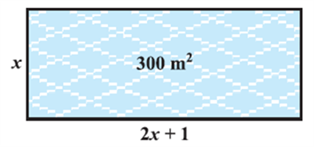
In Chapter 2, you have studied different types of polynomials. One type was the quadratic polynomial of the form ax2 + bx + c, a ≠ 0. When we equate this polynomial to zero, we get a quadratic equation. Quadratic equations come up when we deal with many real-life situations. For instance, suppose a charity trust decides to build a prayer hall having a carpet area of 300 square metres with its length one metre more than twice its breadth. What should be the length and breadth of the hall? Suppose the breadth of the hall is x metres. Then, its length should be (2x + 1) metres. We can depict this information pictorially as shown in Fig.
Now, area of the hall = (2x + 1). xm2 = (2x2 + x) m2
So, 2x2 + x = 300 (Given)
Therefore, 2x2 + x – 300 = 0
So, the breadth of the hall should satisfy the equation 2x2 + x – 300 = 0 which is a quadratic equation.
Quadratic Equations
A quadratic equation in the variable x is an equation of the form ax2 + bx + c = 0, where a, b, c are real numbers, a ≠ 0. For example, 2x2 + x – 300 = 0 is a quadratic equation.
Similarly, 2x2 – 3x + 1 = 0, 4x – 3x2 + 2 = 0 and 1 – x2 + 300 = 0 are also quadratic equations.
In fact, any equation of the form p(x) = 0, where p(x) is a polynomial of degree 2, is a quadratic equation. But when we write the terms of p(x) in descending order of their degrees, then we get the standard form of the equation. That is, ax2 + bx + c = 0, a ≠ 0 is called the standard form of a quadratic equation.
Quadratic equations arise in several situations in the world around us and in different fields of mathematics.
Relationship between Zeroes and Coefficients of a Polynomial
In general, a real number α is called a root of the quadratic equation ax2 + bx + c = 0, a ≠ 0 if a α2 + bα + c = 0. We also say that x = α is a solution of the quadratic equation, or that α satisfies the quadratic equation. Note that the zeroes of the quadratic polynomial ax2 + bx + c and the roots of the quadratic equation ax2 + bx + c = 0 are the same.
Note:- That we have found the roots of 2x2 – 5x + 3 = 0 by factorizing 2x2 – 5x + 3 into two linear factors and equating each factor to zero.
Solution of a Quadratic Equation by Completing the Square
- Books Name
- Kaysons Academy Maths Foundation Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Maths
Solution of a Quadratic Equation by Completing the Square
In the previous section, you have learnt one method of obtaining the roots of a quadratic equation. In this section, we shall study another method.
Consider the following situation:
The product of Sunita’s age (in years) two years ago and her age four years from now is one more than twice her present age. What is her present age?
To answer this, let her present age (in years) be x. Then the product of her ages two years ago and four years from now is (x – 2) (x + 4).
Now consider the quadratic equation (x + 2)2 – 9 = 0. To solve it, we can write it as (x + 2)2 = 9. Taking square roots, we get x + 2 = 3 or x + 2 = – 3.
Therefore, x = 1 or x = –5
So, the roots of the equation (x + 2)2 – 9 = 0 are 1 and – 5.
In both the examples above, the term containing x is completely inside a square, and we found the roots easily by taking the square roots. But, what happens if we are asked to solve the equation x2 + 4x – 5 = 0? We would probably apply factorisation to do so, unless we realise (somehow!) that x2 + 4x – 5 = (x + 2)2 – 9.
So, solving x2 + 4x – 5 = 0 is equivalent to solving (x + 2)2 – 9 = 0, which we have seen is very quick to do. In fact, we can convert any quadratic equation to the form (x + a)2 – b2 = 0 and then we can easily find its roots. Let us see if this is possible.
Look at Fig.
In this figure, we can see how x2 + 4x is being converted to (x + 2)2 – 4.
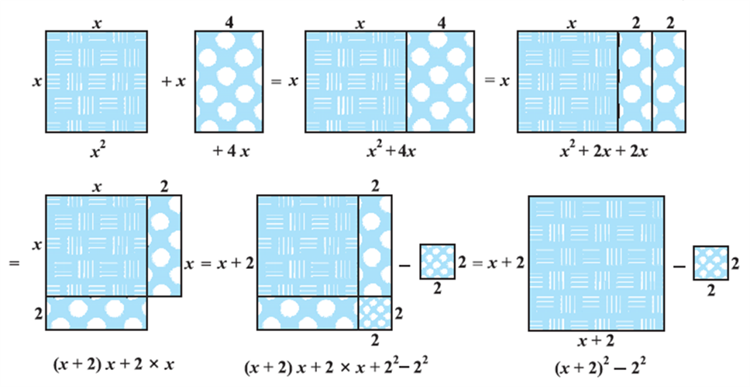
So, x2 + 4x – 5 = 0 can be written as (x + 2)2 – 9 = 0 by this process of completing the square. This is known as the method of completing the square.
In brief, this can be shown as follows:
![]()
![]()
![]()
![]()
Consider now the equation 3x2 – 5x + 2 = 0. Note that the coefficient of x2 is not a perfect square. So, we multiply the equation throughout by 3 to get
![]()
![]()
![]()
![]()
So, 9x2 – 15x + 6 = 0 can be written as
![]()
![]()
So, the solution of 9x2 – 15x + 6 = 0 are the same as those of ![]()
![]()
(We can also write this as ![]() where ‘
where ‘
![]()
![]()
![]()
Consider the quadratic equation ![]() Dividing throughout by a,
Dividing throughout by a,
We get ![]()
![]()
![]()
So, the roots of the given equation are the same as those of
![]()
![]()
![]()
So, the roots of ax2 + bx + c = 0 are ![]()
Equation will have no real roots. (Why?)
Thus, if ![]() then the roots of the quadratic equation ax2 + bx + = 0 are given by
then the roots of the quadratic equation ax2 + bx + = 0 are given by ![]()
This formula for finding the roots of a quadratic equation is known as the quadratic formula.
Nature of Roots
In the previous section, you have seen that the roots of the equation ax2 + bx + c = 0 are given by
![]()
If b2 – 4ac > 0, we get two distinct real roots ![]()
![]()
So, the roots of the equation ax2 + bx + c = 0 are both ![]()
Therefore, we say that the quadratic equation ax2 + bx + c = 0 has two equal real roots in this case.
If b2 – 4ac < 0, then there is no real number whose square is b2 – 4ac. Therefore, there are no real roots for the given quadratic equation in this case.
Since b2 – 4ac determines whether the quadratic equation ax2 + bx + c = 0 has real roots or not, b2 – 4ac is called the discriminant of this quadratic equation.
So, a quadratic equation ax2 + bx + c = 0 has
(i) Two distinct real roots, if b2 – 4ac > 0,
(ii) Two equal real roots, if b2 – 4ac = 0,
(iii) No real roots, if b2 – 4ac < 0.

 Kaysons Publication
Kaysons Publication
