PAIR OF LINEAR EQUATIONS IN TWO VARIABLES

Chapter -3

Pair of Linear Equations in Two Variables

Pair of Linear Equations in Two Variables
Recall, from Class IX, that the following are examples of linear equations in two variables:
2x + 3y = 5
x – 2y – 3 = 0
and    x – 0y = 2,  i.e.,  x = 2s
You also know that an equation which can be put in the form ax + by + c = 0, where a, b and c are real numbers, and a and b are not both zero, is called a linear equation in two variables x and y. (We often denote the condition a and b are not both zero by a₂ + b₂ ≠ 0). You have also studied that a solution of such an equation is a pair of values, one for x and the other for y, which makes the two sides of the equation equal.
For example, let us substitute x = 1 and y = 1 in the left hand side (LHS) of the equation 2x + 3y = 5. Then
LHS = 2(1) + 3(1) = 2 + 3 = 5,
which is equal to the right hand side (RHS) of the equation. Therefore, x = 1 and y = 1 is a solution of the equation 2x + 3y = 5. Now let us substitute x = 1 and y = 7 in the equation 2x + 3y = 5. Then,
LHS = 2(1) + 3(7) = 2 + 21 = 23 which is not equal to the RHS.
Therefore, x = 1 and y = 7 is not a solution of the equation.
Geometrically, what does this mean? It means that the point (1, 1) lies on the line representing the equation 2x + 3y = 5, and the point (1, 7) does not lie on it. So, every solution of the equation is a point on the line representing it.
In fact, this is true for any linear equation, that is, each solution (x, y) of a linear equation in two variables, ax + by + c = 0, corresponds to a point on the line representing the equation, and vice versa.
Now, consider Equations (1) and (2) given above. These equations, taken together, represent the information we have about Akhila at the fair.
These two linear equations are in the same two variables x and y. Equations like these are called a pair of linear equations in two variables.

Graphical Method of Solution of a Pair of Linear Equations
In the previous section, you have seen how we can graphically represent a pair of linear equations as two lines. You have also seen that the lines may intersect, or may be parallel, or may coincide. Can we solve them in each case? And if so, how? We shall try and answer these questions from the geometrical point of view in this section.
Let us look at the earlier examples one by one.
l In the situation of Example 1, find out how many rides on the Giant Wheel Akhila had, and how many times she played Hoopla.
In Fig. 3.2, you noted that the equations representing the situation are geometrically shown by two lines intersecting at the point (4, 2). Therefore, the point (4, 2) lies on the lines represented by both the equations x – 2y = 0 and 3x + 4y = 20. And this is the only common point.
Let us verify algebraically that x = 4, y = 2 is a solution of the given pair of equations. Substituting the values of x and y in each equation, we get
4 – 2 × 2 = 0 and 3(4) + 4(2) = 20. So, we have verified that x = 4, y = 2 is a solution of both the equations. Since (4, 2) is the only common point on both the lines, there is one and only one solution for this pair of linear equations in two variables.
We can now summarise the behavior of lines representing a pair of linear equations in two variables and the existence of solutions as follows:
(i)  The lines may intersect in a single point. In this case, the pair of equations has a unique solution (consistent pair of equations).
(ii)  The lines may be parallel. In this case, the equations have no solution (Inconsistent pair of equations).
(iii)  The lines may be coincident. In this case, the equations have infinitely many solutions [dependent (consistent) pair of equations].
Let us now go back to the pairs of linear equations formed in Examples 1, 2, and 3, and note down what kind of pair they are geometrically.

(i) x – 2y = 0 and 3x + 4y – 20 = 0                   (The lines intersect)
(ii) 2x + 3y – 9 = 0 and 4x + 6y – 18 = 0        (The lines coincide)
(iii)  x + 2y – 4 = 0 and 2x + 4y – 12 = 0       (The lines are parallel)

Algebraic Methods of Solving a Pair of Linear Equations

In the previous section, we discussed how to solve a pair of linear equations graphically. The graphical method is not convenient in cases when the point representing the solution of the linear equations has non-integral coordinates like  etc. There is every possibility of making mistakes while reading such coordinates. Is there any alternative method of finding the solution? There are several algebraic methods, which we shall now discuss.

Substitution Method: We shall explain the method of substitution by taking some examples.

Example: Solve the following pair of equations by substitution method:

7x – 15y = 2                                                           (1)
           x + 2y = 3                                                              (2)

Solution:

Step 1: We pick either of the equations and write one variable in terms of the other. Let us consider the Equation (2):

x + 2y = 3

and write it as       x = 3 – 2y                                                    (3)

Step 2: Substitute the value of x in Equation (1). We get
7(3 – 2y) – 15y = 2
i.e.,                 21 – 14y – 15y = 2
i.e.,                           – 29y = –19
Therefore,         
Step 3: Substituting this value of y in Equation (3), we get  

Therefore, the solution is 

Verification: Substituting x = 29 and y = 29, you can verify that both the Equations
(1) and (2) are satisfied.
Remark: We have substituted the value of one variable by expressing it in terms of the other variable to solve the pair of linear equations. That is why the method is known as the substitution method.

Elimination Method
Now let us consider another method of eliminating (i.e., removing) one variable. This is sometimes more convenient than the substitution method. Let us see how this method works.

Cross - Multiplication Method
So far, you have learnt how to solve a pair of linear equations in two variables by graphical, substitution and elimination methods. Here, we introduce one more algebraic method to solve a pair of linear equations which for many reasons is a very useful method of solving these equations. Before we proceed further, let us consider the following situation.
Let us now see how this method works for any pair of linear equations in two variables of the form

            a₁x + b₁y + c₁ = 0                                                             (1)

and               a₂x + b₂y + c₂ = 0                                                             (2)

To obtain the values of x and y as shown above, we follow the following steps:

Step 1: Multiply Equation (1) by b₂ and Equation (2) by b₁, to get

b₂a₁x + b₂b₁y + b₂c₁ = 0                                                (3)

b₁a₂x + b₁b₂y + b₁c₂ = 0                                                (4)

Step 2: Subtracting Equation (4) from (3), we get:

(b₂a₁ – b₁a₂) x + (b₂b₁ – b₁b₂) y + (b₂c₁ – b₁c₂) = 0

i.e.,    (b₂a₁ – b₁a₂) x = b₁c₂ – b₂c₁

     (5)

 Step 3: Substituting this value of x in (1) or (2), we get

                                                            (6)

Now, two cases arise:
Case 1:  a₁b₂ – a₂b₁ ≠ 0. In this case  Then the pair of linear equations has a unique solution.
Case 2: a₁b₂ – a₂b₁ = 0. If we write

  then a₁ = k a₂, b₁ = k b₂.
Substituting the values of a₁ and b₁ in the Equation (1), we get
                       k(a₂x + b₂y) + c₁ = 0.                                                           (7)
It can be observed that the Equations (7) and (2) can both be satisfied only if

 c₁ = k c₂, i.e.,
If c₁ = k c₂, any solution of Equation (2) will satisfy the Equation (1), and vice versa. So, if   , then there are infinitely many solutions to the pair of linear equations given by (1) and (2).
If c₁ ≠ k c₂, then any solution of Equation (1) will not satisfy Equation (2) and vice versa. Therefore the pair has no solution.
We can summarise the discussion above for the pair of linear equations given by (1) and (2) as follows:

(i) When  we get a unique solution.

(ii) When   there are infinitely many solutions.

(iii) When    there is no solution.

Note that you can write the solution given by Equations (5) and (6) in the following form:

                                                         (8)

In remembering the above result, the following diagram may be helpful to you:

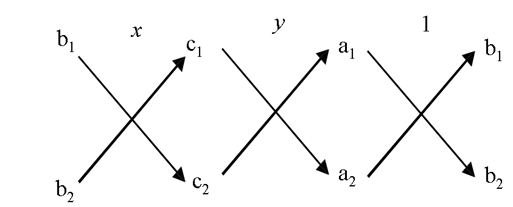
The arrows between the two numbers indicate that they are to be multiplied and the second product is to be subtracted from the first.
For solving a pair of linear equations by this method, we will follow the following steps:
Step 1: Write the given equations in the form (1) and (2).
Step 2: Taking the help of the diagram above, write Equations as given in (8).
Step 3: Find x and y, provided a₁b₂ – a₁b₁ ≠ 0
Step 2 above gives you an indication of why this method is called the cross-multiplication method.

Equations Reducible to a Pair of Linear Equations in Two Variables
In this section, we shall discuss the solution of such pairs of equations which are not linear but can be reduced to linear form by making some suitable substitutions. We now explain this process through some examples.